６．１次元剛体棒流体の構造因子

ここまで１次元剛体棒流体の構造を眺めてきました。 Zernicke と Prins は導出した１次元剛体棒流体の構造を手がかりに、 液体のＸ線（レントゲン線）構造解析の理論的な枠組みを構成することに成功しました。 Zernicke と Prins の論文はそれ故に名高いわけですが、 ここでは特に１次元の流体に関わる範囲で、彼らの取り扱いを跡付けておこうと思います。

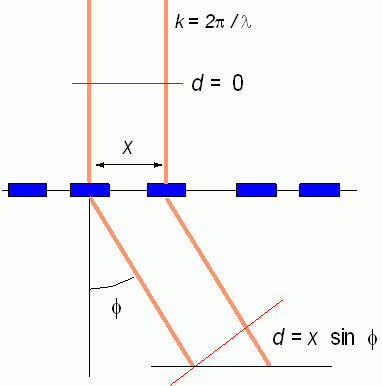
Zernicke と Prins は、平面回折格子を考え、回折格子の１本１本の線同士が、 あたかも剛体棒分子のように振舞って配置したと考えた時の、Ｘ線の回折強度について考えました。 図に示すように、Ｘ線は回折格子に対して垂直に入射してくるものとします。 距離 x 離れた格子線から角度 ϕ 回折されて出てくるＸ線は、 x sin ϕ だけの光路差 d を持つことになります。

さて回折されて出てくる角振動数ωのＸ線の電場の振動を、下式のように表しましょう。 ここで k は 2π/λ で、d_m は回折格子の m 本目の線からの回折Ｘ線の光路差です （Zernike-Prins は 2π/λ のままで表記していますが、簡単のためこれを k とおいておきます）。

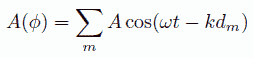　　(6.1)

回折Ｘ線の強さは、電場の２乗で評価されますから、 電場の２乗の時間平均をとって、回折Ｘ線強度 I(ϕ) は次式のように書けます：

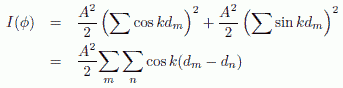　　(6.2)

回折光強度は、それぞれの回折格子線の光路差の余弦を取ったものの和で評価されるます。 ここで一端、ある２本の格子線に注目してそれがどのような干渉を引き起こすかを見てみます。

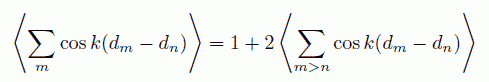　　(6.3)

光路差は m 番目の格子線との間の距離を x_m とすれば、 x_m sin ϕ ですから、 その平均は m 番目の格子線の分布関数を用いて次式で表されます：

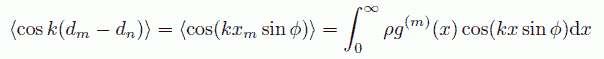　　(6.4)

ここで y = k l_v sin ϕ、α = a/l_v と置き、オイラーの関係式を使って簡単化すると、 第 m 近接分子との間の分布関数のフーリエ変換の形になり、次の関係式が得られます

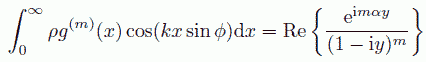　　(6.5)

回折線の強度はこれをすべての近接分子対について足しこめばよく、 等比級数の和の形になるので容易に下式のような表現を得ることができます。

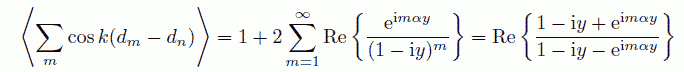　　(6.6)

あからさまな形で書けば、回折強度は次のように与えられます。

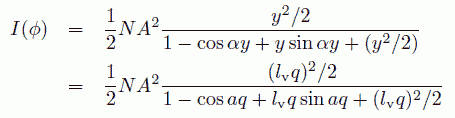　　(6.7)

ここで今日的な表記とあわすために下式で定義される q を使った表記も合わせて示しました。 構造因子といわれるものは、この回折強度の式で等方的な散乱 NA²/2 の寄与を除いたものです （実際には原子内の干渉の効果があって単純ではなく、原子散乱因子を考慮する必要があるのですが）

　　(6.8)

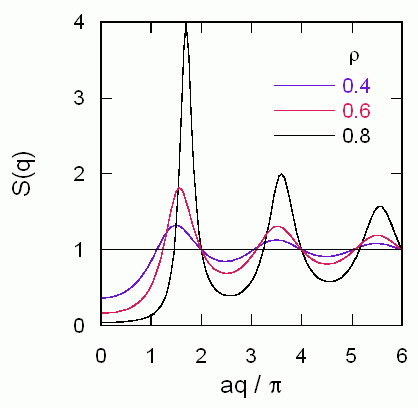
図には計算される構造因子 S(q) = 2 I(q)/(NA²) のグラフを示しました。 密度が高くなるにつれ、明瞭な振動構造が現れてきます （剛体棒流体では aq = 2nπ (n > 0) で構造因子が 1 になります）。

なお特に小角での回折強度については、次のような表式が与えられます。 これは粒子数の揺らぎと関わる量で、すでに光散乱と関わって Ornstein-Zernike の論文中で議論されたところです。

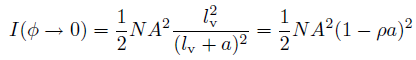　　(6.9)

この式から出発して状態方程式を得ることは容易なのですが（付録の(a.4)式にあるように、粒子数揺らぎと関係付けることで、 ∂ρ/∂P = β(1 - ρa)² という式を得、これを積分し、 ρ→0 で理想気体の状態方程式 βP = ρ になることを用いれば、 Korteweg-Tonks の式（(7.7) 式）が得られる）、 なぜか Zernike-Prins は導出を行っていません。 彼らの主たる問題関心がＸ線の回折であったためなのでしょうが・・・