７．１次元流体の熱統計力学

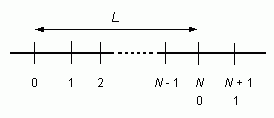
ここまで Zernicke と Prins の論文で展開された１次元剛体棒流体の構造についての議論を紹介しました。 違和感を持たれた方があるかもしれませんが、１次元剛体棒流体の構造に関して、 温度や圧力はあからさまな形ではまったく登場しません。 ここでは比較的標準的な手法による、１次元流体の統計力学的取り扱いについて紹介します。

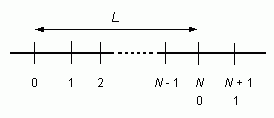
取扱いを簡単にするために、周期境界条件で考えます。 図のようにある分子（0 番目の分子とします）の位置を原点に固定し、 N 個目からもう一度同じ配置を繰り返すとします。 周の長さ L の円い輪の上に N 個の分子を順番に座標の正の方向に配置したと思っていただいてもよいでしょう。 また便宜上、N 番目の分子（N + 1 個目の分子）は 0 番目の分子が繰り返し登場してきたとみなし、 その座標の値がちがう（x_N = L）ものとして扱います。

この系のカノニカルの配置の状態和（分配関数）は次のように表されます。

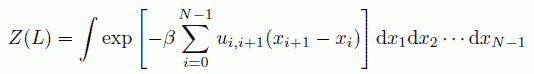　　(7.1)

ここでβは温度の逆数、u(r) は分子間の対ポテンシャルエネルギーを表します。 積分は原点に固定した分子を除く N - 1 個の分子の座標について行います。 この積分が畳み込み積分の形になっていることに注目します。 畳み込み積分ですから、L に関するラプラス変換（あるいはフーリエ変換）を施してやれば、 これは簡単な形に整理できます。 このラプラス変換と同等の操作は、NLT 一定の条件の系（カノニカル集団）の状態和から、 NPT 一定の状態和 Y(P) に移行することで行うことができます。

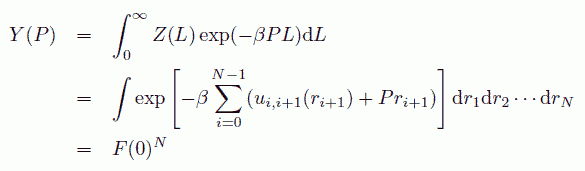　　(7.2)

ここで登場する関数 F(s) は下式で定義されます。

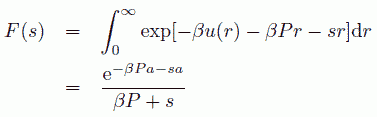　　(7.3)

さて NPT 一定での状態和は、化学ポテンシャルと次の関係で結ばれます （系が加成的なので化学ポテンシャルの N 倍がギブズの自由エネルギーになる）。

　　(7.4)

　　(7.5)

ここで λ_th は熱的ドブロイ波長で、 １次元の理想気体であれば化学ポテンシャルは T ln (ρλ_th) になります。 状態方程式は化学ポテンシャルの圧力微分から得られ、 剛体棒流体であれば Korteweg-Tonks の式が導かれます。

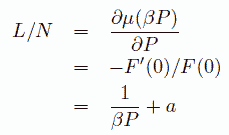　　(7.6)

Korteweg-Tonks の式は、次の形でも書けます （この形の方がビリアル方程式との対応がよい）。

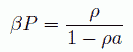　　(7.7)

動径分布関数について言うと、 デルタ関数を使って書くのが便利です。 原点から x の場所の密度は動径分布関数で ρg(r) と書け、これはデルタ関数を使って次式で評価できます。

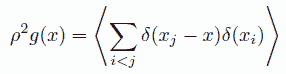　　(7.8)

この計算での問題は、すでに Zernike-Prins の扱いでも出てきましたが、 距離 r までに何個の分子が入っているかです。 ここで再びラプラス変換の登場です。 ラプラス変換を使うと、次のように見通しよく計算が行えます。

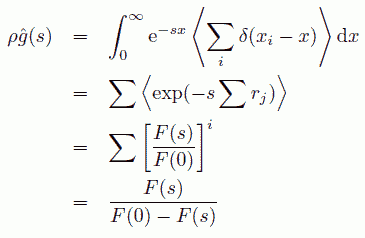　　(7.9)

ここで s を i q とおき実数部を取り出せば、 先の Zernike-Prins の導いた構造因子が導出できます。

さてこの章の最後に Ornstein-Zernike の式について触れておきましょう。 １次元剛体棒流体の動径分布関数の式を、畳み込み積分を使って下記のような式に整理することができます。

ρg(x) = ρg⁽¹⁾(x) + ρg⁽¹⁾(x)*ρg⁽¹⁾(x) + ρg⁽¹⁾(x)*ρg⁽¹⁾(x)*ρg⁽¹⁾(x) + ・・・
= ρg⁽¹⁾(x) + ρg⁽¹⁾(x) * ρg(x)　　(7.10)

Ornstein-Zernike の式は、直接相関関数と呼ばれる関数 c(x) を導入し、 全相関関数 h(x) = g(x) - 1 を次のように表現しようとするものです。

ρh(x) = ρc(x) + ρc(x)*ρc(x) + ρc(x)*ρc(x)*ρc(x) + ・・・
= ρc(x) + ρc(x) * ρh(x)　　(7.11)

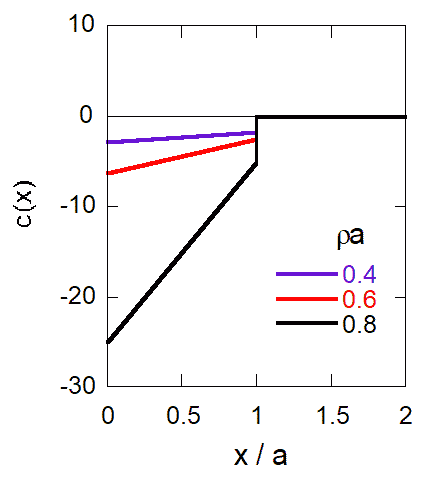図．　１次元剛体棒流体の直接相関関数 c(x)。 c(x) は x < a でしか値を持たず、x = a で不連続。

１次元の剛体棒流体の動径分布関数の表現と、 このOrnstein-Zernike の式は非常によく似た構造を持っています。 剛体棒流体の場合、直接相関関数は次のように与えられます。

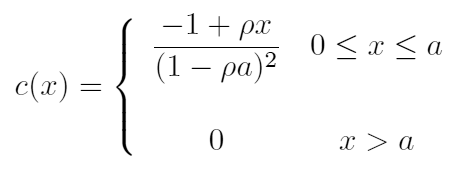　　(7.12)

直接相関関数は剛体棒のコアの内部（|x| < a）でしか値を持たず、 x = a で不連続性を示します （直接相関関数の x = a での不連続性が、ちょうど全相関関数の不連続性を打ち消し、 h(x) - c(x) は連続関数になります）。 直接相関関数の挙動と、最近接対間の分布関数との関わりは興味深いのですが、 今のところぼくにはその関わりを見渡すだけの力がありません。

久しぶりに見直してみて、直接相関関数の式(7.12)・図にとんでもない間違いがあったので訂正しました。 急いで作ったページとはいえ、何ともお恥ずかしい次第です。
20017.8.26.