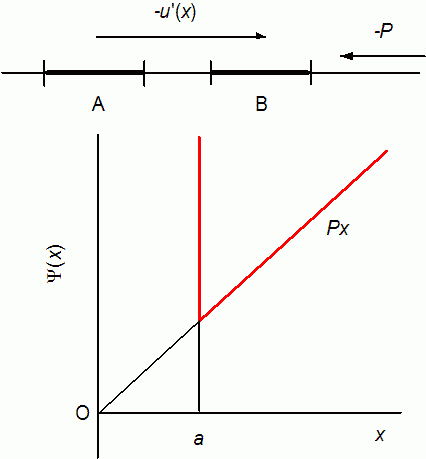
図. 1次元流体中の分子に働く有効ポテンシャル。 分子Bは分子Aの近傍で有効ポテンシャル ψ(x) = u(x) + Px の下で運動する。
先の章で(ぼくの感じる意味で)正統的な統計熱力学的なアプローチを紹介しました。 ここではもっと砕けた形で、1次元の流体のお話をしましょう。

1列に並んだ分子のある近接した分子対 AB を取り出したとしましょう。 この AB 対の間の距離 r を固定して、A の近傍で B に働く力を考えます。 まず A からは分子間力 -u'(r) が働いています。 そして逆サイドからは、他の分子が近づいたり遠ざかったりしながら B に力を及ぼします。 この他の分子から及ばされる力は、平均的に考えると系の圧力 -P になるはずです。 つまり平均的に見れば、A から r 離れたところにある分子 B は、図に見るような有効ポテンシャル
ψ(x) = u(x) + Px (8.1)
を感じながら運動しているわけです。
ですから近接分子間の分布関数 g(1)(r)は、前章と同じく次の式で与えられます。
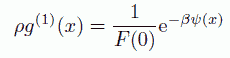 (8.2)
(8.2)
ここで F(0) は規格化のための定数ということになります。 第2近接分子間、第3近接分子間の動径分布関数は、 Zernike-Prins の扱いと同様、近接分子間の分布関数の畳み込み積分で評価できます。 また状態方程式は、近接分子間の平均距離が、分子1個あたりの長さになることから、 次の式で与えられます。
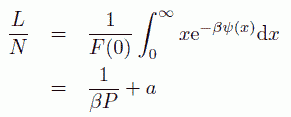 (8.3)
(8.3)
先の状態和から出発するアプローチでは、 NPT アンサンブルへの拡張は、畳み込み積分を計算するための計算手法という色合いが濃厚でした。 ここではそれが1分子に働く有効ポテンシャルという形で立ち現われてきます。 そして何より「圧力」というものが、分子に加わるポテンシャルに直接的に登場することは興味深いことです。 1次元の液体では圧力は分子同士をつなぎ止める引力として立ち現われ、 そして圧力が負になることは、直ちに系の不安定性に直結します(F(0) の値が発散)。 また「圧力一定」という条件は分子にとって、いわば“自然な条件”として現われます。
このような圧力の位置づけは、2次元、3次元の液体ではもはや成り立ちません。 2次元、3次元の液体では、液体の表面にかかる圧力が、 そのままでは分子の表面に働く応力には等しくなりません。 ですから「圧力一定」という条件は、2次元、3次元の液体中の分子の特性を考える上では、 厄介な拘束条件となります。 またあるいは2次元、3次元の液体で圧力が負になることは、直ちに系の不安定性に直結しません(準安定状態)。 このことが2次元、3次元の液体において、気液の相転移をもたらすと考えることもできるでしょう。