
セミナーではもう少し手の込んだ会合モデルを取り上げたのですが、 ここでは単純化した話にしてみました。 平衡定数が、位相空間での(重みをもった)体積比になっていることを感じ取ってもらえればよいのですが・・・

|
| 図 3a. モデル会合平衡。 A の周り半径 \(r\) の球内にある B は、会合体 AB を作っていると考えます。 |
化学反応にともなうエネルギー、エンタルピーの変化を考えるために、 分子種 A と B が溶媒 S 中で会合体 AB を形成するとても仮想的な化学平衡を考えます。 溶液の体積は \(V\) で一定で、A と B は無限希釈量存在するものとします。 そして A B 間の距離が \(r\) 以内にある AB のペアを、会合体 AB であるものと見なし、 A B 間には相互作用がなく独立に振舞うものとします。
さて A、B の濃度は十分低いので、A の周り半径 \(r\) の球同士の重なりや、 B が球内に 2 個以上存在するような場合は無視できます。 会合体 AB の数 \(N_\mrm{AB}\) は、A(あるいは B)の周り \(r\) 以内の空間に存在する B(あるいは A)の数ですから、 下式のように評価できます:
\begin{equation} \langle N_\mrm{AB} \rangle = \frac{4}{3} \pi r^3 N_\mrm{A} C_\mrm{B} \label{eq:numab} \end{equation}
ここで \(\langle N_\mrm{AB} \rangle\) は AB の数の期待値(平衡値)を示します。 会合体 AB の平衡濃度 \({}^{\natural} C_\mrm{AB}\) は \(\langle N_\mrm{AB} \rangle /V\)ですから、 会合平衡 A + B ⇌ AB の熱力学平衡定数は次式で与えられます:
\begin{equation} K = \frac{C^\circ {}^{\natural} C_\mrm{AB}}{C_\mrm{A} C_\mrm{B}} = \frac{4}{3} \pi r^3 C^\circ = v_\mrm{AB} C^\circ \label{eq:econab} \end{equation}
ここで \(C^\circ\) は標準状態の数密度で、 簡単のため会合体と認定する領域の体積を \(v_\mrm{AB}\) とおきました:
\begin{equation} v_\mrm{AB} = \frac{4 \pi}{3} r^3 \end{equation}
式 \eqref{eq:econab} の平衡定数からエンタルピー変化を求めてみましょう。 平衡定数が温度依存性を持たないので、先のファントホッフの式から次のようになります:
\begin{equation} \Delta_\mrm{r}H^\circ = - k_\mrm{B} \pdifA{\ln K}{(1/T)}{P, N_k} - \alpha k_\mrm{B} T^2 = - \alpha k_\mrm{B} T^2 \label{eq:entch0} \end{equation}
ここで気体定数ではなく、ボルツマン定数 \(k_\mrm{B}\) を用いているのは、 物質量の単位をモルではなく個数に取っていることによります( \(R = N_\mrm{A} k_\mrm{B}\))。 溶媒 S の膨張率が正なら、この会合平衡は発熱反応ですし、4 °C 以下の水のように膨張率が負なら吸熱反応というわけです。
この結果にちょっと意外な感を持つ人がいるかもしれませんが、 気相反応の場合を想像してみてください。 A + B → AB という反応が起きれば、分子数が半分になるので、エンタルピーは内部エネルギーの変化がなくとも、 \(P \Delta_\mrm{r} V = -RT\) だけ変化します。 理想気体の膨張率は \(1/T\) ですから、式 \eqref{eq:entch0} の結果と一致することが分かります。
ここで考えた会合反応は、ただたまたま A の近くを B が通りかかっただけのことで、 「反応」というのもはばかられるものと言えるでしょう。 けれどもエンタルピー変化は起きるのです。 この事情を (1) 体積一定の条件での圧力低下、(2) 圧力変化の補償の2段階に分けて考えてみましょう。
この反応では B(あるいは A)が、ある領域に閉じ込められてしまうことに注意しましょう。 つまり B は自由に体積 \(V\) の空間の中を動き回ることができなくなるわけです。 このことは半透膜で B を溶液から隔離したことに相当します。 半透膜で溶液から隔離する、このことで浸透圧が発生することに注意してください。 系の体積を一定に保っていると、 B が隔離される結果、圧力が(浸透圧の)ファントホッフの式に従って \(k_\mrm{B}T/V\) だけ低下します。
\begin{equation} (\Delta_\mrm{r} P)_V = \pdifA{P}{\xi}{V} = -\frac{k_\mrm{B} T}{V} \label{eq:pchange} \end{equation}
この圧力の低下の結果、エンタルピーは \(k_\mrm{B} T\) だけ減少します(\(H = U + PV\))。
\begin{equation} \Delta_{1} H = -\frac{k_\mrm{B} T}{V} V = -k_\mrm{B} T \label{eq:hchange1} \end{equation}
ことはこれだけに止まりません。 温度・圧力一定の条件でエンタルピー変化を観測するので、\(k_\mrm{B}T/V\) 低下した圧力を元の圧力に戻さなければなりません。 このことにともなうエンタルピー変化が生まれます。
\begin{eqnarray} \Delta_{2} H &=& \pdifA{H}{P}{T,N_k} \frac{k_\mrm{B} T}{V} \\ &=& \left[\pdifA{H}{P}{S, N_k} + \pdifA{H}{S}{P, N_k} \pdifA{S}{P}{T, N_k} \right] \frac{k_\mrm{B} T}{V} = \left[ V - T \pdifA{V}{T}{P, N_k} \right] \frac{k_\mrm{B} T}{V} \\ &=& k_\mrm{B} T - \alpha k_\mrm{B} T^2 \label{eq:hchange2} \end{eqnarray}
最終的に観測されるエンタルピー変化は次のようになり、 先の(平衡定数の温度依存性に対する)ファントホッフの式の結果(式 \eqref{eq:entch0})が得られることが分かります:
\begin{equation} \Delta_\mrm{r} H = \Delta_{1} H + \Delta_{2} H = - \alpha k_\mrm{B} T^2 \label{eq:hchange} \end{equation}
ここではエンタルピー変化に注目しましたが、 同様のことは体積変化に関しても見られます。 エンタルピー変化の場合には、一端減少したエンタルピー変化 \(k_\mrm{B}T\)(式 \eqref{eq:hchange1})を、 圧力を元に戻す際に補償する(式 \eqref{eq:hchange2} 第1項)という、少し複雑なやり取りでしたが、 体積変化は、圧力を元に戻す(圧縮して圧力を \(k_\mrm{B}T\) だけ増加させる)過程だけ考えればよいので、もっと単純です:
\begin{eqnarray} \Delta_\mrm{r} V &=& \pdifA{V}{P}{T,\xi} \frac{k_\mrm{B} T}{V} \\ &=& -\kappa_T k_\mrm{B} T \label{eq:vchange} \end{eqnarray}
ここでは \(\kappa_T\) は溶媒の等温圧縮率です(\(\kappa_T = -(1/V) (\partial V/\partial P)_T\) )。 理想気体を考えていただくと等温圧縮率は \(1/P\) で、A + B → AB の反応の体積変化が 1 mol あたり \(-RT/P\) になり、 「気体反応の法則」に相当していることがお分かりでしょう。
ここまでの話を図式化してみると、体積一定で考えた時に現れる反応の圧力変化は溶媒の種類によらず \(-k_\mrm{B} T/V\) で同じなのですが、 圧力一定という条件で考える時には、溶媒というフィルターを通して、 エンタルピーや体積の変化として現れていることになります。 そしてそのフィルターには、液体の膨張率や圧縮率という、分子論的には一筋縄でいかない要素が関わっているわけです。

|
図 3b. ここで見ているエンタルピー、体積変化は、 体積一定の条件で現れる圧力の変動 \(k_\mrm{B} T/V\) に対する、 圧力一定の条件での溶媒の応答であると見ることができます。 |
エンタルピー変化の生まれる事情を事細かく見たわけですが、 皆さんが学んだであろう分配関数(状態和)を用いた取り扱いとの対応を見ておきましょう。
A、B は内部構造のない単原子分子だとします。 半古典的には単原子分子 X の化学ポテンシャルは次式で与えられます:
\begin{equation} \mu_\mrm{X} = k_\mrm{B} T \ln (\lambda_\mrm{X}^3 C_\mrm{X}) + w_\mrm{X} \label{eq:cpx} \end{equation}
ここで右辺第1項は理想気体状態の化学ポテンシャル、\(w_\mrm{X}\) は溶媒への溶解の際の自由エネルギー変化です。 そして \(\lambda_\mrm{X}\) は分子 X の熱的(ドブロイ)波長と呼ばれるものです:
\begin{equation} \lambda_\mrm{X} = \sqrt{\frac{h^2}{2\pi m_\mrm{X} k_\mrm{B} T}} \label{eq:thwavelength} \end{equation}
ここで \(h\) はプランク定数、\(m_\mrm{X}\) は X の質量で、 半古典的な扱いでは \(\lambda_\mrm{X}\) が分子の大きさなどに比べて十分小さいと考えます。 さて ”会合体” AB の化学ポテンシャルですが、こちらは内部構造を持っているので、 内部構造に起因する分配関数 \(z^\mrm{int}_\mrm{AB}\) の項を加えておく必要があります。
\begin{equation} \mu_\mrm{AB} = -k_\mrm{B} T \ln z^\mrm{int}_\mrm{AB} + k_\mrm{B} T \ln (\lambda_\mrm{AB}^3 C_\mrm{AB}) + w_\mrm{AB} \label{eq:cpab} \end{equation}
内部構造と言っても、AB 間の相互作用や、溶媒分子を介しての間接の相互作用など無視しているので、 距離 \(R\) 以内を保ちながら運動する2原子系を考えればよく、 \(z^\mrm{int}_\mrm{AB}\) は AB の換算(実効)質量 \(m_\mrm{r} = m_\mrm{A} m_\mrm{B}/(m_\mrm{A} + m_\mrm{B})\) を用いて次式のようになります。
\begin{equation} z^\mrm{int}_\mrm{AB} = \left[ \frac{h^2}{2\pi m_\mrm{r} k_\mrm{B} T} \right]^{-3/2} v_\mrm{AB} \label{eq:zintab} \end{equation}
A と B は独立に振舞っていると考えているので、 溶解の際の自由エネルギー変化について \(w_\mrm{AB} = w_\mrm{A} + w_\mrm{B}\) です。 そうすると会合平衡 A + B ⇌ AB のギブズエネルギー変化は次式で与えられます:
\begin{eqnarray} \Delta_{\mrm{r}}G &=& \mu_\mrm{AB} - (\mu_\mrm{A} + \mu_\mrm{B}) \\ &=& -k_\mrm{B} T \ln v_\mrm{AB} + k_\mrm{B} T \ln \frac{C_\mrm{AB}}{C_\mrm{A} C_\mrm{B}} \\ &=& -k_\mrm{B} T \ln (v_\mrm{AB} C^\circ ) + k_\mrm{B} T \ln \frac{C^\circ C_\mrm{AB}}{C_\mrm{A} C_\mrm{B}} \label{eq:dg} \end{eqnarray}
この「会合反応」で、 最初 A と B が持っていた並進運動エネルギー \(3k_\mrm{B}T\) (\(= 2 \x (3/2) k_\mrm{B}T\))が、 AB 分子の内部エネルギー \((3/2)k_\mrm{B}T\) と 並進運動エネルギー \((3/2)k_\mrm{B}T\) に転換されています。 たぶん皆さんが教科書で勉強した反応例では、分子の内部エネルギーとしては、AB の結合エネルギーを除くと、 AB 分子の回転エネルギー \(k_\mrm{B}T\) と量子化された調和振動のエネルギーだというシナリオだったでしょう。 そして AB の振動のエネルギーには、古典的にはエネルギー等分配則で 2 自由度割り当てられ \(k_\mrm{B}T\) のエネルギーを持つことになっていたと思います 【2原子分子気体の定容モル熱容量 \(C_{\mrm{m},V}\) は常温では \((5/2)R\) (比熱比 1.40)、温度を上げ振動の寄与が増してくると \((7/2)R\) (比熱比 1.29)に漸近する(試験に出る!?)】。 ここでは古典的に扱っているので、内部エネルギーが \(2 k_\mrm{B}T\) になりそうですが、 \((3/2) k_\mrm{B}T\) に止まります。 これはここで扱っている振動に対応する運動が、AB 間距離を \(r\) 以内に限定しただけの運動なので、 教科書で扱う調和振動とは話が違ってくるためです(調和振動でバネ定数を小さくすると、振幅はいくらでも大きくなります)。
こうして少し回り道でしたが、分配関数を考える立場からでも、 先の初等的な手続きによる平衡定数についての表式(式 \eqref{eq:econab})が得られます:
\begin{equation} K = \frac{C^\circ {}^{\natural}C_\mrm{AB}}{C_\mrm{A} C_\mrm{B}} = v_\mrm{AB} C^\circ \label{eq:smk} \end{equation}
|
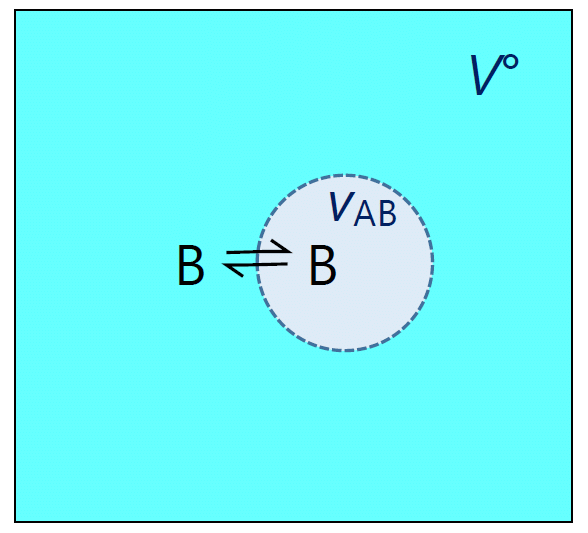
| 図 3c. 会合体 AB の生成平衡は、体積 \(V^\circ\) の領域と体積 \(v_\mrm{AB}\) の領域の間の分配平衡と見なせます。 |
えられた平衡定数の表現を見てみると、 これは体積 \(V^\circ\)(\(= 1/C^\circ\))の中で運動している B(あるいは A)分子が、 体積 \(v_\mrm{AB}\) の領域の中に存在する確率、 あるいは2つの領域の間の分配平衡に相当していることが分かります(\(V^\circ \gg v_\mrm{AB}\) )。
\begin{equation} K = v_\mrm{AB} C^\circ = \frac{v_\mrm{AB}}{V^\circ} \label{eq:smkx} \end{equation}
それぞれの領域に存在する確率はその体積に比例していると考えているわけですが、 これは分配定数 \(K_\mrm{D} = 1\) の ”分配平衡” を考えていることになります。 実際、さきに分配関数からの平衡定数の導出を見ましたが、 ある分子種の分配関数というのはいわば位相空間の中で占める体積に相当していて、 平衡定数は AB 会合体が運動する体積 \(v_\mrm{AB} \x V^\circ\) と、A と B が独立に運動する体積 \(V^\circ \x V^\circ\) の比になっていました。
もっと言えば、この「体積」というのは、カノニカルな系ではボルツマン因子 \(\exp(-u/k_\mrm{B}T)\) の重み(測度)を持つ体積で、 ”分配定数” \(K_\mrm{D}\) はボルツマン因子ということになります。
平衡定数がこうした ”分配平衡” に対応している考えれば、 その ”分配定数” が \(K_\mrm{D} = 1\) で一定であることから、 エンタルピー変化は先に見た通り次式のようになります:
\begin{eqnarray} \Delta_\mrm{t}H &=& - R \pdifA{\ln K_\mrm{D}}{(1/T)}{P, N_i} + [\alpha(\mrm{Y}) - \alpha(\mrm{X})] RT^2 \\ &=& - \alpha RT^2 \label{eq:hchangetr} \end{eqnarray}
ここで X 相は溶液中で分子が動き回っている領域、Y 相は会合分子 AB の占める領域で、 会合分子 AB の占める領域の体積 \(v_\mrm{AB}\) の膨張は起きないので \(\alpha(\mrm{Y}) = 0\) としています。 この式 \eqref{eq:hchangetr} は、先の式 \eqref{eq:entch0}、式 \eqref{eq:hchange} とも合致していて、 平衡定数に対する”分配平衡描像” の妥当性が確認できます。
この章のおしまいに、質量モル濃度、組成にもとづく標準状態を取る場合にどのような風景が見えるかに触れておきましょう。 先の平衡定数式 \eqref{eq:econab}を、質量モル濃度にもとづく熱力学平衡定数 \(K(m~\mrm{basis})\) で表現すれば、次のようになります:
\begin{equation} K(m~\mrm{basis}) = \rho_\mrm{S} m^\circ v_\mrm{AB} \label{eq:econmx} \end{equation}
ここで \(m^\circ\) は標準質量モル濃度で、 \(\rho_\mrm{S}\) は溶媒の質量密度です。 質量モル濃度にもとづく熱力学平衡定数は溶媒の密度の関数になり、 温度依存性を持つようになります。 そして反応にともなうエンタルピー変化としてファントホッフの式から、 先の濃度にもとづく標準状態を取った場合の式 \eqref{eq:entch0} と同じ結果を与えます:
\begin{equation} \Delta_\mrm{r}H^\circ = - k_\mrm{B} \pdifA{\ln K(m~\mrm{basis})}{(1/T)}{P, N_k} = - k_\mrm{B} \pdifA{\ln \rho_\mrm{S}}{(1/T)}{P, N_k} = - \alpha k_\mrm{B} T^2 \label{eq:entchm} \end{equation}
質量モル濃度にもとづく平衡定数では、 熱力学平衡定数の表現の中に溶媒の質量密度が組み込まれることになります。 先の平衡定数に対する”分配平衡描像”(式 \eqref{eq:smkx})で言えば、設定した標準濃度で決まる体積 \(V^\circ\)(\(= 1/C^\circ\)) の代わりに溶媒の比容 \(1~\mrm{kg}/\rho_\mrm{S}\) を持ち出したことになっているわけです (わかりやすいように \(m^\circ = 1~\mrm{kg}^{-1}\) としておきます)。 A と B の会合の判断に、第3者である(と思われる)溶媒 S の比容が持ち出されることに、 ぼくなどは違和感を持ちますが、皆さんはいかがでしょう?