さて問題の平衡定数の温度依存性の問題に入るわけですが、 熱力学の関係式を整理しておきましょう。 まずギブズエネルギー \(G\) は、ギブズ-ヘルムホルツの式(プランク関数の式とも)から エンタルピー \(H\) と次の関係で結ばれます:
\begin{equation} \pdifA{(G/T)}{(1/T)}{P, n_k} = H ~~\mbox{あるいは}~~ \pdifA{(G/T)}{T}{P,n_k} = -\frac{H}{T^2} \label{eq:ghrel} \end{equation}
同様に微分の順序交換から、部分モル量に関しても同様の関係が成り立ちます:
\begin{equation} \pdifA{(\mu_i/T)}{(1/T)}{P, n_k} = H_i ~~\mbox{あるいは}~~ \pdifA{(\mu_i/T)}{T}{P, n_k} = -\frac{H_i}{T^2} \label{eq:ghrelpq} \end{equation}
反応のギブズエネルギー変化の温度微分も同様にして
\begin{equation} \pdifA{(\Delta_\mrm{r} G/T)}{(1/T)}{P, n_k} = \Delta_\mrm{r}H~~\mbox{あるいは}~~ \pdifA{(\Delta_\mrm{r} G/T)}{T}{P, n_k} = -\frac{\Delta_\mrm{r}H}{T^2} \label{eq:rgct} \end{equation}
のように、反応のエンタルピー変化 \(\Delta_\mrm{r}H\) と関係づけられます。 ですから熱力学平衡定数と標準状態の反応のギブズエネルギーの関係 \(\Delta_{\mrm{r}}G^\circ = -RT \ln K\) から、次のような関係が成り立ちます:
ちょっと待て!! \begin{equation} \pdifA{\ln K}{(1/T)}{P, n_k} = -\frac{\Delta_\mrm{r}H^\circ}{R}~~\mbox{あるいは}~~ \pdifA{\ln K}{T}{P, n_k} = \frac{\Delta_\mrm{r}H^\circ}{R T^2} \label{eq:vanthoff0} \end{equation} ちょっと待て!!
これで何の問題もないように見えますが、ここには落とし穴があるのです。
そもそもの、反応のギブズエネルギー変化の式 に立ち戻ってみましょう。
\begin{equation} \Delta_{\mrm{r}}G = \Delta_{\mrm{r}}G^\circ + RT \ln \prod_i {c_i^{\nu_i}} - RT \ln {c^\circ}^{\sum_i {\nu_i}} \label{eq:gchange0} \end{equation}
ギブズ-ヘルムホルツの式から、この両辺を温度 \(T\) で割り、 圧力 \(P\)、各物質量 \(n_k\) 一定の条件で \(1/T\) で微分すれば、反応のエンタルピー変化が得られます:
\begin{eqnarray} \Delta_{\mrm{r}}H &=& \pdifA{(\Delta_{\mrm{r}}G/T)}{(1/T)}{P, n_k} \\ &=& \pdifA{(\Delta_{\mrm{r}}G^\circ /T)}{(1/T)}{P, n_k} + R \pdifA{\ln \prod_i {c_i^{\nu_i}}}{(1/T)}{P, n_k} \label{eq:hchangex} \end{eqnarray}
標準状態の濃度 \(c^\circ\)(1 mol/L)は一定なので、式 \eqref{eq:gchange0} の右辺第3項は寄与しません。 しかし第2項、反応・生成物の濃度 \(c_i\)(\(= n_i /V\))は熱膨張によって変化するので、 溶液の膨張率を考慮しないといけません。 少していねいに(くどく)関係を追っておくと、次のようになります:
\begin{equation} \pdifA{\ln c_i}{(1/T)}{P, n_k} = -\pdifA{\ln V}{(1/T)}{P, n_\mrm{S}} = \frac{T^2}{V}\pdifA{V}{T}{P, n_\mrm{S}} = \alpha T^2 \label{eq:expansibility} \end{equation}
|
| 図 2a. 溶媒 S 中に無限希釈量溶けた A と B が会合して AB となる |
ここで \(\alpha\) は溶媒の膨張率( \(\alpha = (1/V)(\partial V/\partial T)_{P, n_\mrm{S}}\) )で、 反応・生成物が無限希釈の状態を考えているので、溶液の膨張率は溶媒の膨張率と等しくなります。 そして 式 \eqref{eq:hchangex} に \(\Delta_{\mrm{r}}G^\circ = -RT \ln K\) の関係を用いると、 A と B の会合平衡 A + B ⇌ AB の場合、次の式を得ます:
\begin{equation} \pdifA{\ln K}{(1/T)}{P, n_k} = -\frac{\Delta_\mrm{r}H^\circ}{R} + {\sum_i {\nu_i}} \alpha T^2 = -\frac{\Delta_\mrm{r}H^\circ}{R} - \alpha T^2 \label{eq:vanthoffxx} \end{equation}
このように、先の式 \eqref{eq:vanthoff0} では見過ごされていた、 溶液の膨張に由来する寄与が現れます。 この項(\(\alpha T^2\))は反応にともなう量だから現れるというわけではありません。 溶質の化学ポテンシャルは、標準状態での化学ポテンシャル \(\mu^{\circ}_i\) を用いて次のように表されます:
\begin{equation} \mu_i = \mu^{\circ}_i + RT \ln c_i/c^{\circ} \label{eq:cp0} \end{equation}
この式から部分モルエンタルピー \(H_i\) をギブズ-ヘルムホルツの式から求めてみましょう。 標準状態の濃度 \(c^{\circ}\) は、 温度、圧力依存性を持たないので、次の関係式が得られます。
\begin{eqnarray} H_i &=& \pdifA{(\mu_i/T)}{(1/T)}{P, n_k} = \pdifA{(\mu^{\circ}_i/T)}{(1/T)}{P, n_k} + RT \pdifA{\ln c_i}{(1/T)}{P, n_k} \label{eq:cp1a} \\ &=& \pdifA{(\mu^{\circ}_i/T)}{(1/T)}{P, n_k} + \alpha RT^2 \label{eq:cp1b} \end{eqnarray}
溶質の化学ポテンシャルの温度依存性から、溶質の標準部分モルエンタルピー \(H^\circ_i\) を導出する際にも、 やはり \(\alpha RT^2\) という項が現れます。 式 \eqref{eq:cp1a} の導出に、何かだまされたような印象を持つ人がいるかもしれませんが、 式 \eqref{eq:cp0} によらず、少していねいに(くどく)式で書けば次のようになります (偏微分の際の条件をはっきり示すために、ここまで下付きで表示していたのを \(\{\cdots \}\) で表示するようにしました):
\begin{eqnarray} \pdif{(\mu_i/T)}{(1/T)} \{P, n_k\} &=& \pdif{(\mu_i/T)}{(1/T)} \{P, c_i, n_{k \ne i}\} + \pdif{(\mu_i/T)}{c_i} \{P, T, n_{k \ne i}\} \pdif{c_i}{(1/T)} \{P, n_k\} \label{eq:cpx1} \\ &=& \pdif{(\mu_i/T)}{(1/T)} \{P, c_i, n_{k \ne i}\} + \alpha RT^2 \label{eq:cpx2} \end{eqnarray}
式 \eqref{eq:cp1a} の右辺第1項は、 次式に相当しているわけです。
\begin{equation} \pdifA{(\mu^{\circ}_i/T)}{(1/T)}{P, n_k} = \pdif{(\mu_i/T)}{(1/T)} \{P, c_i, n_{k \ne i}\} \label{eq:cp1ax} \end{equation}
十分低い濃度では(無限希釈状態)では、この値は成分 \(i\) の濃度に依存しません (標準状態に取っているのは仮想的な \(c_i = c^\circ\) の状態であることに注意)。 また式 \eqref{eq:cpx1} の右辺第2項について、 無限希釈で成立する次式の関係を用いて、式 \eqref{eq:cpx2} を得ています (この積分形が式 \eqref{eq:cp0} であり、\(\mu_i^\circ\) は積分定数に相当しています)。
\begin{equation} \pdifA{\mu_i}{c_i}{P, T, n_{k \ne i}} = \frac{RT}{c_i} \label{eq:dilcp} \end{equation}
さて長々と熱力学平衡定数の温度依存性について述べてきたわけですが、 ここらでまとめておくと、ファントホッフの式は次のように表記されることになります:
濃度にもとづいて標準状態を取った場合のファントホッフの式 \begin{equation} \pdifA{\ln K}{(1/T)}{P, n_k} = -\frac{\Delta_\mrm{r}H^\circ}{R} + {\sum_i {\nu_i}} \alpha T^2~~\mbox{あるいは}~~ \pdifA{\ln K}{T}{P, n_k} = \frac{\Delta_\mrm{r}H^{\circ}}{RT^2} - {\sum_i {\nu_i}} \alpha \label{eq:vanthoff} \end{equation}
くどいようですが、A と B の会合平衡 A + B ⇌ AB の場合は次のようになります:
\begin{equation} \pdifA{\ln K}{(1/T)}{P, n_k} = -\frac{\Delta_\mrm{r}H^\circ}{R} - \alpha T^2~~\mbox{あるいは}~~ \pdifA{\ln K}{T}{P, n_k} = \frac{\Delta_\mrm{r}H^{\circ}}{RT^2} + \alpha \label{eq:vanthoffab} \end{equation}
さておはなしの最初の問題に立ち返ると、 膨張率の項を含まない教科書の式 \eqref{eq:vanthoff0}(表紙の式 (1))が成り立つためには、 式 \eqref{eq:hchangex} の第2項、濃度が温度依存性を持たなければよいことが分かります。 それには、組成比、質量モル濃度にもとづいて標準状態を取ればよいのです。 つまり溶媒の分子質量を \(M_\mrm{S}\) として、成分 \(i\) の質量モル濃度 \(m_i\)
\begin{equation} m_i = \frac{n_i}{M_\mrm{S} n_\mrm{S}} \label{eq:molality} \end{equation}
を用いて化学ポテンシャルを次式のように表すのです。
\begin{equation} \mu_{i} = \mu^{\circ}_i + RT \ln m_i/m^{\circ} \label{eq:cpm0} \end{equation}
こうすれば式 \eqref{eq:gchange0} 以下の式で \(c\) を \(m\) で置き換えればよいわけですから、
\begin{eqnarray} \Delta_{\mrm{r}}H = \pdifA{(\Delta_{\mrm{r}}G^\circ /T)}{(1/T)}{P, n_k} + R \pdifA{\ln \prod_i {m_i^{\nu_i}}}{(1/T)}{P, n_k} \label{eq:hchangemx} \end{eqnarray}
組成比、質量モル濃度は温度に依存しませんから、 式 \eqref{eq:hchangemx} の第2項は 0 で膨張率に依存する項は現れません。 同様にモル分率を採用した場合も、膨張率に依存する項は現れません(分圧表示の場合も同断です)。 これは先の部分モルエンタルピーの式 \eqref{eq:hchangex} についても同様です。
組成比、質量モル濃度にもとづいて標準状態を取った場合のファントホッフの式 \begin{equation} \pdifA{\ln K}{(1/T)}{P, n_k} = -\frac{\Delta_\mrm{r}H^\circ}{R}~~\mbox{あるいは}~~ \pdifA{\ln K}{T}{P, n_k} = \frac{\Delta_\mrm{r}H^{\circ}}{RT^2} \label{eq:vanthoffm} \end{equation}
なお濃度にもとづいて標準状態を取った場合でも、単に「1 mol/L」ではなく「25 °C で 1 mol/L」となるように、 温度に依存する標準状態を取れば、標準状態に組成比を取った場合の\eqref{eq:vanthoffm} と同じ表現となります。 具体的には、次のような表現を取ることになります:
温度に依存する濃度を標準状態に取った場合のファントホッフの式 \begin{equation} \pdifA{\ln K}{(1/T)}{P, N_k} = \pdifA{\ln (c^{\circ}(T)^{-{\sum_i {\nu_i}}} K_c)}{(1/T)}{P, N_k} = \pdifA{\ln K_c}{(1/T)}{P, N_k} - {\sum_i {\nu_i}} \alpha T^2 = -\frac{\Delta_\mrm{r}H^\circ}{R} \label{eq:vanthoffx} \end{equation}
実際の実験手順に即していえば、 温度依存性の実験をする際に、溶液の調製をすべて 25 °C で行い、 温度補正をしなければよいわけで手間が省けます。 これはある物質のトルエン溶液を 25 °C で 0.0500 mol/L で調製した時、 40 °C に昇温したら膨張して、濃度が 0.0492 mol/L 程度になるわけですが、 それを 0.0500 mol/L(← 0.0500 c°)であると見なすことに相当します。 考え方としては面白いのですが、こうした手法はデータの素性がよくわかっているうちは良いでしょうが、 データの数字だけが独り歩きするようになると、とんでもない混乱が起きかねず、 実際に採用する分にはお薦めしかねます。
おそらくこうした問題があるので、(ぼくは好みませんが)、 質量モル濃度にもとづく標準状態をとった 標準平衡定数 \(K^{\circ}\) を使用することが推奨されているのでしょう。 注意深く観察してもらうと、膨張率に依存する項の入っていないファントホッフの式 \eqref{eq:vanthoffm} が掲載されている教科書では、 式中、平衡定数の記号が標準平衡定数 \(K^{\circ}\) になっているのではないでしょうか。 残念ながら肝心の標準状態についての記載が省略されていることが多いようですが・・・
|
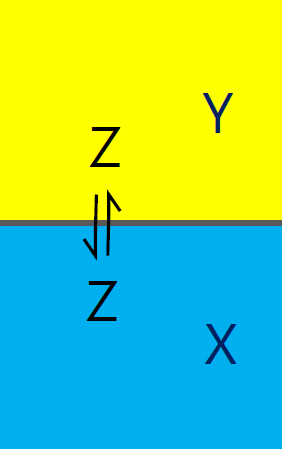
図 2b. 微量に溶け込んだ物質 Z の X 相と Y 相への分配平衡。 |
濃度を標準に取った場合と、組成比を標準に取った場合も、 反応の結果分子数の変化がなければ(量論係数の和が 0)、 熱力学平衡定数の値は同じで、 またファントホッフの式は同じ形になります。 けれども分子数の変化がなくとも、エンタルピー変化を考える上で、 膨張率の影響を考えないといけない場合があります。 そうした例として、水-トルエンの2液相間のエタノールの分配といった、 2液相間の分配平衡の問題を見てみましょう。
2種の互いに混じりあわない液体 X と Y が2相に分離しているとき、 ある物質 Z が X 相と Y 相に分配される比率、分配定数 \(K_\mrm{D}\) を考えます。 この分配定数は、もっぱら濃度を標準状態に取って記述されるので、 化学反応の平衡定数の場合同様、濃度にもとづく標準状態を取った議論をなぞりましょう。
以前はもっぱら分配係数 partition coefficient と呼ばれていましたが、 現在は分配定数 partition constant と呼ぶのが推奨されています。
2液相間で Z の分配平衡が成り立っているとき、X 相と Y 相中の Z の化学ポテンシャルは等しく、 次式が成り立ちます:
\begin{equation} \mu_\mrm{Z}(\mrm{X}) = \mu^{\circ}_\mrm{Z}(\mrm{X}) + RT \ln {}^{\natural}c_\mrm{Z}(\mrm{X}) /c^{\circ}(\mrm{X}) = \mu_\mrm{Z}(\mrm{Y}) = \mu^{\circ}_\mrm{Z}(\mrm{Y}) + RT \ln {}^{\natural}c_\mrm{Z}(\mrm{Y}) /c^{\circ}(\mrm{Y}) \label{eq:ptcon0} \end{equation}
この関係から、(熱力学)分配定数 \(K_\mrm{D}\) は次式で与えられます:
\begin{equation} RT \ln K_\mrm{D} = RT \ln \frac{{}^{\natural}c_\mrm{Z}(\mrm{Y})}{{}^{\natural}c_\mrm{Z}(\mrm{X})} + RT \ln \frac{c^{\circ}(\mrm{X})}{c^{\circ}(\mrm{Y})} = -[\mu^{\circ}_\mrm{Z}(\mrm{Y}) - \mu^{\circ}_\mrm{Z}(\mrm{X})] \label{eq:ptcon1} \end{equation}
通常、\(c^{\circ}(\mrm{X}) = c^{\circ}(\mrm{Y}) = 1 ~\mrm{mol/L}\) ととられ、 分配定数 \(K_\mrm{D}\) は次式のように書かれます:
\begin{equation} K_\mrm{D} = \frac{{}^{\natural}c_\mrm{Z}(\mrm{Y})}{{}^{\natural}c_\mrm{Z}(\mrm{X})} \label{eq:ptcon2} \end{equation}
さてこの分配定数 \(K_\mrm{D}\) の温度依存性から、 X 相から Y 相に移行する際のエンタルピー変化 \(\Delta_\mrm{t}H^{\circ}\) を評価するとどうなるでしょう? 先の化学反応のエンタルピー同様、次式が成り立ちます:
\begin{equation} \pdifA{\ln K_\mrm{D}}{(1/T)}{P, N_i} = -\frac{\Delta_\mrm{t}H^\circ}{R} + [\alpha(Y) - \alpha(X)] T^2~~\mbox{あるいは}~~ \pdifA{\ln K_\mrm{D}}{T}{P, N_i} = \frac{\Delta_\mrm{t}H^{\circ}}{RT^2} - [\alpha(Y) - \alpha(X)] \label{eq:transh} \end{equation}
質量モル濃度(組成比)にもとづく標準状態を取った場合には、 この X Y 両相の膨張率の差異に起因する項は現れません。
ここまでの議論を見ると、圧力一定で考えているので膨張率が関わってくることが分かります。 それでは体積一定の条件での平衡定数の温度依存性を考えてみたらどうでしょう? 温度・体積一定の場合にはヘルムホルツエネルギー \(F\) 変化が極小となる条件に注目することになります。 反応のヘルムホルツエネルギー変化についても、ギブズエネルギー変化の場合同様、次式が成立します (化学では出会う機会が余りありませんが、\((\partial F/\partial n_i)_{T,V,n_{k \ne i}} = \mu_i\) の関係に注意してください):
\begin{equation} (\Delta_{\mrm{r}}F)_{V} = \sum_i {\nu_i \mu_i} = \mu_\mrm{AB} - (\mu_\mrm{A} + \mu_\mrm{B}) \label{eq:hch0} \end{equation}
温度 \(T\)、体積 \(V\) 一定の条件の下での化学平衡状態では、 ヘルムホルツエネルギーが最小となり \(\Delta_{\mrm{r}}F = 0\) となるので、 次式が成り立ちます。
\begin{equation} (\Delta_{\mrm{r}}F^\circ)_{V} = -RT \ln {}^{\natural}Q = -RT \ln K \label{eq:eqconstv} \end{equation}
ギブズ-ヘルムホルツの式(マシュー関数の式)から式 \eqref{eq:ghrel} と同様に、 内部エネルギー \(U\) を与える次の関係が成り立ちます:
\begin{equation} \pdifA{(F/T)}{(1/T)}{V, n_k} = U \label{eq:ghreluv} \end{equation}
ですから、体積一定の条件での熱力学平衡定数の温度依存性から、 次式のように内部エネルギー変化を得ることができることになります(ファントホッフの等容線 van't Hoff's isochore):
濃度にもとづいた標準状態を取っても、組成比、質量モル濃度にもとづいた標準状態を取っても成立 \begin{equation} \pdifA{\ln K}{(1/T)}{V, n_k} = -\frac{(\Delta_\mrm{r}U^\circ)_V}{R}~~\mbox{あるいは}~~ \pdifA{\ln K}{T}{V, n_k} = \frac{(\Delta_\mrm{r}U^\circ)_V}{R T^2} \label{eq:vanthoffv} \end{equation}
なお体積一定の条件での内部エネルギー \(U\) の「部分モル内部エネルギー」 \(U_i\) は、 部分モルエンタルピーとは次の関係にあります(式 \eqref{eq:cp1b} 参照):
\begin{eqnarray} H_i &=& \pdifA{(\mu_i/T)}{(1/T)}{P, n_k}\\ &=& \pdifA{(\mu_i/T)}{(1/T)}{V, n_k} + \pdifA{(\mu_i/T)}{V}{T, n_k} \pdifA{V}{(1/T)}{P, n_k}\\ &=& U_i + \alpha R T^2 \label{eq:uandh} \end{eqnarray}
ここで成分 \(i\) が無限希釈状態にあるので、式 \eqref{eq:dilcp} 同様、 次の関係が成り立つことを用いています。
\begin{equation} \pdifA{\mu_i}{c_i}{T, V, n_{k \ne i}} = \frac{RT}{c_i} \label{eq:dilcpx} \end{equation}
外部との \(PV\) 仕事に由来するエネルギー変化が、 露わに見えているのが、この \(\alpha RT^2\) という項になっているわけです。 このあたりの事情を、もう少し詳しく、次の章で見てみることにします。
ここで「部分モル内部エネルギー」と呼んでいるものは、 正確には部分モル量ではなく、同次式に関するオイラーの関係式(ギブズ-デュエムの関係)を満たしません。 ただ適当な名称がないので、 このことに留意しつつ、部分モル量に準じる量として「」を付けて「部分モル内部エネルギー」と呼んでいます。