２．イオンによる静電収縮 ～～ ドルーデ-ネルンストの式

19 世紀も後半、電解質溶液の研究が進み、イオンが電荷を持った分子であることが確立しつつあった中で、 イオンの体積の収縮を、電場による誘電体の収縮（静電収縮 electrostriction）という立場から検討したのが、 1894 年のドルーデ P. Drude とネルンスト W. Nernst の研究でした。 当時ドルーデはライプチヒ大学にいて、 オストワルドのもとで電解質溶液の研究をしていたネルンストから、 当時話題になっていたイオンの体積の収縮の問題を教えられ、 この研究に結実したようです。 たぶん物理の方にはドルーデは金属の自由電子モデル（1900 年）でおなじみでしょうが、 この研究は金属の自由電子モデルのヒントになったのかもしれません。

２-１．イオン溶液の誘電体モデル

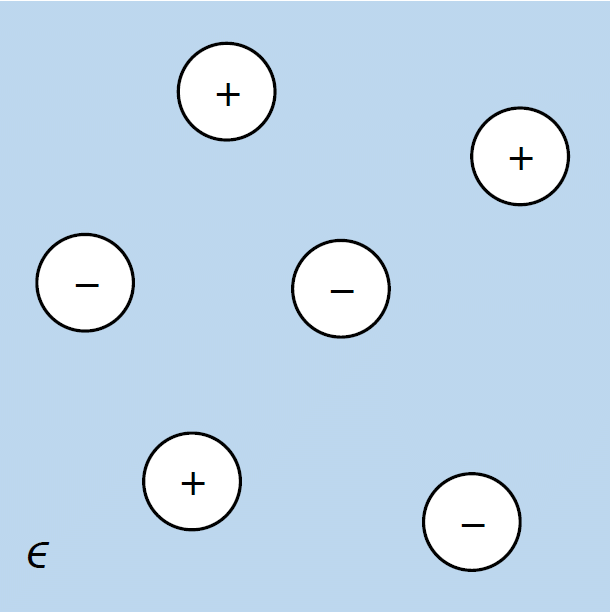
図 2-1. 電解質溶液の誘電体モデル

当時すでに、イオンが電荷を持った分子であるということが、 電池や電気伝導度の研究などからほぼ確立されつつありました。 ドルーデたちは電解質溶液が、正負のイオンが全体として中性を保ったまま、 溶媒中にばらまかれた状態であると考えました（図 2-1）。

さてこの時、溶媒はイオン間の電気力線に貫かれた状況に置かれます。 ここでドルーデたちは溶媒を、コンデンサーで帯電した極版の間に置かれた誘電体のようなものだと見なして論を進めます。 当時すでに（圧縮されて誘電率が増加するなら）、 分極した誘電体は収縮する（静電収縮 electrostriction）ことが分かっていました。 これを先のイオンの体積の収縮の問題に適用しようとしたわけです。 ミョウバンなどの水和結晶の生成や錯イオンなど ”化学的”な知識が豊富な人であれば、 まるで電気回路のパーツのように溶液を扱うのには抵抗があったでしょうが、 そうした背景からネルンストはともかく、ドルーデは自由であったようです。

こうしたモデルは今日ではあまりにも当たり前に見えますが、 当時としては非常に思い切ったモデル化だったでしょう。 そして 30 年後に現れることになるデバイ-ヒュッケル理論（1923 年）などとちがい、 イオン間の相互作用の問題ではなく、 当初はイオンの周りの溶媒を取り扱うモデルとして登場したのは興味深いところです。 ただしそのためには、イオンと誘電体の境界の問題、 分子モデルと連続体モデルの接続の問題と向き合う必要があります。 ドルーデたちは、イオンが球形（ここでは半径 \(r_0\) としておきます）の分子コアを持つものとし、 溶媒の側の分子コアの存在は無視して連続体と考えます。

２-２．静電エネルギーとイオンの化学ポテンシャル

ドルーデとネルンストによる静電収縮の議論を紹介する前に、 誘電連続体モデルに基づく、イオンの静電エネルギーについての、今日、標準的と思われる議論を振り返っておきましょう。

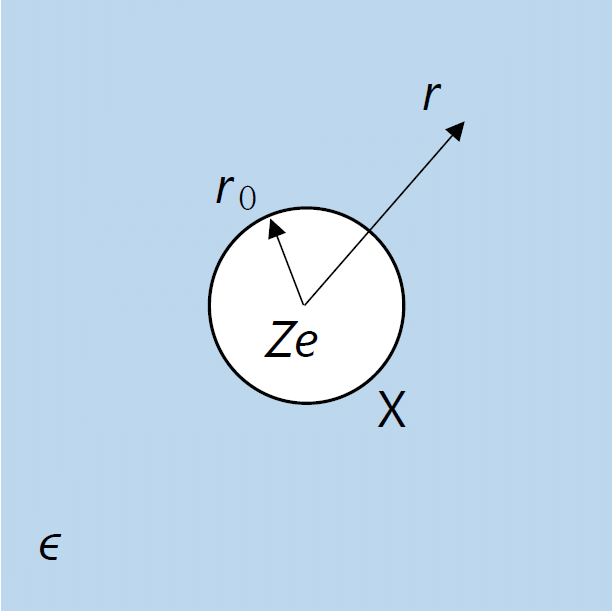
図 2-2. 半径 \(r_0\) のコアを持つ、価数 \(Z\) の球形のイオン X の周りの静電場を考える。

電荷 \(q\) から \(q\) 本の電気力線が湧き出して （\(q \lt 0\) であれば吸い込まれる）、 電気力線は電荷がなければ保存されます。 電束密度 \(D\) は、単位面積当たりの電気力線の数に相当します（SI 単位は C m^-2）。 ですから価数 \(Z\) の球形のイオン X の中心から距離 \(r\) 離れたところの電束密度 \(D(r)\) は、 次式で与えられます（\(e\) は素電荷）：

\begin{equation} D(r) = \frac{Ze}{4 \pi r^2} \label{eq:DaroundI} \end{equation}

電気力線は電場の幾何学的な形状を表しますが、そこには電場の強さがともないます。 電場の強さは電気力線１本あたりに働く張力とみることができ、SI 単位は N/C = V/m になります。 真空中で電場の強さは電束密度に比例し、 またたいていの場合、液体中でも電場の強さは電束密度に比例するとみなせ、 電束密度を \(D\)、電場の強さを \(E\) とすると、 次式が成りたちます。

\begin{equation} E = D/\epsilon \label{eq:lindielec} \end{equation}

通常、電場の強さ（あるいは電圧）を変化させて電束密度（あるいは電荷）を測定するので、 比例係数（\(1/\epsilon\)）は逆数の形で与えられ、 \(\epsilon\) を誘電率と呼びます（SI 単位は C m^-2/(V/m) = F/m）。 このおはなしでは、電荷を与えた時・変化させた時のエネルギーや密度を考えるので、 電束密度 \(D\) がむしろ主役になります。 誘電体（絶縁体）の誘電率と真空の誘電率 \(\epsilon_0\) = 8.854187817... × 10^-12 F/m の比を比誘電率 \(\epsilon_\mrm{r}\) と呼び、 シクロヘキサンなどの無極性溶媒では 2~3 程度、極性溶媒のアセトニトリルで 35、水では 80 程度になります。

\begin{equation} \epsilon = \epsilon_\mrm{r} \epsilon_0 \label{eq:permittivity} \end{equation}

さて単位体積当たりに蓄えられる静電エネルギー \(u_\mrm{el}\) は、 平行平板コンデンサーの話でも登場しますが、 電気力線あたりの電場の強さで与えられ、次式のように表されます：

\begin{equation} u_\mrm{el} = \frac{1}{2} ED = \frac{D^2}{2 \epsilon} = \frac{\epsilon E^2}{2} \label{eq:edens} \end{equation}

イオンの化学ポテンシャル \(\mu_\mrm{X}\) は、 電束密度（電荷）0 の状態の X の化学ポテンシャル \(\mu_\mrm{X}(0)\) に、 静電エネルギーを加えたものになります。 誘電率が一定であるとし、イオンのコア（半径 \(r_0\)）の外部について、静電エネルギーを積分することで次式（ボルンの式）を得ます （ボルン M. Born 1920。 元祖ボルンはこれをエンタルピーと同一視しましたが、自由エネルギーに対応します）：

\begin{equation} \Delta_\mrm{el} \mu_\mrm{X}(Ze) = \int_{r_0}^\infty \frac{D(r)^2}{2 \epsilon} \rmd \vec{r} = \int_{r_0}^\infty \frac{1}{2 \epsilon} \frac{Z^2 e^2}{(4 \pi r^2)^2} 4 \pi r^2 \rmd r = \frac{Z^2 e^2}{8 \pi \epsilon r_0} \label{eq:muion} \end{equation}

ここで \(\Delta_\mrm{el} Y(q)\) は、 電荷 \(q\) を持つ状態の量 \(Y(q)\) と電荷をもたない状態の量 \(Y(0)\) との差 \(Y(q) - Y(0)\) を表すものとします。

以上では誘電体側の静電エネルギーに注目しましたが、 イオンの電位に注目した導出もよく行われます。 電荷 \(q\) を持つ半径 \(r_0\) の球の表面の電位 \(\phi(q)\) は次式で与えられます：

\begin{equation} \phi(q) = \frac{q}{4 \pi \epsilon r_0} \label{eq:ipot} \end{equation}

ここに微小な電荷 \(\rmd q\) を加える時の可逆的な仕事は \(\phi(q) \rmd q\) であり、 電荷を \(Ze\) にまでするのに必要な仕事は、イオンの化学ポテンシャルに対する静電的な寄与を与えます：

\begin{equation} \Delta_\mrm{el}\mu_\mrm{X}(Ze) = \int_{0}^{Ze} \frac{q}{4 \pi \epsilon r_0} \rmd q =\frac{Z^2 e^2}{8 \pi \epsilon r_0} \label{eq:muionx} \end{equation}

やっている中味は誘電体のエネルギーの計算と同じですが、 局所的なエネルギー密度を見なくてよいので、化学者にはこちらの方が人気があるようです。

実際に溶媒が水の場合、イオンにどの程度の静電エネルギーが期待できるか計算してみると、 素電荷 \(e\) は1.60 × 10^-19 C、 真空の誘電率 ε₀ は 8.85 × 10^-12 F/m なので、次のようになります：

\begin{equation} \Delta_\mrm{el}\mu_\mrm{X}(Ze) = \frac{Z^2 e^2}{8 \pi r_0 \epsilon_\mrm{r} \epsilon_0 } = \frac{69.4}{\epsilon_\mrm{r}} \frac{Z^2}{r_0 /\mrm{nm}} \mrm{kJ~mol^{-1}} = 0.89 ~\frac{Z^2}{r_0 /\mrm{nm}} \mrm{kJ~mol^{-1}}~~~ \mbox{水中} \label{eq:muionwater} \end{equation}

ここで水の比誘電率を 78 としました。 よく溶液化学の入門書にありますが、 イオン半径 \(r_0\) を 0.1 nm 程度とすれば、1 価のイオンの静電場のエネルギーは、 真空中では通常の共有結合エネルギー（C-H で 410 kJ/mol 程度）のオーダーになり、 水中では熱エネルギー（300 K で RT = 2.5 kJ/mol）のオーダーになります。

２-３．水の誘電率の圧力依存性とイオンの部分モル体積

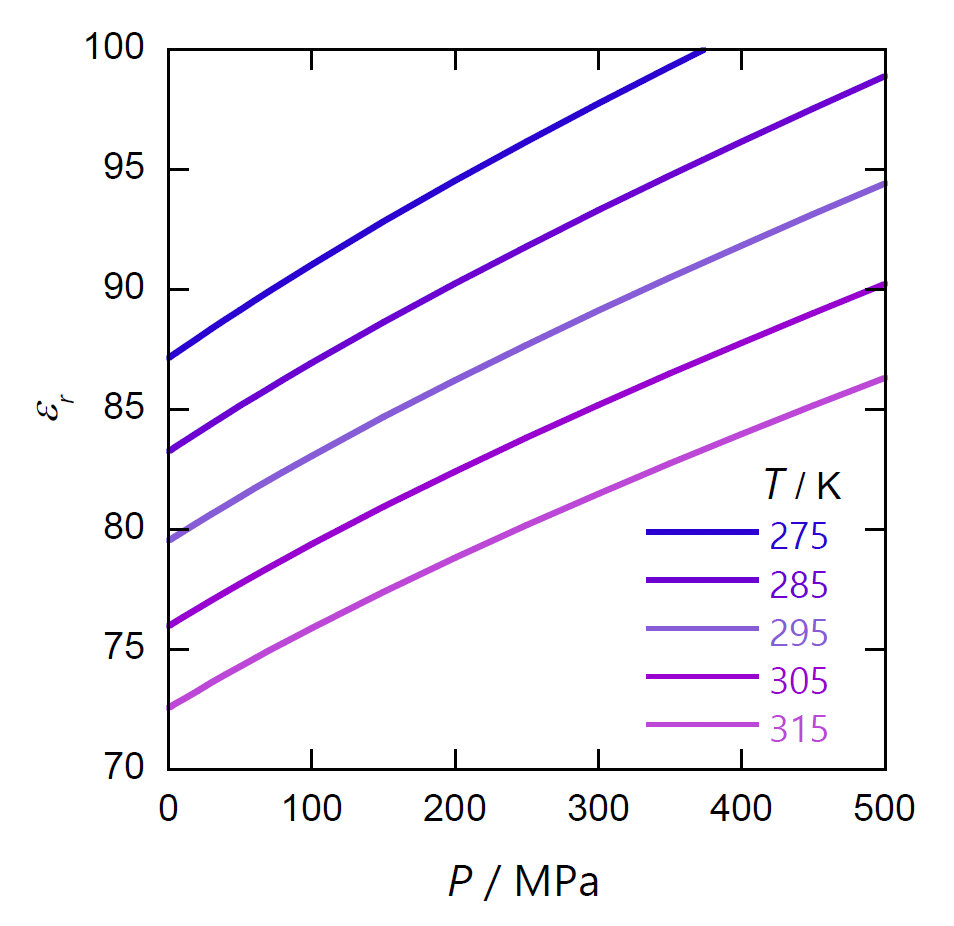
図 2-3. 水の比誘電率の圧力・温度依存性

誘電体に電場をかけた時、誘電体に蓄えられるエネルギー密度が、電束密度の 2 乗に比例し、 電束密度が一定であれば誘電率に反比例し、電場の強さが一定であれば誘電率に比例することを見ました。 ここで注意しておきたいのは、一般に誘電率が温度・圧力の関数になっていることです。

図 1 には、水の比誘電率 \(\epsilon_\mrm{r}\) の圧力・温度依存性を示しました。 常温常圧で水の比誘電率は 80 程度ですが、圧力を 100 MPa（約 1000 気圧）上げると 4 % 程度大きくなり、 温度を 10 K 上げると 4 % 程度小さくなります。 なお水は常圧 4 °C で密度が最大となり、 4 °C 以下で膨張率が負になりますが、 誘電率の温度依存性にはそうした挙動は見られません。

圧力をかけて圧縮した時、誘電率が増加するということは、 電束密度 \(D\) を一定に保っておれば、圧力をかけると静電エネルギーが小さくなることを意味します。 つまりルシャトリエの原理からいうと、 水に働く電場を大きくした時、 静電エネルギーは小さくなる方向に変化しますから、 電場の増加にともなって水は圧縮される、収縮することになります（静電収縮）。 このことは先のイオンの化学ポテンシャルに対する静電的な寄与の表現、 式 \eqref{eq:muion} からも示すことができます。 イオンの部分モル体積は化学ポテンシャルの圧力微分で与えられますから、 電荷 \(Ze\) による部分モル体積の変化は次式のように表されます：

\begin{equation} \Delta_\mrm{el} V_\mrm{X} (Ze) = \pdifA{\Delta_\mrm{el} \mu_\mrm{X} (Ze)}{P}{T} = - \frac{1}{\epsilon^2} \pdifA{\epsilon}{P}{T} \frac{Z^2 e^2}{8 \pi r_0} \label{eq:pvol} \end{equation}

水の比誘電率 \(\epsilon_\mrm{r}\) は 25 °C で 78、\(\partial \epsilon_\mrm{r}/\partial P\) は 37 GPa^-1なので、 数値を評価すると次のようになります。

\begin{equation} \Delta_\mrm{el} V_\mrm{X} (Ze) = - \frac{1}{\epsilon_0 \epsilon_\mrm{r}^2} \pdifA{\epsilon_\mrm{r}}{P}{T} \frac{Z^2 e^2}{8 \pi r_0} = - 0.42 ~\frac{Z^2}{r_0 /\mrm{nm}} ~\mrm{cm^3~mol^{-1}} \label{eq:pvolwater} \end{equation}

ナトリウムイオンのイオン半径は 0.1 nm 程度で、 \(r_0\) をイオン半径に取ると、得られる静電収縮の効果はおよそ 4 cm³ mol^-1。 先に見た有機酸とそのナトリウム塩の部分モル体積の差から評価された 10 cm³ mol^-1 程度の収縮と比して、 けた外れのものではなく、 同程度の値といっていいでしょう （詳細な議論は電荷のない場合との比較が必要なので、ここではこれ以上触れません）。

２-４．ドルーデ-ネルンストによる静電収縮の取り扱い

前節までの今日普通に行われる、イオンの化学ポテンシャルの圧力微分から静電収縮を考える手法は、 イオン溶液の誘電体モデルと静電場の効果 \(\Delta_\mrm{el}\mu_\mrm{X}(Ze)\) の式 \eqref{eq:muion} を認めれば、特に難しいことはありません。 けれども静電収縮を中心に据え、溶媒、水の側の圧縮を正面に据えてかかると、 結構厄介な問題があり、 そのことがドルーデたちの研究が埋もれる結果を招いたように思えます。 ここでは今日的に少し整理した形で、彼らの議論を紹介しましょう。

体積 \(V\)、物質量 \(n\) の水に静電場を働かした時の、 ヘルムホルツエネルギー \(A\) に対する静電場の寄与は、 単位体積当たりに蓄えられる静電エネルギー \(u_\mrm{el}\)（式 \eqref{eq:edens}）を用いて次式のように表されます：

\begin{equation} \Delta_\mrm{el} A = A(D) - A(0) = V u_\mrm{el} \label{eq:ehelmholtz} \end{equation}

以下では \(\Delta_\mrm{el}\) を、 電束密度 \(D\) の状態と 0 の状態の差を表すのに用います。 静電場による水の化学ポテンシャル（\(\mu_\mrm{W}\)）の変化 \(\Delta_\mrm{el} \mu_\mrm{W} \) 次のように表されます（水に関する量であることを強調するため、下付き W を付けておきます）：

\begin{equation} \Delta_\mrm{el} \mu_\mrm{W} = \pdifA{V u_\mrm{el}}{n}{T,V} = \pdifA{u_\mrm{el}}{\rho}{T} \label{eq:dcp} \end{equation}

ここで \(\rho\) は水の密度 \(n/V\) です。 電束密度 \(D\) が一定なら、一般に静電エネルギーは圧縮されると小さくなる、 \(\partial u_\mrm{el}/\partial \rho \lt 0\)、 ことに注意しましょう。

図 2-4. 遠方の電場の及ばない領域との間の、 化学ポテンシャルの釣り合いを考える。

さて、平衡状態ではイオンの周りの電束密度 \(D\) の影響下にある水と、 イオンから遠く離れたところにある水の化学ポテンシャルは等しいはずです。 ですから：

\begin{equation} \mu_\mrm{W}(0, \rho(0)) = \mu_\mrm{W}(D, \rho(D)) = \mu_\mrm{W}(0, \rho(D)) + \Delta_\mrm{el} \mu_\mrm{W}(0, \rho(D)) \label{eq:dcp_eq} \end{equation}

ここで \(\mu_\mrm{W}(D, \rho(D))\) は電束密度 \(D\) の下での化学ポテンシャルで、 あからさまに密度の関数として書きました。 ここで式 \eqref{eq:dcp} を用いると次式を得ます：

\begin{equation} \mu_\mrm{W}(0, \rho(D)) - \mu_\mrm{W}(0, \rho(0)) = -\pdifA{u_\mrm{el}}{\rho}{T} \label{eq:dcp_eq2} \end{equation}

この式は電束密度 \(D\) の下で、水の化学ポテンシャルが \(\partial u_\mrm{el}/\partial \rho (\lt 0)\) 減少し、 その分、密度が \(\rho(D)\) に増加する（体積が収縮する）ことを示しています。 浸透圧の議論で、溶質を加えることで圧力が増加することを思い出していただいてもよいでしょう。

さて \(\Delta_\mrm{el} \mu_\mrm{W}\) が十分小さいとすると、 水の密度の変化 \(\Delta_\mrm{el} \rho\)は、式 \eqref{eq:dcp_eq2} から、次式で評価できます（\(\partial P/\partial \mu_\mrm{W} = \rho\) に注意）：

\begin{equation} \Delta_\mrm{el} \rho = \pdifA{\rho}{\mu_\mrm{W}}{T} [\mu_\mrm{W}(0, \rho(D)) - \mu_\mrm{W}(0, \rho(0)] = -\pdifA{P}{\mu_\mrm{W}}{T} \pdifA{\rho}{P}{T} \pdifA{u_\mrm{el}}{\rho}{T} = -\rho \pdifA{u_\mrm{el}}{P}{T} \label{eq:dden} \end{equation}

いささか持って回った議論をしていますが、 ざっくりいえば、電場による密度変化と化学ポテンシャルの変化についての、 次のような関係式をなぞっているわけです（\(\partial \mu/\partial D = \Delta_\mrm{el} \mu\) としています）：

\begin{equation} \pdifA{\rho}{D}{\mu} = - \pdifA{\rho}{\mu}{D} \pdifA{\mu}{D}{\rho} = - \pdifA{\rho}{\mu}{D} \pdif{u_\mrm{el}}{\rho} =- \pdifA{P}{\mu}{D} \pdif{u_\mrm{el}}{P} =- \rho \pdif{u_\mrm{el}}{P} \label{eq:rhomu} \end{equation}

イオンに電場が存在することで、イオンの周りに集まる溶媒粒子の数 \(\Delta_\mrm{el} n\) は、 各地点における密度の変化 \(\Delta_\mrm{el} \rho(r)\) を積分することで評価でき：

\begin{equation} \Delta_\mrm{el} n = \int_{r_0}^\infty \Delta_\mrm{el} \rho(r) \rmd \vec{r} \label{eq:dnum} \end{equation}

イオンによる体積の収縮は、次式で得ることができます：

\begin{equation} \Delta_\mrm{el} V_\mrm{X} = -\rho^{-1} \Delta_\mrm{el} n \label{eq:dvx} \end{equation}

距離 \(r\) における静電場のエネルギー \(u_\mrm{el}(r)\) は 次式のようになりますから、

\begin{equation} u_\mrm{el}(r) = \frac{D(r)^2}{2 \epsilon} = \frac{Z^2 e^2}{32 \pi^2 \epsilon r^4} \label{eq:ener} \end{equation}

これを式 \eqref{eq:dden} に代入して、式 \eqref{eq:dnum} と 式 \eqref{eq:dvx} から、 静電場による体積の収縮、部分モル体積の変化は次式で与えられます：

\begin{equation} \Delta_\mrm{el} V_\mrm{X}(Ze) = -\rho^{-1} \frac{\rho}{\epsilon^2} \pdifA{\epsilon}{P}{T} \int_{r_0}^\infty \frac{Z^2 e^2}{32 \pi^2 r^4} 4 \pi r^2 \rmd r = -\frac{1}{\epsilon^2} \pdifA{\epsilon}{P}{T} \frac{Z^2 e^2}{8 \pi r_0} \label{eq:vstriction} \end{equation}

こうして溶媒（水）の静電収縮に注目する形でも、 先にイオンの電位に注目することで得た式 \eqref{eq:pvol} と同じ表現を得ることができます。

表紙のページへ