ドルーデとネルンストの静電収縮の取り扱いで、 イオンになった時の体積の収縮について、 少なくとも定性的なレベルでの説明ができます。 しかしそこからさらに踏み出そうとすると、多くの困難があり、 さまざまな試みがなされてきました。 たぶんみなさんご存じのこととも思いますが、 ここでは大きく2つの点を挙げておきます。
おそらく溶液の誘電連続体モデルでの一番のネックは、 非電解質の挙動が説明できないこと、そもそも説明しようとしないことでしょう。 ドルーデたちのモデルで行くと、 イオンに電荷がなければ、溶媒を変えても同じ部分モル体積を示すはずです。 しかし実際には有機溶媒と比べて水中での部分モル体積は一般に小さくなります。 たとえば 25 °C でジエチルエーテルの部分モル体積は四塩化炭素中では 102.6 cm3 mol-1 ですが、 水中では 90.4 cm3 mol-1 と、10 cm3 mol-1 程度小さくなります。 より極性の低い球形のメタン CH4 についても同様で、四塩化炭素中では 51.8 cm3 mol-1 ですが、水中では 34.5 cm3 mol-1 とされています。 この違いは静電収縮による効果とされるものに匹敵します。 こうしたことはすでに 19 世紀末には知られていて、 トラウベなどはドルーデたちの取り扱いに批判的でした(J. Traube, Samml. Chem. Chem-Tech. Vorträge, 4, 330, (1899) )。
今回問題にしている中和反応についていうと、 すでに触れたようにオストワルドの研究は次のように整理できます:
ここで HA は酢酸などのカルボン酸を示し、アンモニウムイオンの表記に合わせて、水素イオンをヒドロニウムイオン H3O+ として表記しました。 このように電荷が消失する中和反応で、大きな体積増加が起きることは静電収縮の結果として整理できるでしょう。
けれどもその大きさには2倍くらいのひらきがあり、事態はそう単純ではありません。 カルボン酸アニオン A- が嵩張る構造なので水酸化物イオン OH- より静電収縮の効果が小さいので体積変化が小さいのでしょうか? でもそれならアンモニウムイオン NH4+ の方がヒドロニウムイオン H3O+ より嵩張るので、 静電収縮の効果が小さいはずではないでしょうか? こうした話になってくると、そもそも電荷のない場合にどれほどの体積変化が現れるのかが問題になってきます。 そこが定まらないと、静電収縮の議論自体が空回りを始めます(往々にして理論は結果論になるものです・・・)。
非電解質の問題、電荷がない場合の部分モル体積の問題を置いておくとしても、 イオンの周りの溶媒を誘電連続体としての扱うには大きな問題があります。

|
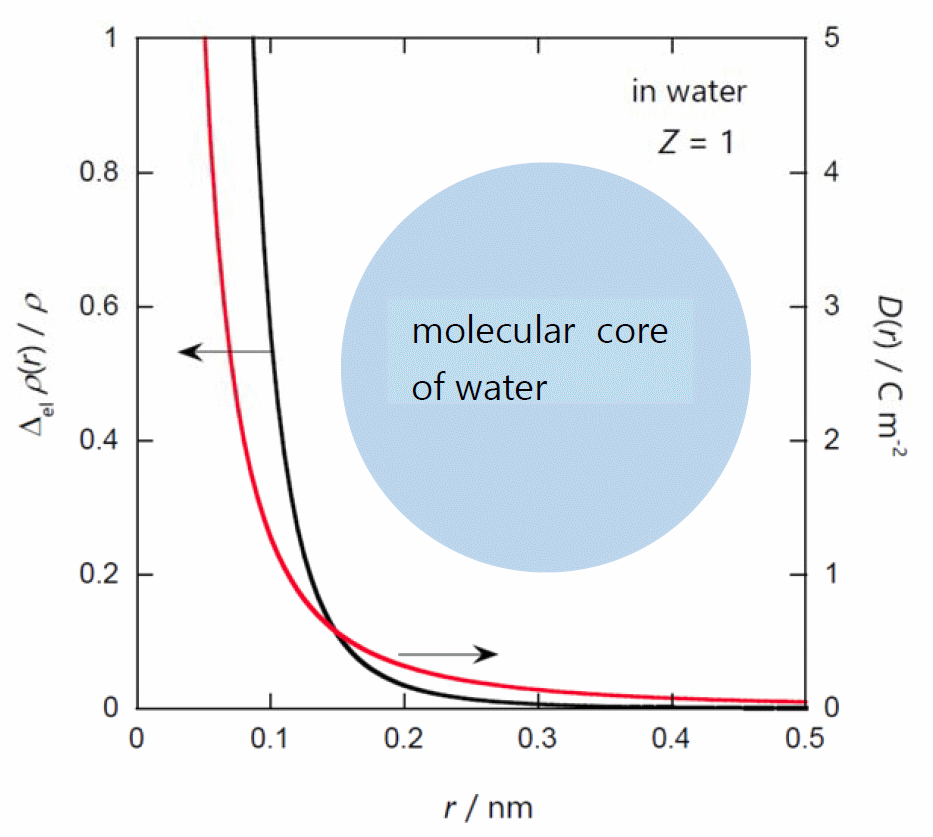
| 図 3-1. 単純な静電収縮理論から予想される、 静電収縮によるイオンの周囲の密度変化 Δelρ(r)/ρ(黒い実線)と 電束密度 D(r)(赤い実線)。 水中、イオンの電荷 1 の場合の結果。 図中の水色の円は、水分子のコアの大きさを示します。 |
実際に静電収縮によってイオン周りの水の密度がどの程度変化するか、 先の取り扱いどおりに求めてみると、 次のような結果を得ます:
\begin{eqnarray} \frac{\Delta_\mrm{el} \rho(Ze, r)}{\rho} &=& - \pdifA{u_\mrm{el}(r)}{P}{T} \\ &=& \frac{1}{\epsilon^2} \pdifA{\epsilon}{P}{T} \frac{Z^2 e^2}{32 \pi^2 r^4} \sim 5.6 \x 10^{-5} \frac{Z^2}{(r / \mrm{nm})^4} \label{eq:ddenx} \end{eqnarray}
図 3-1 に式 \eqref{eq:ddenx} から得られる、電荷が 1 のイオン近傍の水の密度変化を示します。 距離が 0.4 nm 程度であれば、0.2 % 程度圧縮されるぐらいで、 微小量としての取り扱いはそんなに悪くないでしょう。 でもそれよりイオンに近づくにつれ、想定される圧縮の度合いは急速に大きくなっていきます。
先にナトリウムイオンを想定して、 イオンのコアの半径を 0.1 nm 程度として静電収縮が 4 cm3 mol-1 起きることになることを見ました。 しかしその時、 イオンのコア近傍の水の密度は5割以上増える勘定になります。 水の密度が 1.5 g/cm3 となれば、これは液体ではなく氷(高圧氷)です。 あるいは電場の強さを考えると、電束密度 \(D\) は 0.1 nm で 1.3 C/m2 になり、 水の比誘電率を 80 ぐらいとすると、電場の強さ \(E\) は 2 GV/m ぐらい。 普通なら絶縁破壊を起こす電場で、 誘電体として扱えるかどうか問題です。 またマグネシウムなど 2 価のイオンであれば、この 4 倍の密度増加、電場の強さを想定することになり、 いよいよぶっ飛んだ話になってきます。 淡々とイオンの静電収縮を計算する取り扱いの背後には、 とんでもない想定が潜んでいるのです。
さらに大きな問題は、イオンと誘電連続体としての溶媒の境界線をどこに引くのかという問題です。 図 3-1 に水分子のコアの大きさ(およそ直径 0.3 nm の球。直径の 3 乗が水のモル体積相当)を示してみました。 こうした分子からなる液体が、 イオンのコアの半径の外部の空間をすきまなく埋め尽くすと考えるのはとんでもない話でしょう。 少なくとも先に考えたような、イオンから 0.1 nm 離れた地点の水の誘電率やその圧力微分を議論するのは、 荒唐無稽と言われても仕方ありません。 ですからナトリウムイオンの場合で言えば、 イオンからせいぜい 0.4 nm 以遠の水を連続体として想定するのが、 密度変化の大きさ( Δelρ(r)/ρ = 0.0022)からしてもいいところでしょう。 ただしそうすると得られる静電収縮の大きさは 1 cm3 mol-1 程度とお寒いものになってしまいます。 実験的に得られている静電収縮の評価には、0.4 nm よりさらにイオン近傍の問題に踏み込む必要が出てきます。
こうしたイオン近傍の問題は古くから認識され、さまざまな提案がなされてきました。 連続体近似の範囲内でも、静電収縮による誘電率の変化を組み込んで、 非線形性を考慮する試みもあります(Frank の取り扱いは有名です)。 また強電場の下での誘導飽和を考慮すれば(磁性の場合の強磁性体を考えてもらえばよいでしょう)、 実効的な誘電率が減少し静電エネルギーが増加して大きな静電収縮が期待できるので、ここに期待する向きもあります。 あるいは化学者に人気があるのは、ボルンの式でよく見かけますが、 イオン半径に溶媒のサイズの寄与を組み込んで、実効半径に読み替えようという考えです (そもそも ”イオン半径” というものが、 配位数などに依存する実効的なものです)。 しかしいずれにせよ、連続体の近似が破綻する領域をもっともらしく取り繕う話にしかならないでしょう。 またこの連続体の近似が破綻することが、 前節で挙げた非電解質の部分モル体積の問題でもあるわけです。
連続体としての取り扱いが破綻することは、 安易に誘電率に寄りすがるアプローチから脱却する必要を強く示唆します。 それには従来の誘電率の議論からさらに踏み出すことが求められるわけですが、 現状はかなり残念な状況のようです。 ぼくが若いころは、まだオンサーガー Onsager やカークウッド Kirwood の理論などとそれなりに取り組んでいる人を見かけたものでした。 でも最近はほとんど見かけませんし、 若い人たちと話しているとクラウジウス-モソッティの式すら怪しいことがあるようです。 こういった過去の研究ときっぱり道を分かつところから、 本質的に新しい展開があるのかもしれませんが、 老人は何とも心もとないものを感じてしまいます。
イオン近傍の高電場の存在は、すでにドルーデたちも考えていたところです。 彼らは静電収縮の大きさが物質によって大きく変化しないこと (カルボン酸の酸会合の体積変化があまり変わらないこと)に注目しました。 彼らはこの差異のなさから、イオン近傍では誘電率が極めて大きくなって静電収縮の効果が減少し、 静電収縮がイオンの大きさ、種類に依存しなくなると考えました。 分子構造やそもそもの素電荷の大きさ(あるいはアボガドロ定数)なども定かでなかった当時(1894 年)としては、 当然の判断だったのかもしれません。 逆に、彼らは静電収縮から素電荷の大きさを推定することを考えていたようです。