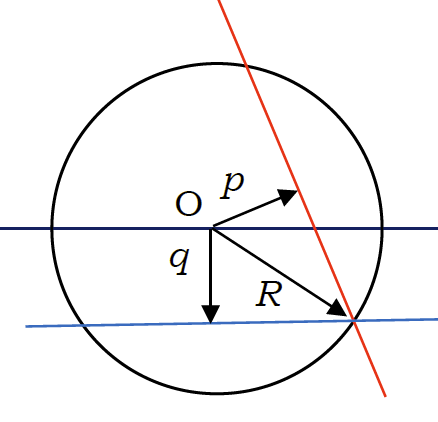
 図2-0. 2本の直線の交点が半径 \(R\) の円内にあるには、\(p, q \lt R\) でないといけない。
図2-0. 2本の直線の交点が半径 \(R\) の円内にあるには、\(p, q \lt R\) でないといけない。
先に平面上の直線の重み、測度について、ヘッセの標準形を考えて、\(\rmd p \rmd \theta\) というのが適切だということを見ました。 このことを押さえた上で、 最初に考えた問題、 でたらめに引いた2本の直線が、ある角度で交わる確率を考えてみましょう。
前にも取り上げましたが、 「2本の直線は必ず交わると考えてよい。 でたらめに引いているのだから、交差する角度は360°同じ確率で出現する」 という主張は、2番目のポイント「交点を見出す」手順で、 「平面上のどこでもいいから交わってさえおればよい」 そして 「交わってさえおれば、同じだけの重みをもっている」 と考えていることに相当します。 この交点を見出す確率、交点の重みを検討する必要があるのです。
 図2-0. 2本の直線の交点が半径 \(R\) の円内にあるには、\(p, q \lt R\) でないといけない。
図2-0. 2本の直線の交点が半径 \(R\) の円内にあるには、\(p, q \lt R\) でないといけない。
われわれが、2直線の交差する角度を調べるとき、 平面上のある領域に注目して、そこに存在する交点について、その交差角を調べます。 ただでたらめに直線を2本引いただけでは、その交点は平面上いたるところに散らばってしまいます。 そこで原点を中心とする半径 \(R\) の円内にある2直線の交点に注目することにします。 この円内で交わる2本の直線をヘッセの標準形を用いて \((p, \theta)\) と \((q, \varphi)\) で表せば、 図に見るように \(p, q \lt R\) でないといけない。 つまり、\(p, q \lt R\) である2本の直線の交点が半径 \(R\) の円内にある場合について、 そのなす角度の重み、測度を検討すればよいわけです。
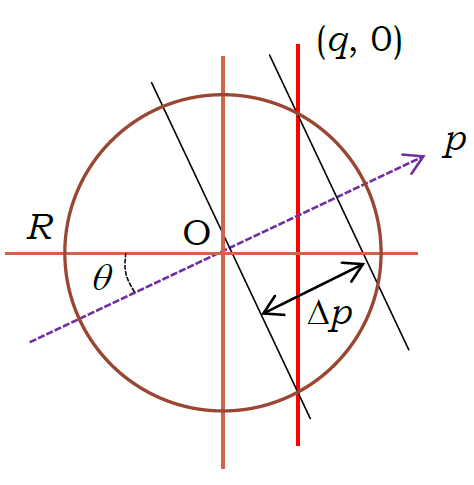
図2-1. 2本の直線の交点。 直線\((q, 0)\) (赤い線)と直線 \(p, \theta\) の交点が、 半径\(R\) の円内にある\(p\)の範囲を求める。
話を簡単にするために、2本の直線の内 \((q, \varphi)\) については、角度を \(\varphi = 0\) に固定して考え、 \((p, \theta)\) については、便宜的に \(0 \le \theta \lt \pi\)にとり、 \(p\) が負の値をとってもよいことにします (つまり\(p\)を原点からとった\( \theta\) 方向の数直線上の位置座標と考えます)。 すると図に見るように、直線 \((q, 0)\) と交わる直線 \(p, \theta\) について、 次の条件が成立します。
\begin{equation} q \cos \theta - \sqrt{R^2 - q^2} \sin \theta \lt p \lt q \cos \theta + \sqrt{R^2 - q^2} \sin \theta \label{eq:cross_pcond} \end{equation}
2直線の交わる角度は \(\theta\) になりますから、角度 \(\theta\) で交わる確率は\(p\) が取る値域の広さ \(2 \sqrt{R^2 - q^2} \sin \theta\)、角度 \(\theta\) についていえば \(\sin \theta\) に比例し、 交わる角度の分布関数\(f(\theta)\)は次式になります( \(0 \le \theta \lt \pi\))。
\begin{equation} f(\theta) = \frac{1}{2} \sin \theta~~~(\rm{in~circle}) \label{eq:cross_theta} \end{equation}
つまりある領域の中に存在する2直線の交点に注目するなら、 90°で交わる確率は、45°で交わる確率の \(\sin 90^{\circ}/\sin 45^{\circ} = \sqrt{2}\) 倍になるわけです。 また2直線 \((p, \theta)\) と \((q, \varphi)\) が、 半径\(R\) の円内で交わる確率は、
\begin{equation} \int_0^{\pi} \rmd \theta \int_0^{R} \rmd q 2 \sqrt{R^2 - q^2} \sin \theta = \pi R^2 \label{eq:cross_incirc} \end{equation}
ですから、\(\int \rmd \theta \int \rmd q 2R = 2\pi R^2\) なので、 1/2 ということになります。
事態を整理すると、\(p, q \lt R\) である2本の直線のなす角を求めれば、 360° すべて同等の確率で出てくるけれど、 交点が半径\(R\) の円内にある直線の組に限れば(これは全体の1/2)、 2直線のなす角の出現確率は、その正弦に比例する。 発生させた2直線の組み合わせだけに注目すると、 交差角は等方的に分布するのですが、 交点が均一に分布する領域に絞って考える、 つまりそこで交差する場合を尽くしてみると式 \eqref{eq:cross_theta} が成立するのです。
このあたりの事情をはっきりさせるために、“実験”してみましょう。 ヘッセの標準形で直線を表示し、\(0 \le p \lt 1\)、\(0 \le \theta \lt 2 \pi\) の値域で一様乱数を発生させ、 多数の直線を生成させて、 そこから2本の直線を取り出して、両者の交点を計算します。 このように設定すると、原点においた半径 1 の円内には、均一に2直線の交点が分布するはずです。 もし交差角\(\varphi\) の出現確率が式 \eqref{eq:cross_pcond} で予想されるように、 \(\sin \varphi\) に比例するなら、 余弦 \(\cos \varphi\) の出現確率は\(\varphi\) によらず一定になるはずです(交差角として鋭角側、\(0 \le \varphi \lt \pi/2\)を取ります)。 10000 本の直線を発生させた時に得られた 10000 × (10000 - 1)/2 = 49995000 個の交点について、 交差角\(\varphi\) の余弦 \(\cos \varphi\) 分布を、半径 1 の円内、円外も含めた全交点について調べた結果を図に示します。 円内に注目すると、分布は式 \eqref{eq:cross_pcond} で予想されるように、余弦の分布は一定になっています。 一方、円外も視野に入れると、交差角の分布は等方的に振舞っています。
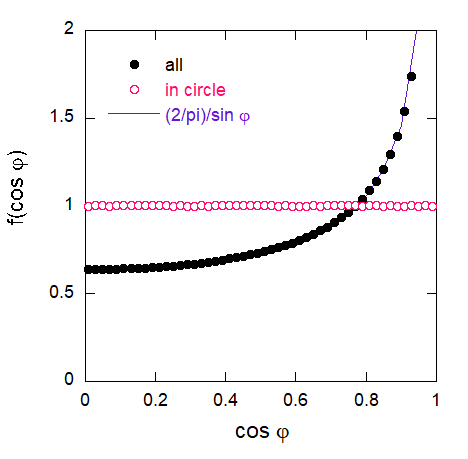
図2-2a |
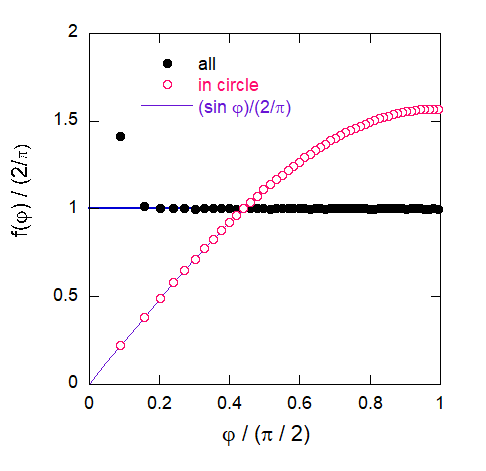
図2-2b |
| 10000 本の\(0 \le p \lt 1\) のランダムな直線を発生させ、 直線間の交差角\(\varphi\) (鋭角側を取る)の出現頻度を求めた結果。 半径 1 の円内の交点(全部で49995000点の交点のうち25012790点で全体の0.5003で、式\eqref{eq:cross_incirc}の評価通り)については、 交差角の余弦\(\cos \varphi\) の出現頻度は一定。 平面上の全領域についての交点をとれば、 交差角 \(\varphi\) の出現頻度は一定。 | |
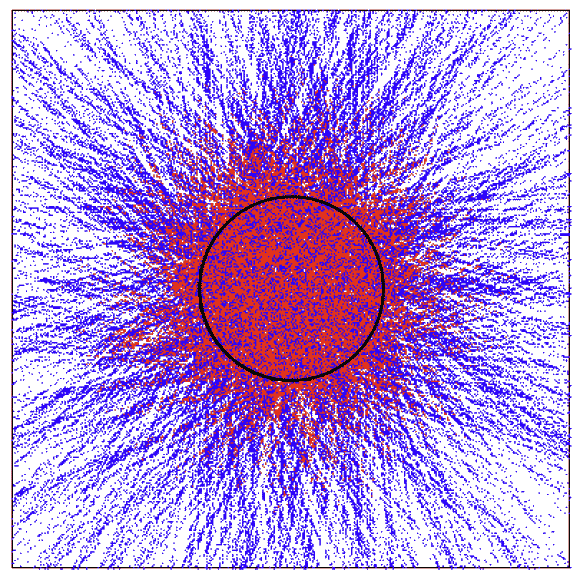 図2-3. \(p \lt 1\) で発生させた1000本の直線の間の交点のプロット。
交差角が45° 以上の交点を赤、45° 以下の交点を青で示す(交差角としては鋭角側を取る)。
図中黒い実線で示す半径1の円内には、
交点が均一に分布し(赤の割合が\(1/\sqrt{2}\))、
円外では円から離れるに従って青の割合が増えていく
(円の中心からの距離が 2.61 (= \(1/\sin (\pi/8)\))以遠では、
青のみ)。
図2-3. \(p \lt 1\) で発生させた1000本の直線の間の交点のプロット。
交差角が45° 以上の交点を赤、45° 以下の交点を青で示す(交差角としては鋭角側を取る)。
図中黒い実線で示す半径1の円内には、
交点が均一に分布し(赤の割合が\(1/\sqrt{2}\))、
円外では円から離れるに従って青の割合が増えていく
(円の中心からの距離が 2.61 (= \(1/\sin (\pi/8)\))以遠では、
青のみ)。
このことは、交点の交差角が45°以上か以下かで色分けした、 図を見ていただければより納得いただけるでしょうか。 半径 1 の円内では、均等な分布が実現していて、 どの部分を取っても交点の交差角が45°以上となる比率は \(1/\sqrt{2}\) です。 一方円外では、交点の交差角が45°以上となる比率は均一ではなく、 外部に行くほど低くなっていきます。
先ほどの2直線が交わる角度の出現確率の評価で、 \((p, \theta)\) と \((q, 0)\) が円内で交わる重み(測度)を考えました。 この重みをそれぞれの直線について考えてみると、 交わっている状態での直線\((p, \theta)\) の重みと、 直線\((q, 0)\) の重みとが等しいと見なせるはずです (いわば図形の合同を考えればよいでしょう)。 ここで図形の重みとして、 これまではヘッセの標準形から \(\rmd p \rmd \theta\) というものを考えていたのですが、 直線上の長さ\(s\)に焼きなおすことを考えると、 \(p\)に対応する区間の大きさが \(2\sqrt{R^2 - q^2} \sin \theta\) つまり、直線\((q, 0)\)上の区間の長さ(図2-1の弦の長さ)に \(\sin \theta\) をかけたものに対応していることがわかります。
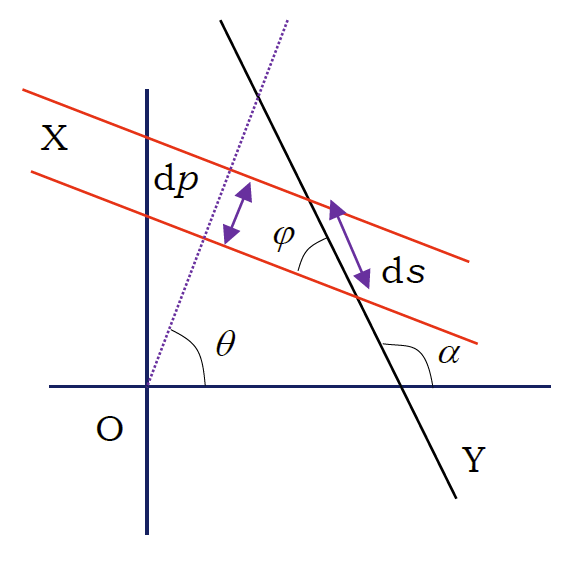
図2-4. 直線Xの測度と交差する線Y上の距離\(s\)を座標に取った測度。 \(\varphi = \pi/2 - (\alpha - \theta)\) より \(\rmd \varphi = \rmd \theta\)に注意
これをもう少し一般的にして、 図2-4 のように直線 X に 直線 Y が、角度 \(\varphi\) で交わっている状況を考え、 直線 X がヘッセの標準形を用いて \((p, \theta)\) で表されているとします。 ここで Y 上のある点からの距離 \(s\) で、X との交点を表現したとすると、 測度について次の関係が成り立つことになります。
\begin{equation} \rmd p \rmd \theta = \sin \varphi \rmd s \rmd \varphi \label{eq:cross} \end{equation}
角度 \(\varphi\) で交わる直線の測度が、 一方の直線上の長さに\(\sin \varphi\) をかけたものに比例する。 さきほどは半径\(R\)の円内の交点に注目したわけですが、 直線上のある領域(\(\rmd s\))に注目して考えてみても同様に、 90°で交わる確率は、45°で交わる確率の \(\sqrt{2}\) 倍になるわけです。
以上の議論は、 曲線と直線が交わる場合に拡張できます。 直線 Y を交点における曲線の接線とし、 \(s\) を曲線の長さと考えます。 すると先の議論がそのまま使え、 同様に式 \eqref{eq:cross} が成立します。
曲線の場合に拡張したとき、 閉じた平面図形に関わって、興味深い問題が出てきます。 ここでは特に凸体、その中の2点を結ぶ線分が必ずその図形の中にある、 つまり凹んだ部分のない図形を考えます (直線が何カ所で交わるかは重要な点ですが、ここではこれ以上立ち入りません)。
凸体と交わるような直線全体について、 その測度は凸体の周囲の長さ\(L\)に比例します。 これは式\eqref{eq:cross} を積分した次式を見れば明らかでしょう。
\begin{equation} \int {\rmd s {\int_{0}^{\pi} {\rmd \varphi \sin \varphi} }} = 2L \label{eq:peri} \end{equation}
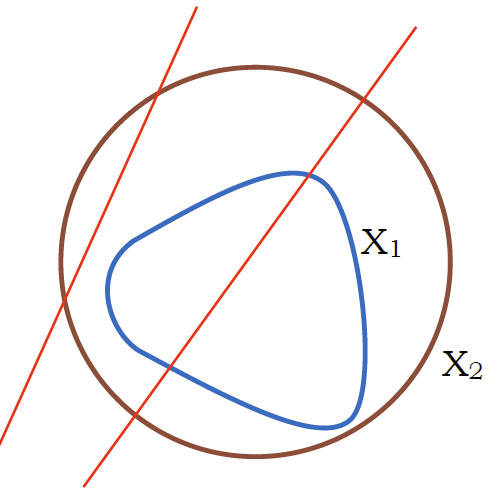 図2-5. 凸体X2 と交わる直線が凸体X1 と交わる確率は、
X2 と X1 の周囲の長さの比に等しい。
図2-5. 凸体X2 と交わる直線が凸体X1 と交わる確率は、
X2 と X1 の周囲の長さの比に等しい。
ここから、凸体 X1 が 凸体 X2 の内部にある時、 凸体 X2 と交わる直線が X1 と交わる確率 \(P\) が、 両者の周の長さの比になるという、 クロフトン Crofton の式が導かれます。
\begin{equation} P = L_1/L_2 \label{eq:crofton} \end{equation}
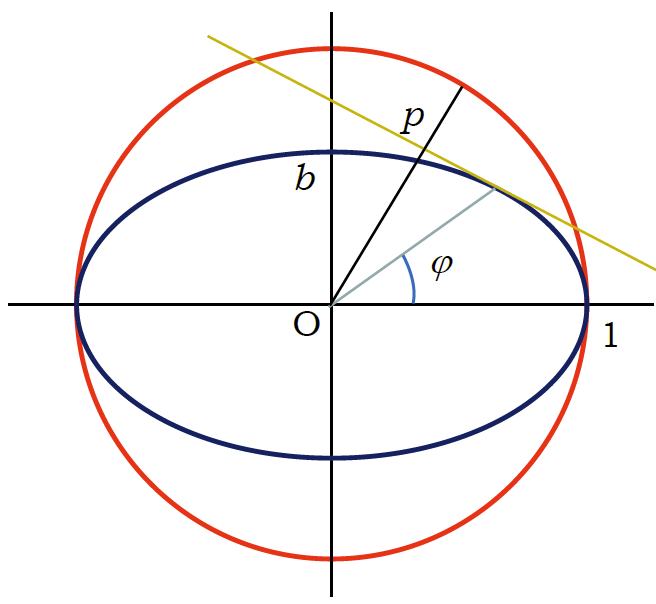
図2-6. 半径 1 の円に内接する楕円の周長をモンテカルロ法で求める
この式は結構使い出のある式なのですが、 少し抽象的な印象があるので“実験”してみましょう。 図のように半径 1 の円の中に、長径 1、短径 \(b \)(\(b \le 1\))の楕円が内接しているとして、 楕円の周の長さをモンテカルロ法で求めます。
でたらめに直線を引いたとき、円と交わる確率と楕円に交わる確率 \(P\) が周長に比になるというのですから、 楕円の周の長さは \(2\pi P\) になるはずです。 パラメーター表示で楕円は次式で表されます
\begin{equation} x = \cos \varphi ,~~~ y = b \sin \varphi \label{eq:elipx} \end{equation}
円と交わるようにでたらめな直線を発生させ、 楕円と交わる確率を求めてみます。 円と交わるようなでたらめな直線を発生させるには、 ヘッセの標準形で、 \(p \le 1\) となるように一様乱数と、 等方的な単位ベクトル \(\vec{e}\)を作ればよいわけです。 この直線が楕円と接する時の \(p\) の値が、 \(\vec{e}\)と垂直な方向について、円と交わる直線が楕円と交わる確率に相当します。 接点の座標を\((\cos \varphi, b \sin \varphi)\) であるとすると、 接線の向き\(u\)は\((-\sin \varphi, b \cos \varphi)\) で、 これが\(\vec{e} = (e_{x}, e_{y})\)と直交する条件は、次式で与えられます。
\begin{equation} -e_x \sin \varphi + b e_y \cos \varphi = 0 \end{equation}
ここから接点について次の関係が得られます
\begin{eqnarray} \sin^2 \varphi &=& \frac{b^2 e_y^2}{e_x^2 + b^2 e_y^2} \\ \cos^2 \varphi &=& \frac{e_x^2}{e_x^2 + b^2 e_y^2} \end{eqnarray}
したがって楕円の接線の\(p\)の値は、接点の位置ベクトルと\(\vec{e}\)の内積を取って、 次式で表されます
\begin{eqnarray} p &=& \cos \varphi e_x + b \sin \varphi e_y \\ &=& \sqrt{e_x^2 + b^2 e_y^2} \label{eq:elipy} \end{eqnarray}
ですから計算に当たっては、ランダムな等方的な単位ベクトル\(\vec{e}\)を発生させ、 式 \eqref{eq:elipy} を計算して、その平均を取ればよいわけです。 表2-1に100000回、等方的な単位ベクトルを発生させて得た結果を示します。 計算結果は後に紹介する弧長の公式(式 \eqref{eq:elipz})を数値計算した結果と一致して、 式\eqref{eq:crofton}が成立していることが分かります。
| \(b\) | 0.25 | 0.5 | 0.7 |
| MC | 2.148 ± 0.008 | 2.424 ± 0.005 | 2.692 ± 0.003 |
| rigorous | 2.14460544... | 2.42211205... | 2.69118449... |
さて楕円の周の長さ\(L\)は、 次の積分で計算することができます(第2種完全楕円積分)。
\begin{eqnarray} L &=& \int_0^{2 \pi} {\sqrt{x_\varphi^2 + y_\varphi^2} \rmd \varphi} \\ &=& 4 \int_0^{\pi/2} {\sqrt{\sin^2 \varphi+ b^2 \cos^2 \varphi} \rmd \varphi} \label{eq:elipz} \end{eqnarray}
式\eqref{eq:elipy} はもっぱら確率に注目して計算したわけですが、 やっていることは式\eqref{eq:elipz} のモンテカルロ計算と同等であるのは面白いところです。