
共沸現象について、まず復習しておきましょう。
混合物では一般に沸点(加熱・減圧していって蒸気(泡)が発生する温度・圧力)と露点 (冷却・加圧していって液体(露)が発生する温度・圧力)は一致しません (過熱・過冷却は考えません。なお混合液体では「沸点 boiling point」ではなく「泡点 bubble point」と呼ばれることが多いようですが、 ここでは沸点で通します)。 また一般に、液体と蒸気の組成は一致しません。
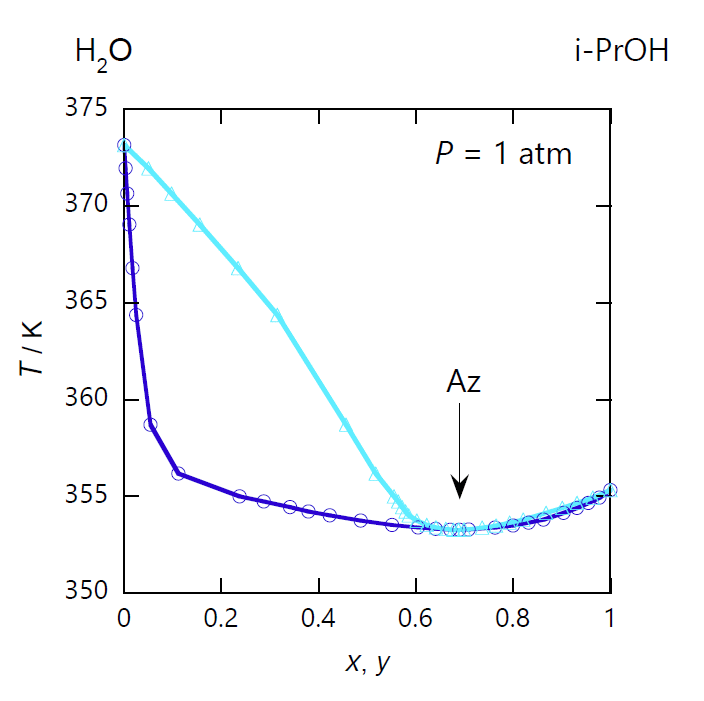
図 0-1 に示すのは、病院などで消毒によく用いられる 2-プロパノール(イソプロパノール)-水系の気液平衡の典型的な相図です (業界では低沸点の物質を第1成分に取るのがフツウのようです)。 まず図 0-1a の 1 気圧での沸点・露点曲線を見てみましょう。 2-プロパノール(沸点 82.2 °C)と水(沸点 100 °C)を混ぜると、 両者の沸点より低い温度で沸騰するようになります。 同様に蒸気の凝縮する温度(露点)も低くなります。 そして 80 °C で沸点と露点は一致して、 最小値となります。 これが共沸点で、共沸点では液体と蒸気の組成が等しく、2-プロパノールのモル分率 \(x\) は、 液相でも気相でも 0.69(質量分率 88 mass%)になっています。
図 0-1a では圧力を一定にして、 露点、沸点を見たわけですが、 図 0-1b に示すのは、温度を 80 °C に保って、 凝縮、沸騰の際の蒸気圧を調べた結果です。 先の圧力一定での凝縮、沸騰温度と逆に、 2-プロパノール(蒸気圧 92 kPa)と水(47 kPa)を混ぜると、 両者の蒸気圧より高い圧力で沸騰するようになります。 同様に蒸気の凝縮する圧力も高くなります。 そして蒸気圧が最大となるところでは、 気相と液相の組成が等しく、温度を 1 気圧での共沸温度に設定しているので、 等圧条件で得られる共沸濃度と一致します。
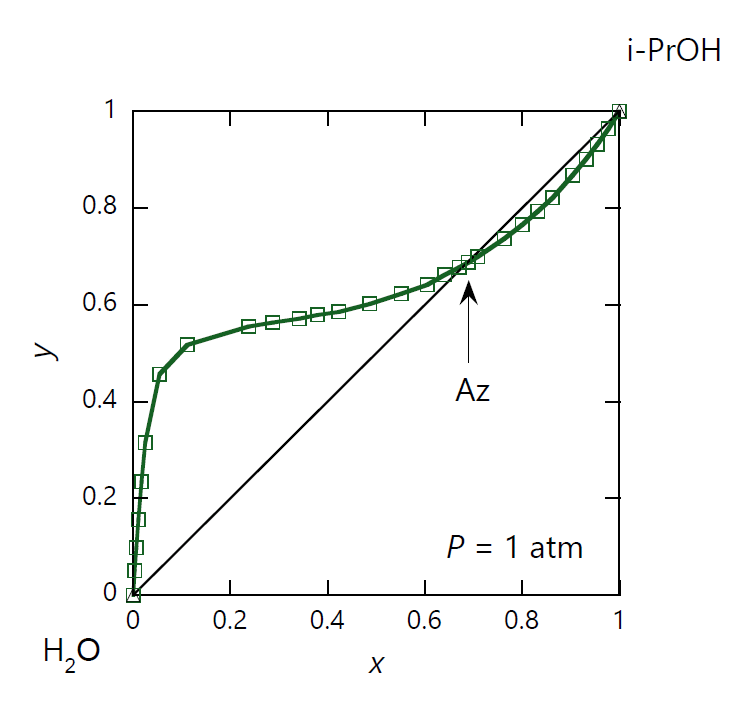
凝縮・沸騰する際の蒸気中の 2-プロパノールのモル分率 \(y\) を、 液相中のモル分率 \(x\) についてプロットしたのが図 0-1c です。ここでは圧力一定で見ていますが、 温度一定の条件でも同様の図が得られます。 共沸点の \(x=y=0.69\) を境に、液相と気相の 2-プロパノールの分配比 \(y/x\) は逆転し、 水の富んだ組成では2-プロパノール、2-プロパノールの富んだ組成では水が、それぞれ気相に多く分配されることになります。 いわば ”よそ者” を液相から疎外する傾向にあるわけです。 こうした成分間の性格が、「正の共沸」の背後にあるといってよいでしょう。

|

|

|
| 図 0-1a. 2-プロパノール (CH3)2CHOH -水 H2O 系の等圧相平衡図。 圧力は 1 atm(= 101.35 kPa)。 図中、水色の線は露点(凝縮)曲線、 青色の線は沸点(沸騰)曲線。 露点曲線と沸点曲線は共沸点 Az で接してそれぞれ極小となります。 共沸点は 353 K で、2-プロパノールのモル分率 \(x_\mrm{Az}\) は 0.69 です。 (DDB data set #24434) | 図 0-1b. 2-プロパノール (CH3)2CHOH -水 H2O 系の等温相平衡図。 図中、水色の線は露点(凝縮)曲線、 青色の線は沸点(沸騰)曲線。 温度は 1 atm での共沸温度の 353.15 K(80 °C)なので、 共沸点での圧力も 1 atm になります。 露点曲線と沸点曲線は共沸点 Az で接してそれぞれ極大となります。 (DDB data set #12230) | 図 0-1c. 2-プロパノール (CH3)2CHOH -水 H2O 系の液体-蒸気の等圧平衡組成図。 圧力 1 atm で温度を変化させた時の、気液平衡状態での 2-プロパノールの液相(\(x\))と気相(\(y\))のモル分率の対応を示します。 共沸点で両者の組成は一致し(\(x_\mrm{Az}=0.69\))、液相が水に富む組成(\(x \lt x_\mrm{Az}\))では気相側に 2-プロパノールが、 液相が 2-プロパノールに富む組成(\(x \gt x_\mrm{Az}\))では水が多く分配されます。 (DDB data set #24434) |
前節で見たのは、混合液体の沸点が純液体の沸点より低くなる、 あるいは混合液体の蒸気圧が純液体の蒸気圧より高くなる共沸現象でしたが、 逆に混合液体の沸点が純液体の沸点より高くなる場合もあります。 こうした成分の組み合わせは比較的まれで、 「負の共沸」と呼ばれます。 図 0-2 に示すのは、負の共沸を示す系としてよく例に出される、 アセトン-クロロホルム系の気液平衡の相図です。
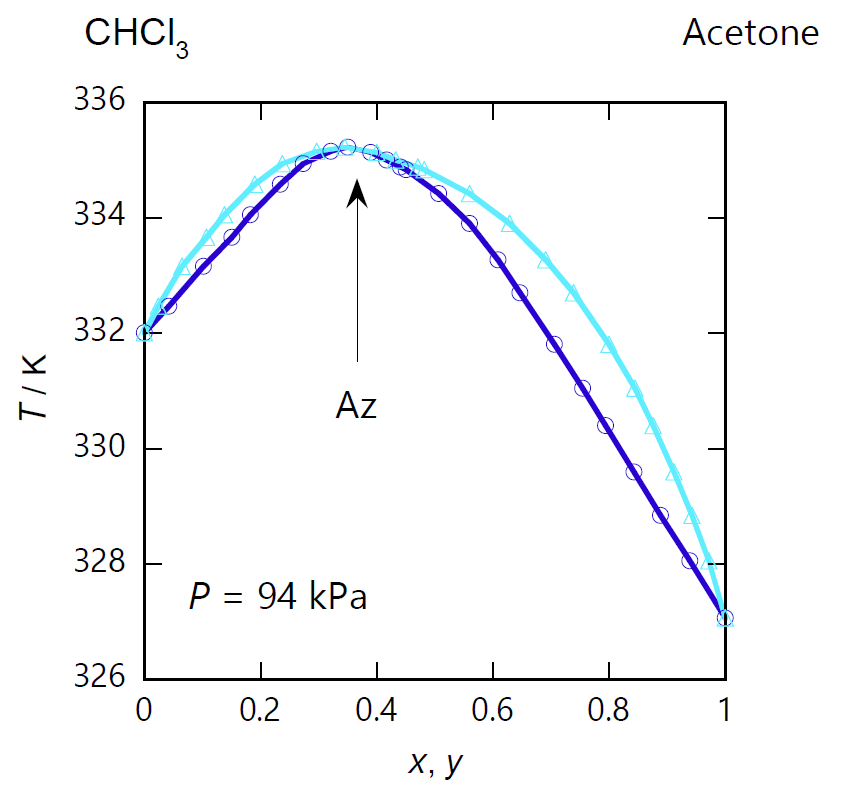
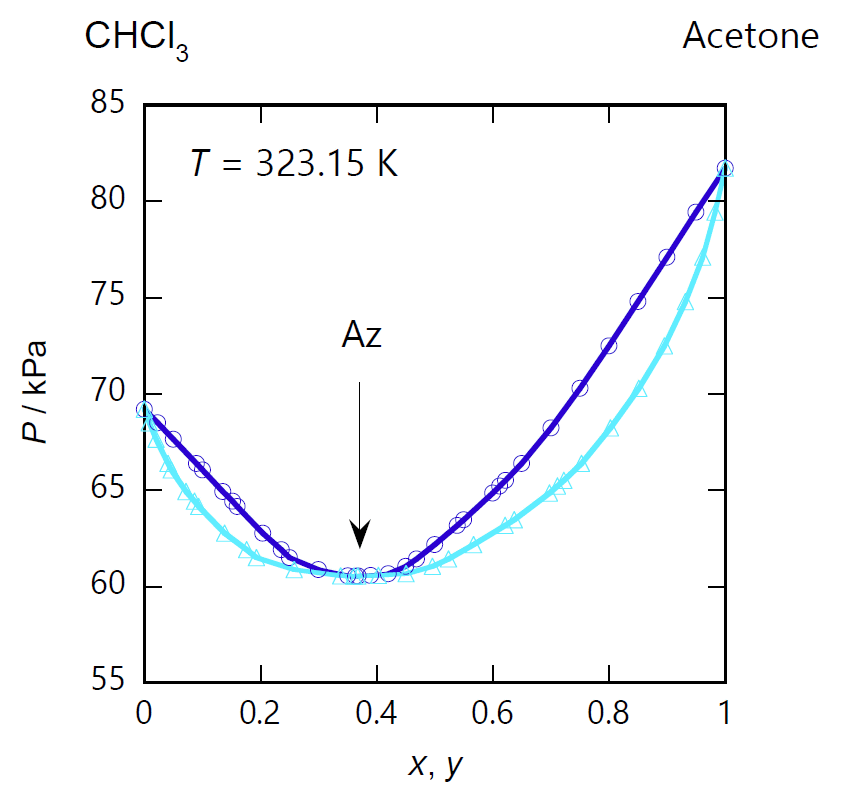
図 0-2a の等圧条件での沸点・露点曲線を見てみると、沸点・露点曲線は共に共沸点で極値を持ちますが、 図 0-1a の 2-プロパノール-水系とは対照的に、 アセトン(標準沸点 56 °C)とクロロホルム(標準沸点 61 °C)を混ぜると、 両者の沸点より高い温度で沸騰・凝縮するようになります (図 0-2a では圧力が 94 kPa と若干 100 kPa より低いので、沸点が 2 °C ほど低くなっています)。 同様に蒸気の凝縮する温度(露点)も高くなります。 図 0-2b の等圧条件での沸点・露点曲線でも 2-プロパノール-水系とは対照的に、 アセトンとクロロホルムを混合すると、 両者の蒸気圧より低い圧力で沸騰・凝縮するようになります。
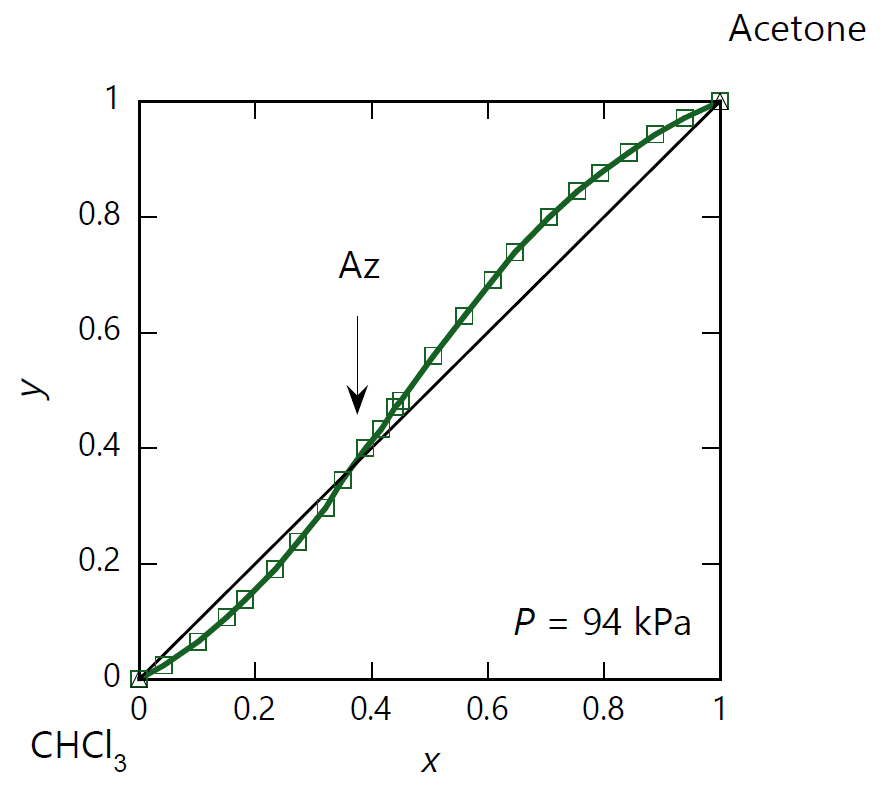
凝縮・沸騰する際の蒸気中のアセトンのモル分率(\(y\))を液相中のモル分率(\(x\))についてプロットしたのが図 0-2c です。 共沸点 \(x=y=0.37\) を境に、液相と気相のアセトンの分配比 \(y/x\) は逆転するのですが、 2-プロパノール-水系とは対照的に、 クロロホルムに富んだ組成ではクロロホルム、アセトンに富んだ組成ではアセトンが、それぞれ気相に多く分配されることになります。 負の共沸を示す系は、いわば ”よそ者” を液相に取り込む傾向のある系、 異種間の相互作用が強い系と考えられるわけです。 アセトン-クロロホルム系の場合には、アセトンとクロロホルムの間の水素結合 (CH3)2C=O…H-CCl3 の存在が挙げられますが、それがただちにモル分率 0.5 での共沸をもたらすわけでないのは、 面白いところです。
|
|
|
| 図 0-2a. アセトン (CH3)2CO -クロロホルム CHCl3 系の等圧相平衡図。 圧力は 94 kPa。 図中、水色の線は露点(凝縮)曲線、 青色の線は沸点(沸騰)曲線。 露点曲線と沸点曲線は共沸点 Az で接してそれぞれ極大となります。 共沸点でのアセトンのモル分率 \(x_\mrm{Az}\) は 0.37 で、共沸温度はほぼ 335 K(62 °C)です。 (DDB data set #24628) | 図 0-2b. アセトン (CH3)2CO -クロロホルム CHCl3 系の等温相平衡図。 図中、水色の線は露点(凝縮)曲線、 青色の線は沸点(沸騰)曲線。 共沸温度は 323.15 K(50 °C)で共沸点の圧力は 60.5 kPa。 共沸組成は 94 kPa の場合より若干小さくなって \(x_\mrm{Az} = 0.36\) です。 (DDB data set #1323) | 図 0-2c. アセトン (CH3)2CO -クロロホルム CHCl3 系の液体-蒸気の等圧平衡組成図。 圧力 94 kPa でのアセトンの液相中(\(x\))と蒸気相中(\(y\))でのモル分率の対応を示します。 共沸点で両者の組成は一致し(\(x_\mrm{Az}=0.37\))、液相がクロロホルムに富む組成(\(x \lt x_\mrm{Az}\))では気相側にクロロホルムが、 液相がアセトンに富む組成(\(x \gt x_\mrm{Az}\))ではアセトンが多く分配されます。 (DDB data set #24628) |
負の共沸を示す液体は、かつてはもっぱら定沸点混合物として知られていました。 今でも定沸点塩酸(あるいは共沸塩酸)として 20 mass% の塩酸が市販されています。 実験室のバッチ式の蒸留で塩酸の蒸留を行うと、 蒸留初期には、共沸組成より濃度の低い塩酸では水に富んだ塩酸が、濃度の高い塩酸では塩化水素に富んだ塩酸が留出し、 留出温度の上昇が止まって一定になったところで(1 気圧では 109 °C)、 最後に共沸組成の塩酸(1 気圧では 20.2 mass%)がフラスコに残ります (正の共沸を示す系も定沸点混合物ではありますが、バッチ式の蒸留を行った場合、 組成の変動に対して安定ではなく、ことさらに定沸点混合物とは呼ばれないようです。 あるいはこの故に共沸 azeotrope という言葉が、 組成の変化しない気液平衡を指す言葉として選ばれたのかもしれません)。 定沸点塩酸は、かつては容量分析の標準物質としても用いられました。 ここでも小学校でも取り上げられる、皆さんおなじみの塩化水素 HCl-水 H2O 系を紹介した方がよかったかもしれませんが、 塩化水素 HCl-水 H2O 系は、さまざまな 2 成分混合液体の中で、 常圧下、おそらくもっとも特異な気液相挙動を示すのでここでは敬遠しておきます (たとえば水に塩化水素はよく溶けますが、液体塩化水素に水はほとんど溶けません)。
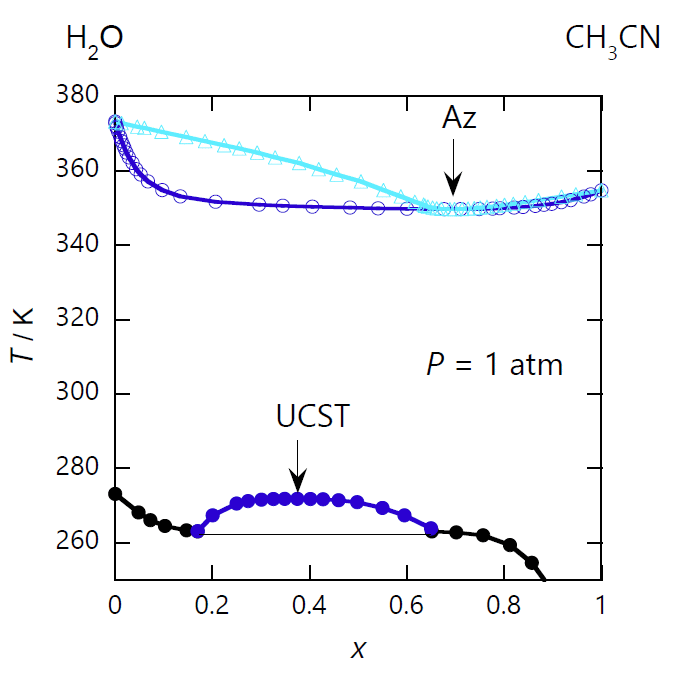
頭の丸い相線は、共沸現象ばかりではなく、 むしろこちらの方がなじみがあるかもしれませんが、臨界現象にともなっても登場します。 最初に紹介したアセトニトリル-水系では、350 K 付近で共沸現象が現れていましたが、 それよりさらに温度を下げると、図 0-3 に見るように -2 °C 以下で液液分離が生じるようになります。 液液分離が生じる最高温度(臨界温度。 しばしば上部臨界溶液温度 Upper Critical Solution Temperature あるいは上部相溶温度 Upper Consolute Temperature と呼ばれます)では、 液液分離の相線は極値を持ち、臨界点で生じてくる 2 液相の組成は等しく、 温度の低下とともに急速に組成差が拡大していきます。 (ここでは温度を下げることで相分離の生じる、上部臨界溶液温度を持つ系を見ましたが、 温度を上げることで相分離の生じるテトラヒドロフラン-水系のような、下部臨界溶液温度を持つ系もあります。)
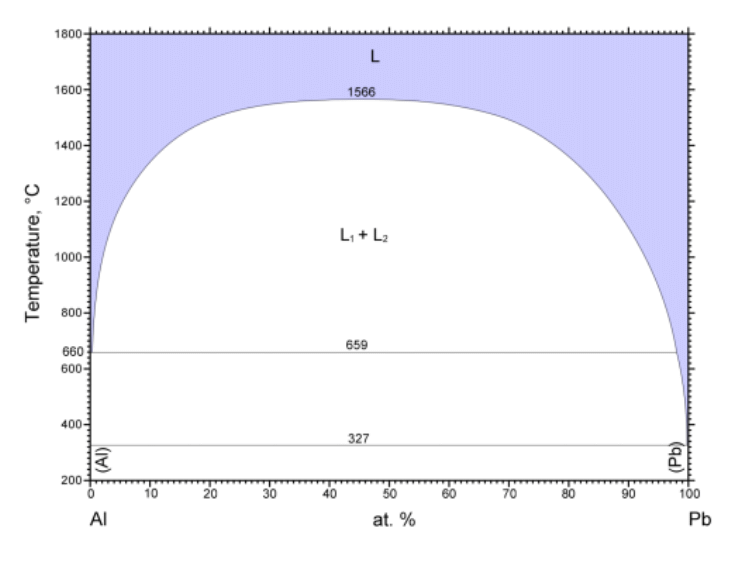
同様の現象は、合金系でもよく知られており、 図 0-4 には、鉛 Pb - アルミニウム Al 系の相図を示しました。 鉛とアルミニウムの液体は、アルミニウムの融点(660 °C)以上でも容易に溶けあいませんが、 温度の上昇とともに相互の溶解度が増し、1566 °C(臨界温度)以上では全組成で溶けあうようになります (臨界点での鉛のモル分率は 0.45(質量分率は 85 mass%)。こうした冶金関連の分野では「上部臨界溶液温度」などとはまず呼ばれません)。
こうした臨界挙動にともなう相線の形状は、 共沸挙動における沸点・露点曲線と似かよっています。 けれども臨界挙動では、あくまで 1 相が 2 相になる(あるいは 2 相が 1 相になる)ことが問題になっていて、 共沸現象のようなある相からある相への転移、あるいは 2 相の共存状態の話とは随分違ってきます。 このため臨界現象についての興味は、 個々の物質の個性ではなく、臨界指数など普遍的な性質 universality に向かうことが多いようです (たとえば温度変化にともなう組成差の拡大の度合いが、臨界指数の β に対応します)。 今回のおはなしでは、組成を同じくする 2 相が共存する場合を取り上げ、 こうした臨界挙動については取り上げません。
|
|
| 図 0-3. アセトニトリル CH3CN -水 H2O 系の等圧相平衡図 (圧力は 1 atm(= 101.35 kPa))。 気液平衡の存在する領域から、さらに温度を下げると、液液分離が生じるようになります。 液液分離の臨界温度(上部臨界溶液温度 UCST)は 272 K、 臨界点でのアセトニトリルのモル分率は 0.37 ぐらいです。 黒い実線は固液の相線でこの温度領域では、氷と液体の共存線です。 (DDB data set #23535, #11025, #6923、) | 図 0-4. 鉛 Pb とアルミニウム Al の相図。 アルミニウムの融点 660 °C では、両者の液体は溶けあいませんが、 温度を 1566 °C まで上げると、すべての組成で溶けあうようになります (共融(共晶)点はそれぞれの純金属の融点と 1 K 程度しか違いません)。 国立研究開発法人物質・材料研究機構 AtomWork http://crystdb.nims.go.jp/ (参照: 2024.3) |
|
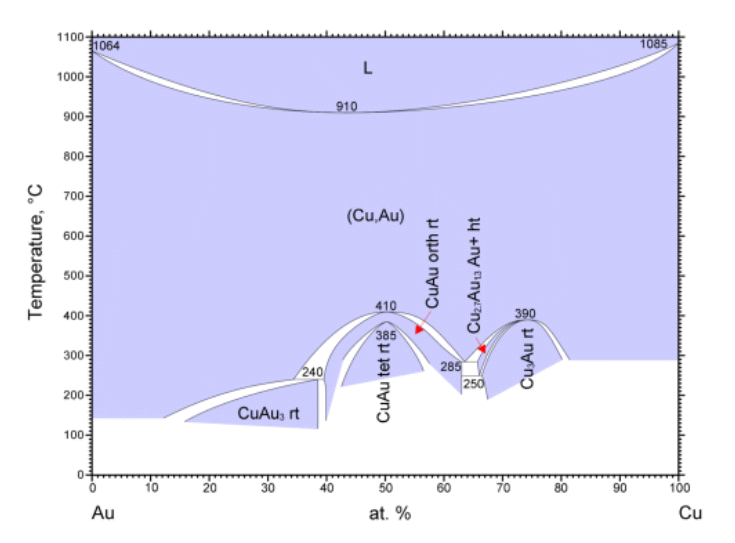
| 図 0-5. 銅 Cu - 金 Au の相図。 国立研究開発法人物質・材料研究機構 AtomWork http://crystdb.nims.go.jp/ (参照: 2024.3) |
合金や水和結晶など、固体の関係する相図にも、 しばしば頭の丸い相線が登場します。 図 0-5 にはこうした例として、古くから知られる銅 Cu -金 Au の相図(状態図)を示しました。 銅と金は固溶体を作り、銅(融点 1085 °C)と金(融点 1064 °C)を混合すると、両者の融点・凝固点より低い温度で融解・凝固するようになります。 融点・凝固点が極小となり、融解・凝固曲線が接するのは 910 °C、銅のモル分率 0.45(銅の質量分率 20 mass%)ぐらいのところです。 この融解・凝固曲線の挙動は、正の共沸現象で見た沸騰・凝縮曲線の挙動と軌を一にしています。 ぼくなどは「共沸」に合わせて「共融」とでもしたいところですが、 こうした挙動は一致融解 congruent melting と呼ばれます (「共融 eutectic」というのは、液相と 2 種の固相の 3 相共存状態について使われます。 なお材料系では「共晶」と呼ぶのが好まれるようです)。
さらに銅 Cu -金 Au の相図には 500 °C 以下の領域で、液相が関与しない、固溶体間の組成の変化しない相転移が現れます。 銅と金の間には、さまざまな金属間化合物が知られており、 相図上で頭の丸い、組成の変わらない転移が見られるのは、CuAu、Cu3Au の組成についてです。 ここで見られる頭の丸い相線の挙動は、 先に見た負の共沸と同様で、 先の一致融解も含めて、一致転移 congruent transition と呼ばれます。 なおここで CuAu(銅の質量分率 24 mass% で、いわゆる 18金相当)については、 410 °C で直方(斜方)晶、385 °C で正方晶への転移が起き、 2段構えの一致転移が見られています。
余談ですが銀 Ag - 金 Au 系では融解・凝固曲線に極値はなく、 また金属間化合物も作らず、全組成で固溶体となります)。
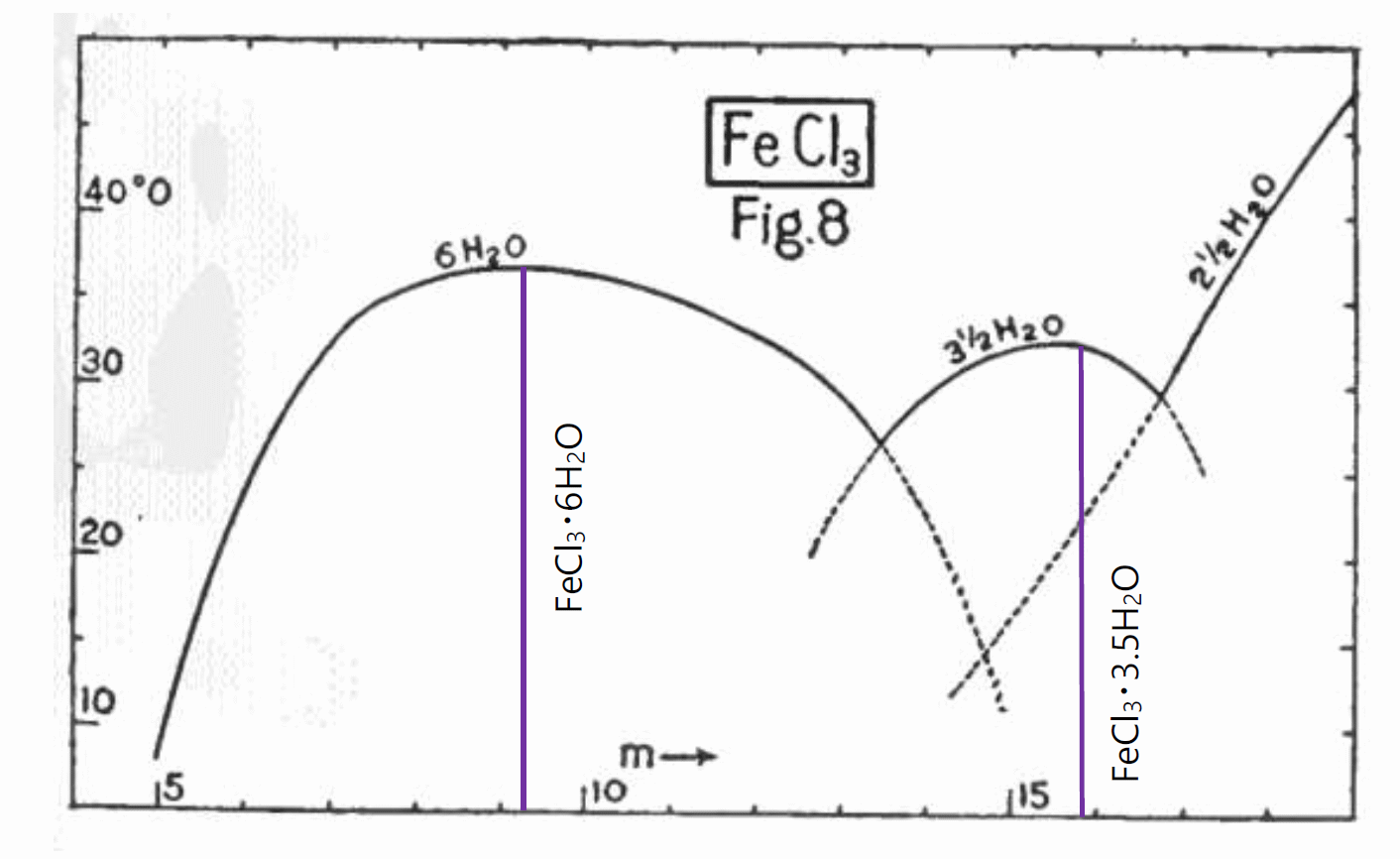
銅 Cu -金 Au 系で 500 °C 以下で見られた負の共沸と同様の一致融解は、 ”化学” のリーグでも水和結晶などで古くからよく知られています。 図 0-6 には、古色蒼然といった International Critical Table に収められた塩化鉄(III) FeCl3 と水の相図を紹介しました。 この塩化鉄(III) FeCl3 の水和塩の溶解挙動の研究は、 大幸先生の「塩類と水」(1913)にも、大きく取り上げられています。 塩化鉄(III) の 6 水和物 FeCl3·6H2O は、37 °C で融解し、 質量モル濃度 9.25 mol/kg の塩化鉄(III) FeCl3 水溶液となります。 よく結晶を得ようと溶液の濃縮操作をしますが、 12 mol/kg の濃厚な塩化鉄(III)溶液では、35 °C 付近で濃縮しても 6 水和物の結晶は出てこず、 逆に水を加えて薄めることで 6 水和物 FeCl3·6H2O の結晶が得られるわけです。
この相図が負の共沸や銅-金系の金属間化合物の相図と異なっているのは、 塩化鉄(III) の水和物の固相の存在する組成の幅が極めて小さいとされ、 固溶体の存在が無視されていることです。 組成の変化は不純物あるいは格子欠陥として認識され、相図上に居場所がなくなっているのです。 たいていの場合、溶液と平衡状態にある水和結晶の中に溶け込む水、あるいは失われる水の量は微々たるもので、 相図上にプロットしたとしても、ほぼ一本の線になってしまうわけです。
そうした時でも、液相側は組成の大きな変動を許容し、 ギブズ-コノバロフの法則の主張するように、 2 相が平衡に存在する場合、共存温度に極値を示します。 この点、図 0-6 で若干、塩化鉄(III) の 3.5 水和物 FeCl3·3.5H2O の溶解の相線の極値が、 FeCl3·3.5H2O の組成(FeCl3 の質量モル濃度 15.9 mol/kg)より、 若干低めに描かれているのは法則に反していて問題です (Roozeboom の元の論文では、 極大になることになっています)。
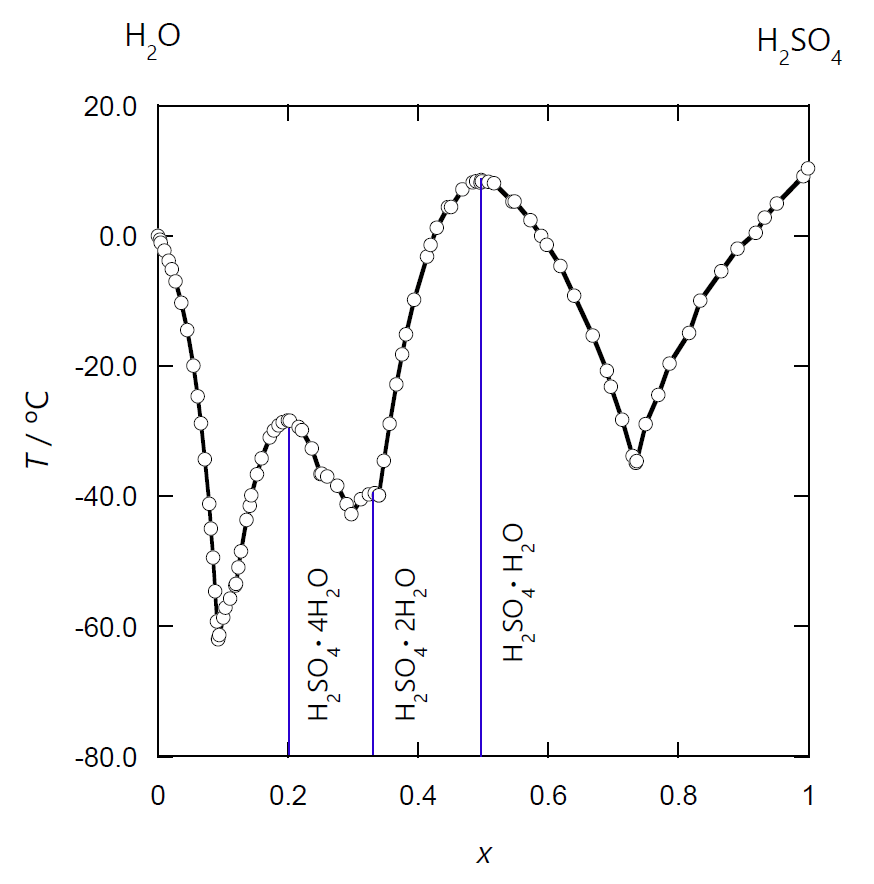
図 0-7 には、硫酸 H2SO4 -水 H2O 系の固液の相図を示しました (ここには触れませんが、硫酸-水の気液の相図にも、負の共沸現象が現れます)。 硫酸に水和塩の内、4、2、1 水和物について、一致融解が見られます。 また硫酸 H2SO4 は三酸化イオウ SO3 の水溶液なわけですが、 発煙硫酸のように、硫酸より高濃度の三酸化イオウ溶液が存在します。 そして硫酸自身も一致融解を示し、融点が極値を示します(二硫酸 H2S2O7 の固相も得られ、 その一致転移も知られています)。
|
|
| 図 0-6. 塩化鉄(III) FeCl3 の水への溶解挙動。 縦軸は温度、横軸は塩化鉄(III) FeCl3 の質量モル濃度。 FeCl3·6H2O の融液は FeCl3 の質量モル濃度 9.25 mol/kg、 FeCl3·3.5H2O の融液は質量モル濃度 15.9 mol/kg に相当します。 International Critical Table Vol. 4 (1926) より。 | 図 0-7. 硫酸 H2SO4 -水 H2O 系の固液の相図(準安定な相線は省略)。 硫酸には種々の水和結晶が知られていますが、 6 水和物 H2SO4·6H2O と 3 水和物 H2SO4·3H2O については、 対応する液相の領域が、他の水和結晶の領域に覆われて、一致融解が見られません。 また図からは明瞭ではありませんが、硫酸 H2SO4 自身も一致融解を示し、 融点が極値を示します。 三酸化イオウ SO3 - 水 系の相図から作成。 |