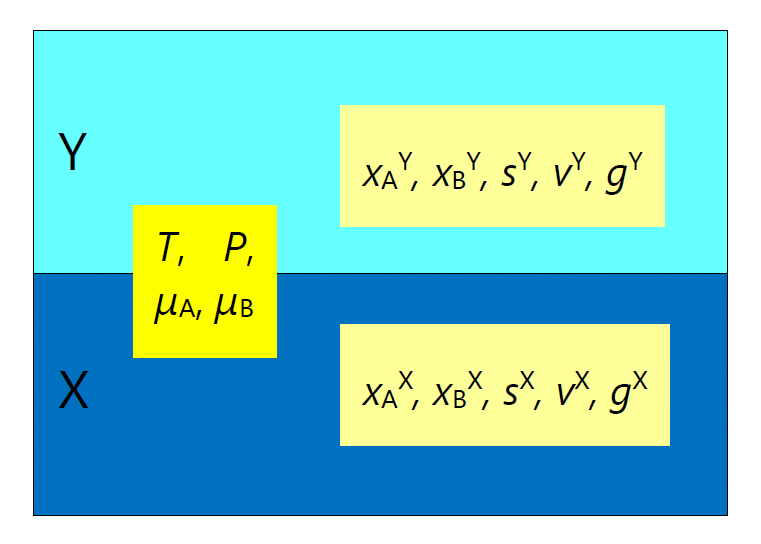
2種の成分 A、B の物質量をそれぞれ \(n_\mrm{A}\)、\(n_\mrm{B}\) 含む、 体積 \(V\) の2成分混合系を考えます。 この系で、2つの相 X と Y が平衡に存在する時、 それぞれの相の熱力学的な状態を特徴づける示強的な変数は大きく2種類に分けることができます。
一方は密度や組成などの X、Y それぞれの相を特徴づけるもので、 物質量 \(n\) やエントロピー \(S\) 、ギブズエネルギー \(G\) といった示量的な量を、 一方の示量的な量との比、単位体積当たりや単位物質量当たりの形で表したものです。 ここではよく使われる、単位物質量当たりの量、モル体積 \(v\)、モルエントロピー \(s\)、 モルギブズエネルギー \(g\) をもっぱら使用します。 また単位物質量当たりの A、B の物質量はモル分率 \(x\) です。
\begin{eqnarray} v &=& V/(n_\mrm{A} + n_\mrm{B}) , ~~~~s = S/(n_\mrm{A} + n_\mrm{B}), ~~~~g = G/(n_\mrm{A} + n_\mrm{B}), \nonumber \\ x_\mrm{A} &=& n_\mrm{A}/(n_\mrm{A} + n_\mrm{B}) ,~~ x_\mrm{B} = n_\mrm{B}/(n_\mrm{A} + n_\mrm{B}) \label{eq:vsx} \end{eqnarray}
単位物質量当たりの量で考えるというのは、 全物質量 \(n_\mrm{A} + n_\mrm{B} = \mrm{const} = 1\) という拘束条件のもとで考えるのと同じことです。 ですからモル分率 \(x_\mrm{A}\) についての量 \(q = Q/(n_\mrm{A} + n_\mrm{B}) = Q\) の微分は、 \((n_\mrm{A}, n_\mrm{B})\) という変数の組を取った場合と次の関係にあります (ここで \({\rmd}/{\rmd x_\mrm{A}}\) は、\(n_\mrm{A} + n_\mrm{B} = 1\) での微分です): \[ \frac{\rmd q}{\rmd x_\mrm{A}} = \pdifA{Q}{n_\mrm{A}}{n_\mrm{B}} \frac{\rmd n_\mrm{A}}{\rmd x_\mrm{A}} + \pdifA{Q}{n_\mrm{B}}{n_\mrm{A}}\frac{\rmd n_\mrm{B}}{\rmd x_\mrm{A}} = \pdifA{Q}{n_\mrm{A}}{n_\mrm{B}} - \pdifA{Q}{n_\mrm{B}}{n_\mrm{A}} \] あとで問題にしますが、モルギブズエネルギーについては、次の関係が成立します: \[ \pdifA{g}{x_\mrm{A}}{T,P} = \pdifA{G}{n_\mrm{A}}{T,P,n_\mrm{B}} - \pdifA{G}{n_\mrm{B}}{T,P,n_\mrm{A}} = \mu_\mrm{A} - \mu_\mrm{B} \] 少し話が飛躍しすぎるかもしれませんが、仮想的な化学反応 B → A で、反応進行度 \(x_\mrm{A}\) における、 反応にともなう \(Q\) の変化 \(\Delta Q_\mrm{r} = Q_\mrm{A} - Q_\mrm{B}\) を考えるようなものだといってもいいでしょう。
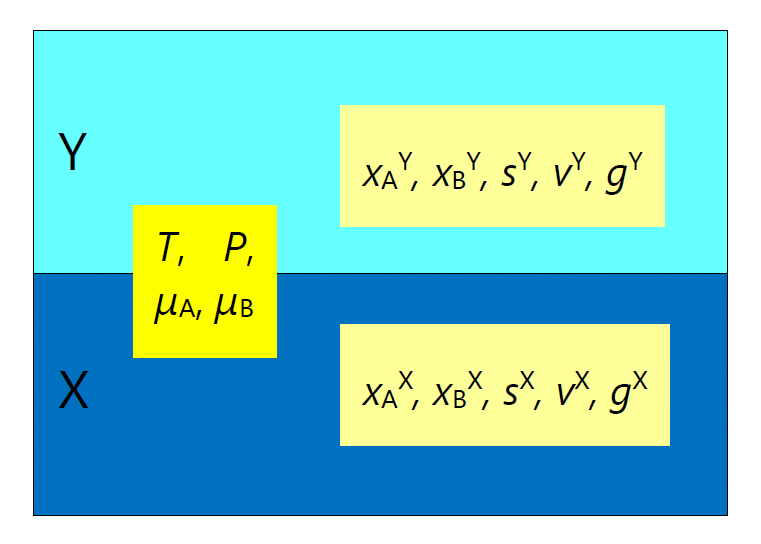
|
| 図 1-1. X、Y 2相が平衡にある時の示強変数の組み合わせ。 モル分率やモル体積といった「密度」は、相によって一般に異なりますが、 温度や圧力といった「ポテンシャル」は等しくなります。 |
一方温度 \(T\)、圧力 \(P\)、各成分の化学ポテンシャル \(\mu_\mrm{A}\)、 \(\mu_\mrm{B}\) は、 両相で等しくなっていないといけません:
\begin{eqnarray} T &=& T^\mrm{X} &=& T^\mrm{Y}, ~~P &=& P^\mrm{X} &=& P^\mrm{Y}, \nonumber \\ \mu_\mrm{A} &=& \mu_\mrm{A}^\mrm{X} &=& \mu_\mrm{A}^\mrm{Y}, ~~ \mu_\mrm{B} &=& \mu_\mrm{B}^\mrm{X} &=& \mu_\mrm{B}^\mrm{Y} \label{eq:TPmu} \end{eqnarray}
こうした示強的変数を、ここでは「ポテンシャル」と呼び、 先のモル体積やモル分率などは、カッコつきの「密度」と呼ぶことにします。
均一相で成り立つ次のギブズ-デュエムの関係は、この「ポテンシャル」と「密度」、 2種の示強的変数の相互の立ち位置を示してくれているといえるでしょう:
\begin{equation} s \rmd T - v \rmd P + x_\mrm{A} \rmd \mu_\mrm{A} + x_\mrm{B} \rmd \mu_\mrm{B} = 0 \label{eq:GDp} \end{equation}
興味深いのは、「密度」が「ポテンシャル」の間の偏微分の形で与えられることです。 この点、式 \eqref{eq:GDp} を \(x_\mrm{A} + x_\mrm{B} = 1\) に注意して次のように書き直すと、 見通しが良くなります。 成分 A を基準にして、それとの差 \(\mu_\mrm{B} - \mu_\mrm{A}\) で系を記述しようというわけです:
\begin{equation} \rmd \mu_\mrm{A} = -s \rmd T + v \rmd P - x_\mrm{B} \rmd (\mu_\mrm{B} - \mu_\mrm{A}) \label{eq:GDq} \end{equation}
たとえばモル体積は次式で与えられます:
\begin{equation} v = \pdifA{\mu_\mrm{A}}{P}{T,\mu_\mrm{B} - \mu_\mrm{A}} \label{eq:molv} \end{equation}
またギブズ-デュエムの関係は、均一相中、2成分系で独立に振舞う「ポテンシャル」が 3 個であることを示しています。 ギブズの相律で、自由度 \(F\)、成分の数 \(C\)、相の数 \(\phi\) の間の関係
\begin{equation} F = C - \phi + 2 \label{eq:phaserule} \end{equation}
でいうと、\(C = 2\)、\(\phi = 1\) の場合に対応しています。
X、Y 2相が平衡状態で共存している状態では、式 \eqref{eq:TPmu} にみるように、両相の「ポテンシャル」は等しく、 ギブズ-デュエムの関係、式 \eqref{eq:GDq} から、それぞれの相について次の式が成り立ちます:
\begin{eqnarray} \rmd \mu_\mrm{A} = -s^\mrm{X} \rmd T + v^\mrm{X} \rmd P - x_\mrm{B}^\mrm{X} \rmd (\mu_\mrm{B} - \mu_\mrm{A}) \nonumber \\ \rmd \mu_\mrm{A} = -s^\mrm{Y} \rmd T + v^\mrm{Y} \rmd P - x_\mrm{B}^\mrm{Y} \rmd (\mu_\mrm{B} - \mu_\mrm{A}) \label{eq:GibbsDuhem} \end{eqnarray}
ですから X、Y 2相の「密度」\(q\) の差を次のように表記すると
\begin{equation} \Delta q = q^\mrm{Y} - q^\mrm{X} \label{eq:deltaq} \end{equation}
2相共存状態で次式が成り立ちます:
\begin{equation} \Delta s \rmd T - \Delta v \rmd P + \Delta x_\mrm{B} \rmd (\mu_\mrm{B} - \mu_\mrm{A}) = 0 \label{eq:GibbsDuhemx} \end{equation}
この状態では系の自由度は \(C - \phi + 2 = 2\) です。 さて2相の組成が同じ状態(\(\Delta x_\mrm{A} = -\Delta x_\mrm{B} = 0\))で2相が共存しているなら次式が成立します(自由度 1):
\begin{equation} \Delta s \rmd T - \Delta v \rmd P = 0 \label{eq:GibbsKol} \end{equation}
この式は1成分系における、クラペイロン-クラウジウスの式に相当すると見ることができます:
\begin{equation} \pdifA{P}{T}{x_\mrm{A}^\mrm{Y}=x_\mrm{A}^\mrm{X}, \Delta \mu_\mrm{A}} = \frac{\Delta s}{\Delta v} \label{eq:2conCCeq} \end{equation}
1 成分系であればこれで話は閉じるわけですが、 2 成分系では組成の変動についての考慮が必要です。 式 \eqref{eq:GibbsKol} は \(\Delta x_\mrm{A} = 0\) の条件の下では、 圧力一定(\(\rmd P = 0\))であれば、組成の変動、化学ポテンシャルの変動に対して、 2 相の共存温度の変動がないこと(\(\rmd T = 0\))、 温度が極値を示すことを意味します(相線の頭が丸い)。 つまり前節で見たように、温度 \(T\) - 組成 \(x\) の等圧相平衡図で、沸点、露点曲線は、いずれも共沸点で極値を持つわけです。 同様に温度一定(\(\rmd T = 0\))であれば圧力の変動がないわけで(\(\rmd P = 0\))、 組成に対し圧力が極値を示すことに対応します。 これがギブズ-コノバロフの法則(定理あるいは規則)と呼ばれるものになります。
\(\Delta x_\mrm{A} = 0\) の条件で、 共存温度(あるいは共存圧力)が極値を示すのであれば、 ほぼ純粋な B、\(x_\mrm{A} \simeq 0\)(あるいはほぼ純粋な A、\(x_\mrm{A} \simeq 1\)) でも \(\Delta x_\mrm{A} \simeq 0\) で、相線が極値を持つようにも思えます。 しかし A の濃度を 0 に近づけていくと、A の化学ポテンシャルはいくらでも小さくなり(\(\rmd \mu_\mrm{A} \propto x_\mrm{A}^{-1}\))、 式 \eqref{eq:GibbsDuhemx} の左辺第 3 項は 0 になりません。 それで式 \eqref{eq:GibbsKol} は成り立たず、 \(x_\mrm{A} = 0\)(あるいは \(x_\mrm{A} = 1\))で共存温度、圧力は極値を示しません。 次節の式 \eqref{eq:TxCoexx} も参照ください。
ギブズは、こうした議論から2相の組成が一致する時、 極値が現れることを指摘しました。 一方コノバロフは、水-アルコール(C1 ~ C4)系、 水-カルボン酸(C1 ~ C4)系について蒸気圧の測定を行い、 実験的に蒸気圧曲線に極大(水-プロパノール系)、極小(水-ギ酸系)が現れることを明らかにしました。 なおコノバロフの時代、実験する上でちょっと今では考えられない苦労があったようです。 たとえばメタノールの市販品の純度が低かったためか、一端シュウ酸エステルにして水酸化カルシウムで加水分解。 それを精留してメタノールを得るという手順を踏んでいます。 今は試薬メーカーが JIS などで標準化された種々の試薬を供給する体制が整えられていて、 本当に便利になったものです。
前節では平衡に共存する2相で組成が同じであれば、圧力一定であれば共存温度が、温度一定であれば共存圧力が、 組成に対し極値を取ることを見ました。 でもこれだけでは、極大か極小か、正の共沸か負の共沸かは判断できません。 ここではもう少し詳しく、 共沸点近傍の挙動を調べてみることにしましょう。
先のギブズ-デュエムの関係から得られる、相共存状態での関係式 \eqref{eq:GibbsDuhemx} から、 圧力一定の条件下、X 相中の A のモル分率 \(x_\mrm{A}^\mrm{X}\) に対する、平衡温度の依存性を見てみましょう。 このためには \((T, P, \mu_\mrm{B}-\mu_\mrm{A})\) という変数の組を、\((T, P, x_\mrm{A}^\mrm{X})\) に取り替えます。 共沸点近傍では、平衡温度、圧力の組成依存性は小さいので、 式 \eqref{eq:GibbsDuhemx} から次式が得られます:
\begin{equation} \Delta s \rmd T \simeq \Delta x_\mrm{A} \pdifA{(\mu_\mrm{B} - \mu_\mrm{A})}{x_\mrm{A}^\mrm{X}}{T,P} \rmd x_\mrm{A}^\mrm{X} \label{eq:TxCoexx} \end{equation}
ここでモル分率についての微分が出てきますが、 そもそもモルギブズ自由エネルギー \(g\) の \(T, P\) 一定でのモル分率 \(x_\mrm{A}\) についての微分が \(\mu_\mrm{A} - \mu_\mrm{B}\) であることに注意すると次式が得られます:
\begin{equation} \pdifA{(\mu_\mrm{B} - \mu_\mrm{A})}{x_\mrm{A}^\mrm{X}}{T,P} = - \left( \frac{\partial^2 g}{\partial x_\mrm{A}^2} \right)_{T,P}^\mrm{X} = - \left( \frac{\partial^2 g}{\partial x_\mrm{B}^2} \right)_{T,P}^\mrm{X} = -g_{xx}^\mrm{X} \label{eq:gxx} \end{equation}
ここでモルギブズエネルギー \(g\) の、A(あるいは B)のモル分率についての、 温度・圧力一定での 2 階微分を \(g_{xx}\) としました。 平衡状態においてモルギブズエネルギーは、温度・圧力一定の条件下、 最小値を取ります。 ですから局所的に考えた時、相が安定であるためには、組成、モル分率の変化に対して、 モルギブズエネルギーは下に凸でないといけません (物質的安定性あるいは拡散安定性。もし上に凸であれば、 組成の変動に対して系が安定化することになり、 組成の変動が自発的に拡大していきます)。 つまり \(g_{xx}\) は正である必要があります:
\begin{equation} g_{xx}^\mrm{X} \gt 0 \label{eq:stable} \end{equation}
式 \eqref{eq:TxCoexx} の左辺 \(\Delta s \rmd T\) の項は、詳しく書けば次のようになるところです: \[ \left[ \Delta s + \Delta x_\mrm{A} \pdifA{(\mu_\mrm{B} - \mu_\mrm{A})}{T}{P, x_\mrm{A}^\mrm{X}} \right] \rmd T = [\Delta s - \Delta x_\mrm{A} (S_\mrm{B}^\mrm{X} - S_\mrm{A}^\mrm{X})] \rmd T = [x_\mrm{A}^\mrm{Y} \Delta S_\mrm{A} + x_\mrm{B}^\mrm{Y} \Delta S_\mrm{B}] \rmd T \] ここで \(S_\mrm{A}\)、\(S_\mrm{B}\) は、それぞれ成分 A、B の部分モルエントロピーです。 共沸点付近では \(\Delta x_\mrm{A} \sim 0\) なので、式 \eqref{eq:TxCoexx} のように簡単化しているわけです (\(s = x_\mrm{A} S_\mrm{A} + x_\mrm{B} S_\mrm{B}\) であることに注意)。
式 \eqref{eq:TxCoexx} を書き換えると、次式が得られます:
\begin{equation} \pdifA{T}{x_\mrm{A}^\mrm{X}}{P, \Delta \mu_\mrm{A}=0} \simeq - \frac{\Delta x_\mrm{A}}{\Delta s} g_{xx}^\mrm{X} \label{eq:TxCoexLine} \end{equation}
また Y 相の組成についても同様の関係が成り立ち、 X 相と Y 相の組成の間には次の関係があります:
\begin{equation} \pdifA{x_\mrm{A}^\mrm{Y}}{x_\mrm{A}^\mrm{X}}{P, \Delta \mu_\mrm{A}=0} \simeq \frac{g_{xx}^\mrm{X}}{g_{xx}^\mrm{Y}} \gt 0 \label{eq:xyCoexLine} \end{equation}
共沸点で、X、Y 2相の相線は接して、共存温度は極値を取ります。 そして共存温度が共沸温度から少し外れた時、その組成は共沸組成から同じ方向にずれる。 つまり X の相線が極大なら Y の相線も極大、X の相線が極小なら Y の相線も極小というわけです。
ここまで、相の共存温度の等圧条件での組成依存性を見ましたが、 等温条件での圧力の組成依存性についても、同様に関係式を導くことができます。 式 \eqref{eq:GibbsDuhemx} は、等温条件では式 \eqref{eq:gxx} に注意して次のようになり、
\begin{equation} \Delta v \rmd P \simeq \Delta x_\mrm{A} g_{xx}^\mrm{X} \rmd x_\mrm{A}^\mrm{X} \label{eq:PxCoexx} \end{equation}
等温条件での圧力の組成依存性について、次式が得られます:
\begin{equation} \pdifA{P}{x_\mrm{A}^\mrm{X}}{T, \Delta \mu_\mrm{A}=0} \simeq \frac{\Delta x_\mrm{A}}{\Delta v} g_{xx}^\mrm{X} \label{eq:PxCoexLine} \end{equation}
式 \eqref{eq:TxCoexLine} そして式 \eqref{eq:PxCoexLine} から、先にギブズ-デュエムの関係で見たように、 相共存温度及び圧力が両相の組成の一致する点 \(\Delta x_\mrm{A} = 0\) で極値を持つであろうことはわかりますが、 もう少し踏み込んで、極大か、極小かを決める要因を見ておきましょう。 共沸点での相線の 2 階微分を見てみると、次のようになります:
\begin{equation} \left( \frac{\partial^2 T}{\partial (x_\mrm{A}^\mrm{X})^2} \right)_{P, \Delta \mu_\mrm{A}=0} = -\pdifA{\Delta x_\mrm{A}}{x_\mrm{A}^\mrm{X}}{P, \Delta \mu_\mrm{A}=0} \frac{g_{xx}^\mrm{X}}{\Delta s} = (g_{xx}^\mrm{Y} - g_{xx}^\mrm{X}) \frac{g_{xx}^\mrm{X}}{\Delta s g_{xx}^\mrm{Y}} = \frac{\Delta g_{xx}}{\Delta s} \frac{g_{xx}^\mrm{X}}{g_{xx}^\mrm{Y}} \label{eq:TxCoexLine2nd} \end{equation}
同様に共存圧力については次式が成り立ちます:
\begin{equation} \left( \frac{\partial^2 P}{\partial (x_\mrm{A}^\mrm{X})^2} \right)_{T, \Delta \mu_\mrm{A}=0} = -(g_{xx}^\mrm{Y} - g_{xx}^\mrm{X}) \frac{g_{xx}^\mrm{X}}{\Delta v g_{xx}^\mrm{Y}} = -\frac{\Delta g_{xx}}{\Delta v} \frac{g_{xx}^\mrm{X}}{g_{xx}^\mrm{Y}} \label{eq:PxCoexLine2nd} \end{equation}
蒸発、凝縮に引き付けて、X を液体 liq、Y を蒸気 vap とすれば、 蒸発のエントロピー変化 \(\Delta s\)、体積変化 \(\Delta v\) は一般に正です。 ですから等圧条件で温度が極小になる時(正の共沸)、等温条件で圧力が極大になり、 逆に温度が極大になる時(正の共沸)、圧力が極小になります。 また正の共沸の場合には液体のモル自由エネルギーの曲率が、蒸気のモル自由エネルギーの曲率より小さく、 負の共沸の場合には逆になります:
\begin{equation} g_{xx}^\mrm{vap} \gt g_{xx}^\mrm{liq} \gt 0 ~~~~ \mbox{正の共沸} \label{eq:PosAze} \end{equation}
\begin{equation} g_{xx}^\mrm{liq} \gt g_{xx}^\mrm{vap} \gt 0 ~~~~ \mbox{負の共沸} \label{eq:NegAze} \end{equation}
|
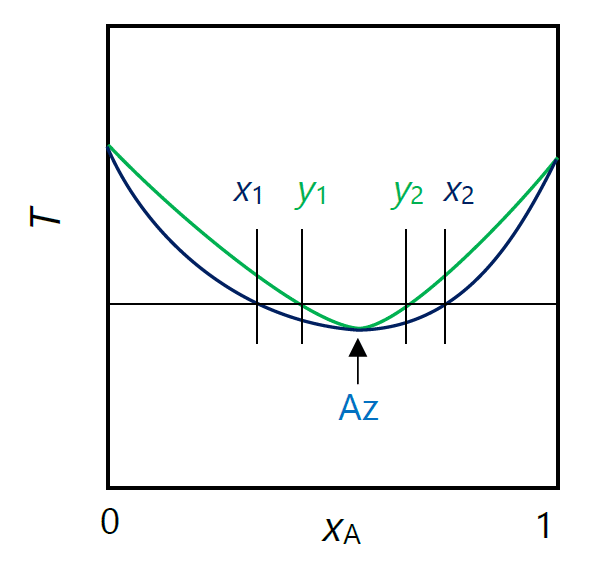
| 図 2-1. 正の共沸現象の \(Tx\) 図。 |
ここまで共沸現象に関わって、熱力学関係式の導出をしてきたわけですが、 図 2-1 に示すような、典型的な正の共沸現象について、 モルギブズエネルギーのグラフ上での挙動を見てみることにしましょう (すでにギブズは同様の解釈を行っています)。
A、B 2 成分系で温度 \(T\)・圧力 \(P\) が定まれば、 2相共存状態での系の自由度は 1 で、 組成、モル分率 \(x_\mrm{A}\) を決めれば、他の「密度」も決まります。 「密度」の中でも特にモルギブズエネルギー \(g\) は、温度、圧力一定の条件下で、 平衡状態で最小値を取るので議論の見通しがよく、 (通常の実験で制御可能な条件との対応がよいこともあって、) 相平衡の議論ではもっぱら採用されていておなじみでしょう。
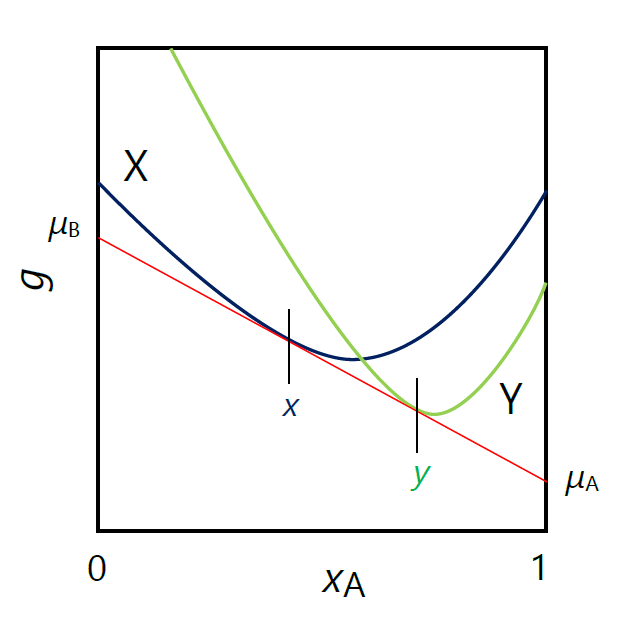
まずモルギブズエネルギーから見た、気液平衡の議論を復習しておきましょう。 図 2-2a に、温度、圧力一定の条件で、 組成を変化させた時の X 相(液体とします)、Y 相(蒸気とします)のモルエネルギー変化を示しました。 最初純粋な B からなる状態(\(x_\mrm{A} =0\))では、 液体のモルギブズエネルギー(\(g^\mrm{X}\))の方が、気体のモルギブズエネルギー(\(g^\mrm{Y}\))より小さく、 液体(X)で存在します。 逆に純粋な A からなる状態(\(x_\mrm{A} =1\))では、(\(g^\mrm{X} \gt g^\mrm{Y}\))で、 蒸気(Y)です。 純粋な B に A を加えていくと、液体から蒸気に相変化するわけですが、 中間に両相が共存する状態、気液共存状態を経ることになります。 共存する両相の組成は、X 相とY 相のモルギブズエネルギー曲線の共通接点(図中、モル分率 \(x\) と \(y\) の点)で与えられます。 この中間のモル分率 \(x \lt x_\mrm{A} \lt y\) では、モル分率 \(x\) の液体と \(y\) の蒸気に相分離します。 また共通接線の勾配は \(-(\mu_\mrm{B} - \mu_\mrm{A})\) であり、2 相共存状態での A、B の化学ポテンシャルは、\(x_\mrm{A} =1\) 、\(x_\mrm{A} =0\) での切片で与えられます。
正の共沸現象の起きる場合、 純粋な A、B からなる状態(\(x_\mrm{A} =0\))では、 液体のモルギブズエネルギー(\(g^\mrm{X}\))の方が、蒸気のモルギブズエネルギー(\(g^\mrm{Y}\))より小さく、 液体(X)で存在します。 そして両者を混合すると、 図 2-2b のように蒸気(Y)のモルギブズエネルギー曲線が液体(X)のモルギブズエネルギー曲線を突き抜けて、 気相の方が安定な組成領域が出現するようになります。 温度を変え、この2つのモルギブズエネルギー曲線がちょうど接した時が共沸点に相当するわけです。
こうしたことが起きるためには、 気相(Y)のモルギブズエネルギー曲線の曲率が、 液相(X)より大きくないといけません (式 \eqref{eq:PosAze})。 また共沸点がモルギブズエネルギー曲線同士の接点ですから、 両相の組成が一致することになります。
|

|
| 図 2-2a. A、B 2 成分の X、Y2相共存時におけるモルギブズエネルギー \(g\) の組成(モル分率 \(x_\mrm{A}\))依存性。 | 図 2-2b. 図 2-1 の共沸現象を示す場合の、A、B 2 成分のモルギブズエネルギー \(g\) のモル分率 \(x_\mrm{A}\) 依存性。 |