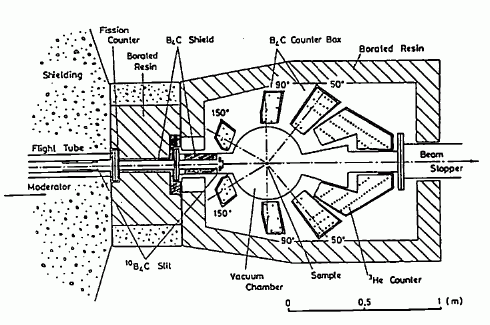
図 9. 中性子線回折装置(高エネルギー研究所、HIT)

原理的な話はこれぐらいにして、実際の中性子線を用いた装置の例を示しましょう。 図 9 は、高エネルギー物理学研究所にあるパルス中性子源(KENS)に設置されている S(Q) の測定装置(HIT)です。 この装置では、角度を動かすのではなく、もっぱら中性子線の波長(エネルギー)を変えることによって Q を変えています。 こうした測定手法をエネルギー分散型といいます。角度ではなく波長を変えることのメリットとしては、 複雑な構成の試料容器あるいは試料周辺機器を使う際に、空きスペースを有効に使えること、そして広い Q 領域の S(Q) の測定が可能で、 高分解能の動径分布関数が得られることが挙げられます。 この一方、波長を変えるとともに、入射中性子線の強度が変ることを考慮に入れないといけない分だけ、 角度変化させる方法より、強度の規格化に難点が残ります。
(22)式で考えたのは、1種類の原子核からなる、分子内の構造のない系での話でした。 しかしたいていの液体では、分子は構造を持ち、何種類かの原子からなっています。 こうした分子性液体の場合には、観測される構造因子は、 各原子核間の配置の情報をそれぞれの散乱長の重みを掛けて足し込んだものになります (たとえばベンゼンで、C-C 距離に注目した分布関数と、 H-H 距離に注目した分布関数は異なることに注意してください)。 そしてさらに、そこには分子内と分子間の構造が折り込まれているのです。 したがって、構造因子と液体構造の間には、(22)式のような簡単な関係は成り立ちません。 分子性液体の構造因子の解析には、異なる原子核の間の分布を考慮するとともに、 (16)式で見たような2原子分子での取り扱いと、 (22)式の単純液体の取り扱いを、組合わせたような方法が必要になってきます。
このように分子性液体の構造解析には難しい問題があるので、 単純液体に比べて研究はあまり進んでいません。 中でも、液相から気相までの幅広い密度領域で、分子性液体の構造がどう変化していくかは、 液体を理解する上で根本的な問題であり、興味のもたれるところですが、 まだ十分に検討されていません。 そうした数少ない検討例として、四塩化炭素についてお話ししましょう。
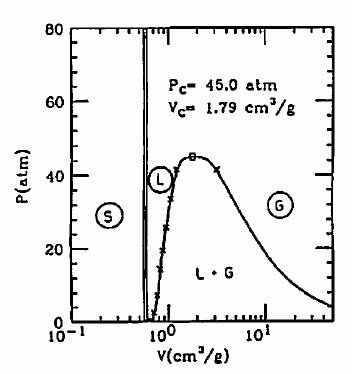
図 10. 四塩化炭素の相図。図中×は実験した点を示す。 |
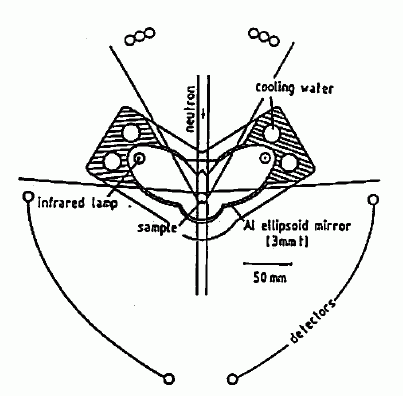
図 11. 試料セルの構成。 |
実験では、常圧で試料を密封した容器を加熱することによって、 気液共存線上での S(Q) の挙動を調べました。 容器中の試料の充填量を適当に選ぶと、1本の密封試料で、 温度のコントロールのみにより、いろんな密度での実験が可能になります。 この実験は図 10 の相図の中の×印の点で行いました。 容器には、180℃以下ではチタン-ジルコニウム合金製のセルを、 180℃以上では石英セルを用いています。 図 11 のように筒状の容器を、アルミニウム製の楕円形の鏡の焦点に置いて、 もう一方の焦点の位置に置いた赤外線ランプで、容器を加熱します。 こうした時、先ほども触れましたように、角度を変えるより波長を変える装置の方が、 いろいろものを組込めて便利です。
チタン-ジルコニウム合金を用いたのは、チタンが散乱長が負、 ジルコニウムが正で互いに打ち消しあい、容器からの回折線がほとんどなくなるからです。 ですから中性子回折の実験では重宝な材料なのですが、今回の場合、 180℃以上にすると、四塩化炭素とチタン-ジルコニウム合金との化学反応が起きることがわかりました。 それで180℃以上では、石英セルを用いています。
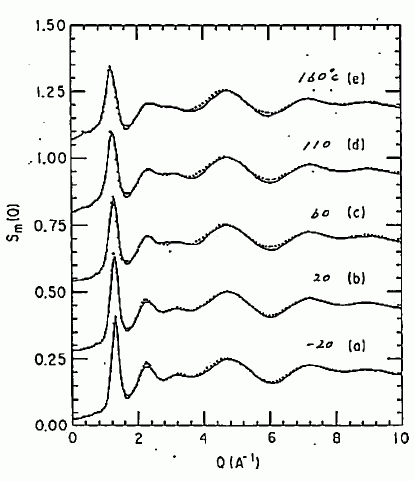
図 12. 四塩化炭素の構造因子。図中、・は実験値、実線は計算値。 |
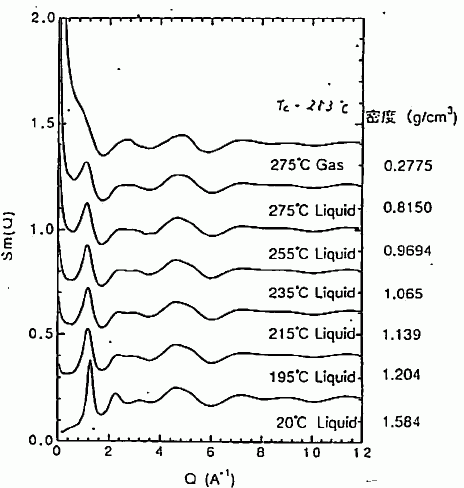
図 13. 高温低密度での、四塩化炭素の構造因子(TC = 283℃)。 実線は、実験値をなめらかにつないだもの。 |
液体四塩化炭素について、得られた構造因子を図 12 に示します。 1.3 Å-1 付近に鋭い第1ピークが現れ、 それより大きな Q に、0.203 の周りでの振動が見られます。 この 0.203 という値は、(bC2 + 4bCl2)/(bC + 4bCl)2 です。 ここでは(13)式に出てくる散乱長の平均値 < b > を、 四塩化炭素1分子あたりの平均値(この場合 bC + 4bCl)にとって解析を進めていますので、 注意してください(この意味で、図には Sm(Q) と表記してあります)。 図 12 の構造因子は、図 8 に見た単純流体のものと似かよっていますが、 振動のようすは、図 8 ほど単純ではありません。
構造因子の温度依存性に注目しますと、 温度を上げていくにつれて第1ピークが少し低波数側に移動し、 第2ピークがぼやけてきます。 もっと温度を上げ、密度の低いところになりますと、さらにパターンに変化が現れます。 図 13 に示すのは、温度を上げ、気相にまで至る領域の構造因子です。 密度が下がるにつれ、低波数(Q < 1 Å-1)の成分がどんど ん成長してきます。そして気相側の 0.2775 g cm3 にいくと、 もはや第1ピークは見えなくなってしまいます。
なおこの構造因子の Q = 0 の値は、等温圧縮率と結びつく量になります。 高い温度での PVT のデータがえられず、全部について検討したわけではありませんが、 常温付近でえられた S(0) の値は、PVT の測定から得られているものと、よく一致しています。