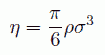◇分子配向の重要性

さてこうして出てくる構造因子と、分子の構造や相互作用との関わりをさらに解析していくことを考えます。 図 12 と 13 で見た S(Q) には、当然、四塩化炭素分子が正四面体構造を取っていることの効果が入っています。 しかしまずは大胆に、四塩化炭素分子が、互いに独立に回転する球とみなしてよいものと考えてみます。

分子が自由に回転するサイズということで、 中心の炭素原子から塩素原子のファンデルワールス球の縁までの距離を考えてみましょう。 すると C-Cl の結合距離が 1.77 Å、塩素のファンデルワールス半径が 1.8 Å ですから、 四塩化炭素は直径 7.1 Å の球ということになります。 しかしこれはおかしい。 というのは四塩化炭素の密度の値に照してみると、 この球形モデルでは、直径 σ の球を数密度 ρ で詰めた時のパッキング率

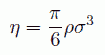　　(25)

が、三重点付近（1.59 g cm^-3）で、1.25。 1 以上になってしまうのです。 これは、四塩化炭素分子が球形からはずれている効果、 互いにある配向をとって詰っているという因子、 を何らかの形で取り込まないと、 液体構造をうまく説明できないことを意味しています。

◇四塩化炭素分子の実効的球モデル

上で考えたように、自由回転するようなモデルでは、球形近似はうまくいきません。 しかし互いにある配向をとったとしても、十分離れたところにある四塩化炭素分子同士は、 配向が平均化される結果、実効的に球と見なせるにちがいありません。 そこでまず、すべての四塩化炭素分子を、ある実効的な直径 σ_eff を持つ球と仮定して解析してみました。

四塩化炭素分子を球と仮定して計算される構造因子 S^u(Q) は、 次の式のように、分子構造（正四面体構造）からの寄与と、分子中心（この場合、炭素原子）間の構造の寄与の和で表されます。

　　(26)

ここで F₁(Q) は分子内の構造からの寄与で

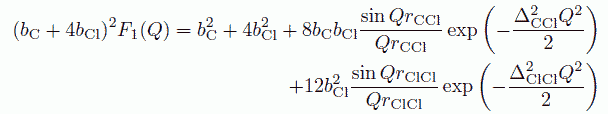　　(27)

F_u(Q) は、互いの分子間の配向を平均化し、完全に無配向とした時に出てくる因子で

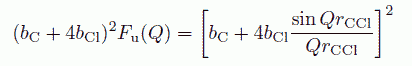　　(28)

式中、Δ_CCl、Δ_ClCl は、分子内の C-Cl、C-C 距離のゆらぎの程度を表わすパラメーターで、 Q の大きな所の構造因子を用いて決定することができます。 分子中心についての構造因子 S_C^u(Q) については、 すでに単純液体について知られているところにしたがって、(24)式で評価することにします。 S_C^u(Q) のパラメーターの設定ですが、これは S(Q) の第１ピークが再現できるように決めてやります。

◇分子配向の定量的評価

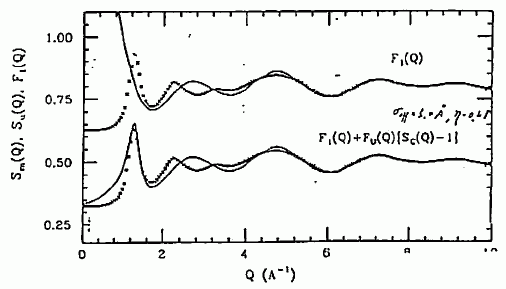
図 14. 無配向と仮定した場合の、四塩化炭素の構造因子に対するあてはめ結果。 図中×は、実験的に得られた構造因子。

無配向（球形）と仮定して計算した構造因子と、実測の構造因子とを比較してみたのが図 14 です。 Q > 5 Å^-1 の領域では、構造因子は計算値とよく一致していますが、 それよりも低波数側では一致はよくありません。 これは、近接した分子間に強い配向の相関があり、その効果が現れていると考えられます。

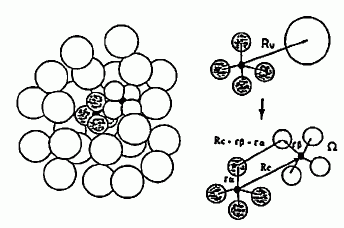
そこで、球と考えて計算した構造因子から、 本来は強く配向する分子からの寄与を取り出し、改めてそれに配向の効果を付け加えて戻す、ということをやります。 かりに、球形として計算したものの内、中心分子からの距離が R_u 付近にあるとして勘定していた n_C 個の分子が、 実は R_C 離れたところで、中心分子に対して S という配向を取っていたものとします。 すると、無配向と仮定した構造因子との差として、次式のような表現を得ます。

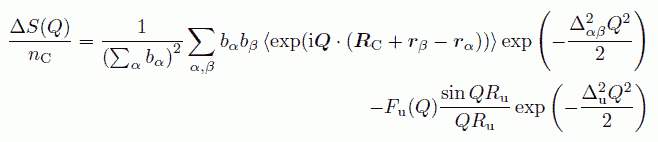　　(29)

図 15. 近接分子間の配向の設定。

ここで、α、β はそれぞれ中心分子および配向している分子に属する任意の原子を示し、 距離の揺らぎΔ_αβ、ΔR_u は、 中心間距離の揺らぎを表わすパラメーター δ_C を用いて、 次のように表されものとします。

　　(30)
　　(31)

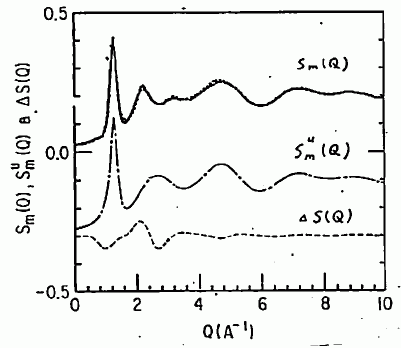
図 16. 分子配向の効果を考慮した、四塩化炭素の構造因子のあてはめ結果（-20℃）。 Sm(Q) の結果の中の・は、実験点。

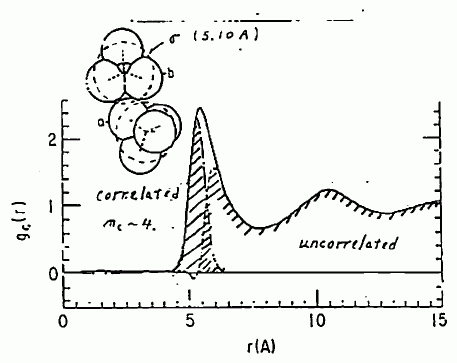
最適化したパラメーターから計算される分子配向についていいますと、 配向している分子数は約 4、そしてそれらは CCl₄ の３個の Cl 原子で作る三角形に、 もう一方の CCl₄ 分子の Cl 原子を突っ込む形の配向を取ります。 またこの時、C-Cl-C は直線ではなく、幾分曲っているという結果になります。 こうした構造を、中心間（C-C 間）の動径分布関数の形で示したのが、図 17 です。 分子の近傍 5.1 Å ぐらいのところを、配向した分子が占めているのが見て取れます。 無相関の分子の動径分布関数が、分子近傍でわずかに負の値をとるのは、 今回の取扱いの不十分さによるものですが、それもきわめて小さいものに止まっています。

図 17. 計算された、四塩化炭素の分子中心間の動径分布関数（-20℃）。

◇配位数の密度依存性

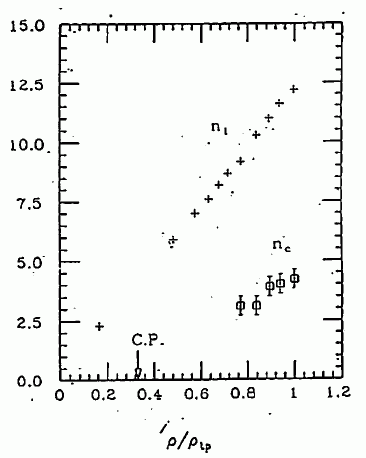
図 18. 四塩化炭素の配位数（n1）、および強く配向する分子数（nC）の密度依存性。 密度は三重点の密度でスケールしてある。

密度を変化させた時に、配位数および強く配向した分子の数がどう変化するかは、 興味深いところです。 この配位数を求めるというのは、かなり任意性をともなうのですが、 ここでは g(r) のくびれたところで打ち切って求めてあります。 最近接分子数は、三重点での 12 程度から、密度にほぼ比例して減少していきます。 配向している分子数も、やはり密度が小さくなるにつれ、 減っていくのですが、低密度側では決めることができません。 というのは、図 13 にもあるように、低密度側では S(Q) の第１ピークがぼけてしまって、 剛体球のサイズが決めづらくなる、というよりは、剛体球流体を参照系に取るのがよい近似でなくなるのです。 低密度領域を扱うには、参照系にレナード－ジョーンズ流体を取るなり、もっと進んだ取り扱いが必要になります。