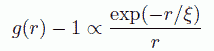◇長距離構造 ── 液体の相関距離

ここまで分子近傍の液体構造の話をしてきたのですが、 もっと長距離にわたる構造（低波数の構造）に目を向けてみましょう。 オルンシュタイン－ゼルニケの取り扱いによると、動径分布関数は十分遠方で、次のような漸近的な振る舞いをします。

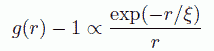　　(32)

これは構造因子でいうと、Q の小さいところで

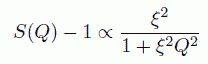　　(33)

が、成り立つことに対応します。ここで ξ は、流体中の分子同士の相関距離を示します。 これは式の形の上では、電解質溶液でいう、デバイ長さに相当するもので、臨界点に近づくにつれ、 相関距離 ξ はどんどん大きくなっていきます。

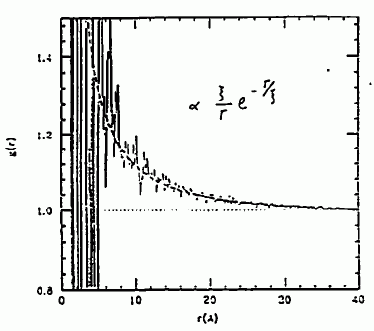
図 19. 長距離における動径分布関数のふるまい。 275℃、気相側。

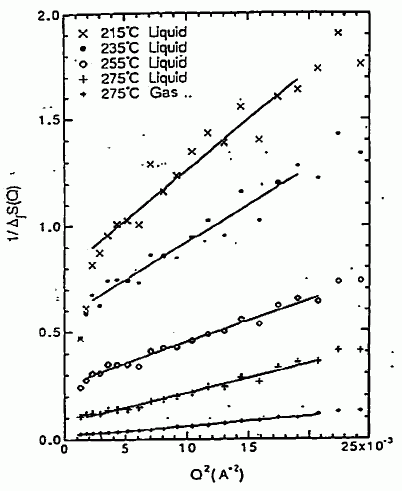
図 20. 低波数での構造因子のふるまい。

図 19 に示すのは、気相側の密度で、この漸近的な振る舞いを調べた結果です。 r > 8 Å では、相関距離 17 Å にとって、g(r) をよく説明できます。 S(Q) で見るには S(Q) の逆数をとって、それを Q² に対してプロットしてやればよいわけで、 図 20 のように、やはり Q の小さい所では、Q² に対し直線的に変化する挙動が見えています。

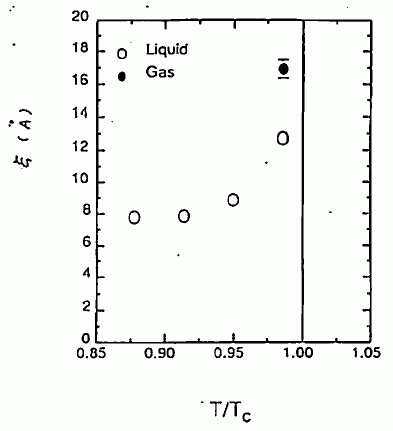
このようにして得た ξ を、温度に対してプロットしたのが図 21 です。 臨界点に近付くにつれ、相関長さが伸びていくことがわかります。

図 21. 相関距離の密度依存性。

◇液体の密度揺らぎを評価する

こうして、流体を特徴付ける長さ > が得られたわけですが、 これを用いて、密度揺らぎを具体的な形で表現することを考えます。 通常、ある体積中の粒子数の揺らぎについて、次のような表式が用いられています。

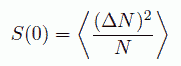　　(34)

(34)式から、粒子数の揺らぎは、考える体積に含まれる粒子数の平方根に比例して小さくなることがわかります。 しかしこうした立場からは、揺らぎは系のサイズに依存し、 「液体はどの程度揺らぐか？」という問い掛けに、十分応えられません。 そこで、上で得た、液体を特徴付ける長さ > を用いて、系のサイズに依存しない、 液体固有の密度揺らぎを評価することを考えました。 それには、流体中のある相関をもって挙動する領域の体積 V_f を、

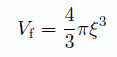　　(35)

で評価し、(34)式を、

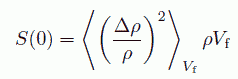　　(36)

と書き換えることによって、V_f 中の密度の揺らぎ <( δρ/ρ)² > V_f を計算すればよいはずです。 図 22に示したのは、こうして評価した密度揺らぎの、密度依存性です。 気相から液相に行くにしたがって、密度揺らぎが減少して行くことが見て取れます。 このように評価した密度ゆらぎが臨界点でどのような値をとるかは、 興味ある問題ですが、それは今後の実験に待ちたいと思います。

先の密度揺らぎから得られる、気相、液相での密度揺らぎの定性的な描像を最後に示します。 気相では密度は 40 % 近く揺らぐのに対し、液相では 17 % 程度、かつ相関距離も 13 Å と短くなっています。

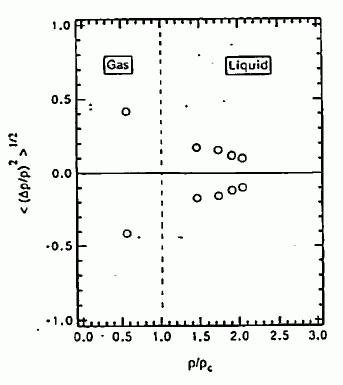
図 22. 気相から液相域にいたるまでの、四塩化炭素の密度揺らぎの変化。

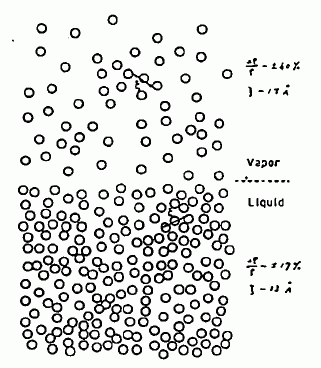
図 23. 気相と液相での密度揺らぎの概念図。気相での密度揺らぎ Δρ/ρ = ±40 %、相関距離ξ = 17 Å。 液相での密度揺らぎ Δρ/ρ = ±17 %、相関距離ξ = 13 Å。 四塩化炭素、275℃。