|
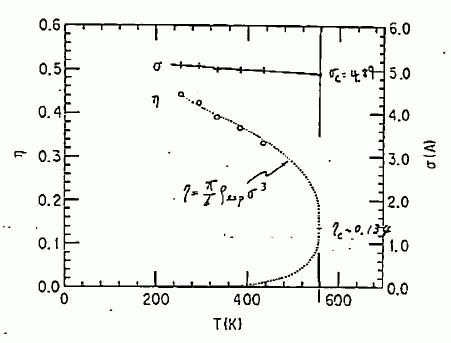
図 24. 気液共存線上での、四塩化炭素のパッキング率、 有効直径の温度依存性。 |
Q. (3)式で、散乱に寄与する原子核の数 N は、実験的にはどうやって決めるのですか?
A. N は、サンプルセルを通過する中性子線の、幅と高さから散乱に寄与するサンプルの体積を求め、 それに液体の密度をかけて計算します。 ですから、こうした実験の時には、中性子線の高さ方向はスリットにより正確に絞りますが、 幅についてはあまり絞り込まず、セルが中性子線に完浴するようにして、体積の計算の誤差を小さくするようにします。
Q. X線を用いた回折実験と比べて、中性子を用いるメリットにはどのようなものがあるでしょうか。
Q. アルカン系のものなど、細長い分子にも、今回のような取扱いは可能なのでしょうか?
A. 今の所、そんなにたくさんやっているわけではありませんので、はっきりしたことはわかりません。 ただしポリエチレンについては、解析をやって、今回と同様の手法が有効であることは、確かめています。 その時には、炭素 5 個のユニットを球だと見立て、ポリエチレンがそうした球の連なった数珠であるとして、解析を行いました。
Q. 有効直径は、状態方程式などの立場からも、結構議論されていると思います。 今回の構造因子から出てくる結果と、そうした状態方程式などで考えられている有効直径というのは、 対応する結果を与えているのでしょうか?また温度依存性は、どうなっているのでしょうか?
A. 今回得た、四塩化炭素の有効直径は、剛体球流体を参照系に使って PVT を議論している研究で用いられているものと、ほぼ一致します。 あまり高い温度で、四塩化炭素の PVT を議論している仕事はないのですが、 今回の解析でえられる有効直径は、図 24 に示しますように、 温度を上げていくと 5.1 Å から 4.89 Å まで小さくなっていきます。

|
図 24. 気液共存線上での、四塩化炭素のパッキング率、 有効直径の温度依存性。 |