|
| 図 1.1 アルゴンの部分分子容に占める並進運動の寄与 |
前節で、無限希釈量の溶質の部分分子容が、並進運動の寄与と配置の寄与とからなることを示したが、この二つが溶媒の気体から液体にいたる密度変化とともにどのように変化するかを考えてみよう。
溶媒の密度が非常に低いときには、溶質と溶媒との間の相関はきわめて小さくなる。 この一方並進運動の寄与は、圧縮率が大きくなる(粒子一個あたりの空間が大きくなる)ため大きい。 したがって、並進運動の寄与は配置の寄与に比べてきわめて大きいと考えられる。 溶媒の密度が高い場合にはこれとは逆で配置の寄与が支配的となろう。
これまでに得られている実験的な知見からこのような予想を確かめてみよう。 実際の溶液でこのような広範な密度領域について部分分子容を調べた例はまだない。 そこでここでは、純物質について少し仮想的(だが厳密)な取扱いを行なう。
今、純物質 X 中のある分子 Y が、その他の分子と何らかの形で区別がつけられたものとしよう。 ただし、この区別はなんら他の X 分子との間の相互作用には影響をおよぼさないような方法でつけられているものとする。 こうすると Y の部分分子容は体積の加成性から常に X の部分分子容に等しい。 したがって、この仮想的な分子 Y の部分分子容は
\begin{eqnarray} V_\mrm{Y} &=& \kappa_T k_\mrm{B} T - \frac{\langle \delta N_\mrm{X} \delta N_\mrm{Y} \rangle}{\langle N_\mrm{X} \rangle \langle N_\mrm{Y} \rangle} V \label{eq:1.2.1} \\ &=& \frac{V}{N_\mrm{X}} \nonumber \end{eqnarray}
で与えられることになる。 実験的に純物質の \(PVT\) 性質はよく知られているので \eqref{eq:1.2.1} 式の右辺の並進運動の寄与、配置の寄与それぞれを定めることができる。

|
| 図 1.1 アルゴンの部分分子容に占める並進運動の寄与 |
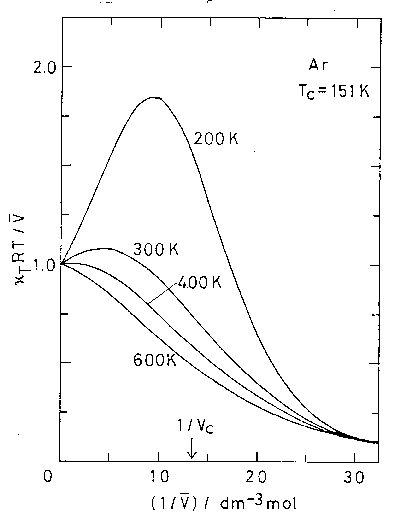
図 1.1 にアルゴンについて、200、300、400 K における計算結果を示した。 結果は、並進の寄与を分子容 \(\bar{V}\) で割った形で示してある。 これは \(\langle (\delta N_\mrm{X})^2 \rangle/\langle N_\mrm{X} \rangle\) に相当する。 \(\bar{V}\) の中に占める並進運動の寄与は、低密度域できわめて大きく、\(\bar{V}\) はほとんど並進運動の寄与によって決まっている。 そして、低密度域から高密度域へ移行するにしたがい、最初、部分分子容にしめる並進運動の寄与は増大するが、中密度域で最大値に達した後減少に転じ、 高密度域ではその部分分子容にしめる比率は10 %程度にまで落ちてしまう。 一方、配置の寄与は低密度域では負の値をとり、その大きさは全体の部分分子容に比して問題にならないほど小さい。 そして、低密度域から高密度域へ移行するにしたがい、まず減少し中密度域で最小値に達した後増大に転じて正の値をとるようになり、 高密度域ではその部分分子容にしめる比率は90 %程度と高密度域での部分分子容はこの配置の寄与で決まることになる。 ここに示したのは、それぞれの寄与を部分分子容でスケ-リングした結果であるが、スケ-リングしないそのままの量をもってきても同様の傾向がえられる。 こうして上で述べた大まかな予想は確かめられたわけである。 ここで見られた中密度域でのふるまいは、もう少し温度を下げたときには臨界点(アルゴンの臨界温度 151 K, 臨界密度 13.4 mol dm-3)におけるふるまいへとつながることになる。 このような、気体の部分分子容は並進運動の寄与が決め、液体の部分分子容は配置の寄与が決める、という結果は、気体においては溶質の部分分子容がその溶質の個性を反映せず、 液体では個性を強く反映するということに対応している。 このことはまた、気体における議論の安易な"外挿"が液体の議論には届かない、ということを告げるものでもある。(詳細については3章で再び論じる)
前節までに、部分分子容についての表現をみた。 ここではいよいよ、体積変化についての形式論を考えることにしよう。 ここでは簡単のため、ただ一つの化学反応が起きるものとする。 1.2節において触れたように、溶質(反応物、生成物)の濃度が高い場合には、溶質分子間の相関を考慮せねばならず、取り扱いが難しい。 以下ではすべて無限希釈状態における化学反応を考えることにする。 これはまた、溶液化学において一般に行なわれる標準状態の取り方に対応している。 化学反応は一般に次のように書ける[1.3]。
\begin{equation} 0 \rightleftarrows \Sigma \nu_i [i] \label{eq:1.3.1} \end{equation}
ここで、\(\nu_i\) は成分 \(i\) の化学量論係数、 \([i]\) はその化学式である。 これに従うと、たとえばメタンの燃焼は、
\begin{equation} 0 \rightleftarrows \mrm{- CH_4 - 2O_2 + CO_2 + 2H_2O} \label{eq:1.3.2} \end{equation}
となる。 ここで、化学量論係数に負の値も許していることを留意されたい。 いわゆる反応進行度 \(z\) は化学反応による各成分の粒子数変化 \(\Delta N_i\) によって
\begin{equation} z = \frac{\Delta N_i}{\nu_i} \label{eq:1.3.3} \end{equation}
で定義される。
開かれた系における化学反応では、外部からの粒子の流入による変化と、化学反応による粒子の生成による変化とが共存することから取扱いがやっかいである。 したがって、まず閉じた系についての議論から始めることにする。 これはまた、ふつう行なわれる化学反応についての熱力学的議論と軌を一にするものでもある。
閉じた系で化学反応にともなう体積変化 \(\Delta V\) は、次のようにあらわされる。
\begin{equation} \Delta V = \pdifA{V}{z}{T, P} \label{eq:1.3.4} \end{equation}
ここで、体積の微小変化が
\begin{eqnarray} \delta V &=& \pdif{V}{T} \delta T + \pdif{V}{P} \delta P + \Sigma \pdif{V}{N_i} \delta N_i \nonumber \\ &=& \pdif{V}{T} \delta T + \pdif{V}{P} \delta P + \Sigma V_i \delta N_i \label{eq:1.1.5} \end{eqnarray}
で表わされることから、\(\partial N_i/\partial z = \nu_i\) であることに注意して、
\begin{equation} \Delta V = \Sigma \nu_i V_i \label{eq:1.3.6} \end{equation}
をえる。 ここで開かれた系での議論に移って、ある体積中の粒子数のゆらぎの立場からながめてみれば、無限希釈において、これは(1.1.6)式によって
\begin{equation} \Delta V = \Sigma \nu_i \kappa_T k_\mrm{B} T - \left \langle \delta N_\mrm{S} \sum_i {\frac{\nu_i \delta N_i}{\langle N_i \rangle}} \right \rangle \frac{V}{\langle N_\mrm{S} \rangle} \label{eq:1.3.7} \end{equation}
と表現できる。 ここで、下付き S は溶媒をあらわす。 この式中のゆらぎの表現を応答関数のかたちで書き直すと、もう少しきれいな表現ができる。
このためには、
\begin{eqnarray} \frac{\langle \delta N_\mrm{S} \delta N_i \rangle}{\langle N_i \rangle} k_\mrm{B} T &=& \left( \pdif{\ln \langle N_i \rangle}{\mu_\mrm{S}} \right) \nonumber \\ &=& \left( \pdif{P}{\mu_\mrm{S}} \right) \left( \pdif{\ln \langle N_i \rangle}{P} \right) \nonumber \\ &=& \frac{\langle N_\mrm{S} \rangle}{V} \left( \pdif{\ln \langle N_i \rangle}{P} \right) \label{eq:1.3.8} \end{eqnarray}
に注意する。 こうすると、粒子数ゆらぎの表現を圧力に対する応答の形に引き直すことができ、
\begin{eqnarray} \Delta V &=& \Sigma \nu_i \kappa_T k_\mrm{B} T - k_\mrm{B} T \sum {\nu_i \left( \pdif{\ln \langle N_i \rangle}{P} \right)} \nonumber \\ &=& \Sigma \nu_i \kappa_T k_\mrm{B} T - k_\mrm{B} T \left( \pdif{\ln K}{P} \right) \label{eq:1.3.9} \end{eqnarray}
という表現がえられる。ここで、\(K\) は
\begin{equation} K = \prod \left( \frac{\langle N_i \rangle}{V} \right) ^{\nu_i} \label{eq:1.3.10} \end{equation}
であり、カノニカルな系における平衡定数に相当する。 ただし、\eqref{eq:1.3.9}式において考えられている \(K\) は開かれた系についてのもので、外部との粒子のやりとりがある結果必ずしも「定数」ではない。 \eqref{eq:1.3.9} 式の第二項の圧力微分は温度、体積、反応物の化学ポテンシャルを一定に保った条件でとっている。 カノニカルな系における表現では、この微分は反応物の化学ポテンシャル一定の条件をはずした形で与えることができる。 これは閉じた系が化学平衡にあるとき化学親和力がつねに0となることから許されることである。 ここで化学親和力 \(A\) は次の式で定義される量である。
\begin{equation} A = -\sum \nu_i \mu_i \label{eq:1.3.11} \end{equation}
化学平衡で化学親和力が0になることは直接化学反応進行度に対応する外力が存在しないことによっている。 このため \eqref{eq:1.3.9} 式までで考えたような開かれた系において化学親和力が0でないところに系を保つ際には化学反応にともなう粒子数変化を補うために、 つねに粒子の流入、流出を行ない一種の定常状態を実現していることになっている。
この化学親和力がつねに 0 になるような設定の下(つまり、一般に行なわれるカノニカルな系の場合)で、 \eqref{eq:1.3.9} 式の圧力微分における反応物の化学ポテンシャル一定の条件をはずすことができることを示そう。 まず温度・体積一定の条件下、次の式に注目する。
\begin{eqnarray} \frac{\rmd N_i}{\rmd P} &=& \pdifA{N_i}{P}{\mu_i} + \pdifA{N_i}{\mu_i}{P} \frac{\rmd \mu_i}{\rmd P} \nonumber \\ &=& \pdifA{N_i}{P}{\mu_i} +\frac{N_i}{k_\mrm{B} T} \frac{\rmd \mu_i}{\rmd P} \label{eq:1.3.12} \end{eqnarray}
ここで、反応物は無限希釈の状態にあり互いの相関は無視できることを用いた。 ここで、\eqref{eq:1.3.12}式の両辺を \(\langle N_i \rangle\) で割り、次式をえる。
\begin{eqnarray} \sum {\nu_i} \frac{\rmd \ln \langle N_i \rangle}{\rmd P} &=& \sum {\nu_i} \pdifA{\ln \langle N_i \rangle}{P}{\mu_i} + \frac{1}{k_\mrm{B} T} \sum {\nu_i} \frac{\rmd \mu_i}{\rmd P} \nonumber \\ &=& \sum {\nu_i} \pdifA{\ln \langle N_i \rangle}{P}{\mu_i} - \frac{1}{k_\mrm{B} T} \frac{\rmd A}{\rmd P} \label{eq:1.3.13} \end{eqnarray}
ここで\eqref{eq:1.3.13}式の第二項は上の条件から0であり、開かれた系における化学ポテンシャルを一定におさえた表現は閉じた系における表現と一致することになる。
\eqref{eq:1.3.9}式において、この式の右辺第一項がはっきりした化学的な意味付けをもって登場していることに注目したい。 この項の意味については、先の部分分子容の組立てにおける議論と同じ議論ができる。 つまり、これは導出で用いた熱ようどう理論からは化学反応が起きたことによる溶媒の化学ポテンシャルの変化に対応する量であり、 またカノニカルな系からの考察では容器の壁と反応物との直接の相互作用の変化、並進運動の寄与の変化に対する体積の応答である。
従来の議論においては、この項は単に体積モル濃度 molarity で平衡定数が表現されているがゆえの補正という程度にしか認識されていなかった[1.4]。 おそらくこれは、モル分率であらわされた平衡定数に対する扱いが一般に化学熱力学においてひろく行なわれていることによるのであろう。 この場合には圧力微分する際にこの項があからさまな形で表面に出てこない。 認識されていることは少ないようだが、モル分率であらわした平衡定数を微分するとき次のような操作が行なわれているのである。 無限希釈においてある成分 \(i\) のモル分率 \(x_i\) は
\begin{equation} x_i = \frac{N_i}{N_\mrm{S}} \label{eq:1.3.14} \end{equation}
で表わされる。これを用いた平衡定数 \(K_x\) は
\begin{equation} K_x = \prod x_i^{\nu_i} \label{eq:1.3.15} \end{equation}
である。これを圧力微分すると
\begin{eqnarray} \pdif {\ln K_x}{P} &=& \pdif {\ln K}{P} - \sum {\nu_i} \pdif{\ln N_\mrm{S}}{P} \nonumber \\ &=& \pdif {\ln K}{P} - \sum {\nu_i} \kappa_T \label{eq:1.3.16} \end{eqnarray}
となる。 これを \eqref{eq:1.3.9}式に代入すると第一項は打ち消される。 つまり、モル分率であらわした平衡定数では、溶媒の粒子数に対する微分が \eqref{eq:1.3.9}式のようにあからさまな形では出てこないのである。 その点体積モル濃度であらわした平衡定数は溶媒の化学ポテンシャル変化に対応する項を含まない結果、前節まででみた部分分子容の組立てをより忠実にあらわしたものといえよう。