|
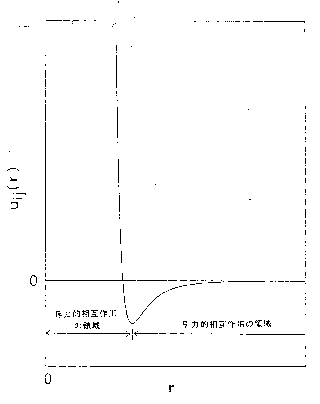
| 図 3.1 分子間相互作用のプロフィル |
1、2章で体積変化にかかわるさまざまな諸量の形式論を展開した。 本章では、分子のなりたちに踏み込んで液体の構造と体積変化の関わりを検討する。
液体、溶液中において分子は多数の分子と相互作用している。 溶液中で、ある分子対 A-B の間に働く力に注目することにしよう。 このとき周りの分子はいわば A-B の相互作用の場を提供してくれているものと考える。 すると AB 両者の間に働く力は、AB 間の距離の微小な変化にともなうポテンシャルエネルギ-変化で表現される。 こうしてえられる AB 対の間に働く力は、周りに他の分子がどのように配置しているか、またその AB 間の微小な距離の変化にともなってそれらの配置がいかに変化するかに依存する。 したがって、一般に溶液中のある分子の対に注目してその間に働く「固有の力」を純粋に取り出すことはできない、 あるいは操作主義の立場からはそのような「固有の力」といった概念は意味を持たないのである。 しかし、こういった多体の相互作用の背景になんらかの構成要素、実体があると考えることによってその系をよりよく理解できるならばそれを拒否すべき理由はない。 このような立場から最もよくとられるのは、全系のポテンシャルエネルギ-が分子対ごとに割り当てられるポテンシャルエネルギ-の和であるとする行き方、対ポテンシャルエネルギ-近似である。 つまり式で書けば
\begin{equation} U = \sum_{i \lt j} u_{ij} \label{eq:3.1.1} \end{equation}
となる。 ここで、\(u_{ij}\) は \(i\) 番目と \(j\) 番目の粒子からなる対が他の粒子と相互作用を持たない場合の相互作用エネルギ-である。 これはまた溶液中において \(i~j\) 二分子間に働く分子間力が、 \(i~j\) 間の直接の相互作用と周りの溶媒分子を通じての間接の相互作用に分けられるとする考え方でもある。
これまでこの対ポテンシャルエネルギ-近似に基づいて多くの結晶・液体について考察が行なわれてきた[0.7]。 また近年さかんに行なわれている計算機シミュレ-ションのほとんどすべてはこの近似に基づいている。 このような中でえられた液体に対する描像は十分満足すべきものでありこの近似の妥当性を裏付ける。 さらに、従来行なわれてきた溶媒-溶媒・溶質-溶媒・溶質-溶質相互作用という形で相互作用を捉えようとする溶液現象の理解の枠組も、この線上にあることを指摘しておかねばならないだろう。 本研究もこの対ポテンシャルエネルギ-近似に基づいて実際の系についての考察を行なう。

|
| 図 3.1 分子間相互作用のプロフィル |
前節のように設定された分子間の対ポテンシャルエネルギ-は、一般に近距離で働く斥力領域と遠距離で働く引力領域とからなる。 図 3.1 にそのおおまかなありさまを示した。 このポテンシャルエネルギ-の距離微分によって分子間力がえられる。 斥力はきわめて大きくその働く領域はきわめてせまい。 そして引力は斥力にくらべて弱く、働く領域は遠くにまでおよんでいる。 このしごく当然にみえることが、後述する液体に対するファンデルワ-ルスの描像を妥当させている。 この節では、分子間力の組立てを論じとくに従来から言われてきたファンデルワ-ルス体積・本質的体積の妥当性を検討する。
これまで、分子間に働く力を記述するのに用いられてきたものにファンデルワ-ルス半径という考えがある。 この考えの根底には分子にはそれぞれ固有の大きさ・ひろがりがある、とする考えが横たわっている。 いま、A、B 二分子それぞれに割り当てられた固有のひろがり(以下では分子のコアとも呼ぶことにする)を \(C_\mrm{A}\)、\(C_\mrm{B}\)とする。 この主張に基づけば AB 間のポテンシャルエネルギ-は次のように書ける。
\begin{equation} u_\mrm{AB}(r, \vec{q}_\mrm{A}, \vec{q}_\mrm{B}) = \left \{ \begin{array}{l1} \infty & (C_\mrm{A} \cap C_\mrm{B}) \ne \Phi \\ 0 & (C_\mrm{A} \cap C_\mrm{B}) = \Phi \end{array} \right . \label{eq:3.2.1} \end{equation}
ここで \(r\) は AB 間の距離、\(\vec{q}_\mrm{A}\)、\(\vec{q}_\mrm{B}\) はそれぞれ A、B の分子の配向(分子にかたちがあると見ていることに注意)を示す。 また \((C_\mrm{A} \cap C_\mrm{B})\) は考える分子の配置において AB 二分子の固有のひろがりの重なりをあらわし、 \(\Phi\) は重なりがないことを示す。 球対称の場合にはもっと具体的に次のようになる。
\begin{equation} u_\mrm{AB}(r) = \left \{ \begin{array}{l1} \infty & r \le r_\mrm{A} + r_\mrm{B} \\ 0 & r \gt r_\mrm{A} + r_\mrm{B} \end{array} \right . \label{eq:3.2.2} \end{equation}
ここで \(r_\mrm{A}\)、 \(r_\mrm{B}\)はそれぞれ A、B のファンデルワ-ルス半径とよばれる量である。
このような想定が実際に成立するかどうかを確かめるには球対称分子 A、B をとり、 AA、BB、AB それぞれの相互作用を測定して最近接分子間距離 \(r_\mrm{AA}\)、\(r_\mrm{BB}\)、\(r_\mrm{AB}\) を求め
\begin{equation} r_\mrm{AB} = \frac{r_\mrm{AA} + r_\mrm{BB}}{2} \label{eq:3.2.3} \end{equation}
が成立するかどうかを調べればよい。 すでにこれについては結晶などで成立が確かめられておりこの考えは広く受け入れられているように思われる[3.1]。
このような、分子それぞれに固有の大きさ・ひろがりを割り当てて分子間力を議論する行き方は、 巨視的な物体に対してほとんど意識することなく用いられているところのものを分子レベルにまで拡張したものである。 われわれが巨視的なレベルで物体の大きさを測るとき、用いる物差しはいくらでも滑らかなものになることを暗黙の前提としている。 しかし、分子レベルの問題においては部分分子容でみたような問題が現われてくる。 つまり、固有の大きさ・ひろがりは、いかに観測されるのかという問題である。 固有の大きさが0であるような物体はここでは存在しないのである。
|
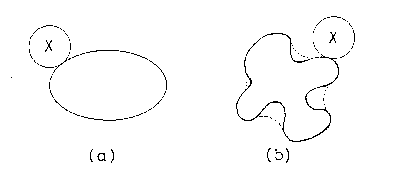
図 3.2. 分子コアの決定に関わる不確定の要素。 いずれも実線は、大きさを無視できる作用分子 X を用いて決めた分子コア。 作用分子 X が大きさを持つようになると、凸体である (a) の場合には大きさのない作用分子と同じ結果を与えるが、 (b) の場合には点線のように分子コアとしてより大きなものを与える。 |
上で、固有の大きさ・ひろがりの存在を確認するために球対称の分子間のポテンシャルエネルギ-を測定すればよいことを述べた。 この場合には固有の大きさが 0 であるような物体を想定する必要はもうとうない。 さらに、いわゆる凸体については球対称の分子をそれと相互作用させ、その球面の包絡線をもってこの凸体固有の大きさと定義することができる(図 3.2a)。 しかし一般には対象とするものが形を持つ場合に測定する道具となる物体に大きさがある限り、固有の大きさ・ひろがりを一意的に決定できない場合が生じる。 実際図 3.2b のような場合には凸体と同じようにして固有の大きさを決めようとしても、どのようなサイズの球を持って来るかによって分子固有の大きさは変化する。 つまりこの場合、測定手段によって観測にかかる固有の大きさは変化するのである。
こうした問題は巨視的な物体においても現われる。 たとえばスポンジの体積を求めることを考えよう。 スポンジを段ボ-ル箱に詰めるときにはその外面の寸法からわれわれはスポンジの体積を割り出し箱に何個入るか計算する。 しかし、水の中に沈めたスポンジの占める体積を求めるときには、水槽につけどれだけ水かさが増えるかで体積を決める。 当然、水に沈めたときの方が体積として小さな値を与える。 つまり段ボ-ル箱に詰めるときのように対象がスポンジの孔よりも十分大きい場合と、 水に沈めるときのように対象がほぼ連続体とみなしうるような場合とで大きさ・ひろがりが異なるのである。 この巨視的な場合についての考察からも明らかに、問題は「分子固有の大きさはどれだけか」ではなく、 「それを想定することによって分子間相互作用がよりよく理解できるか」そしてもしそうならば、「それはいかに観測されるか」にあるのである。
固有の大きさ・ひろがりといった概念は、われわれが日常接する物体のイメ-ジを分子の世界にまでそのまま外挿したものである。 このようなものを想定することによって、われわれはあたかも分子が巨視的な物体であるかのように分子間の相互作用を扱うことができ、 分子間相互作用を理解するより親しみ深い枠組を組立てることができる。 これが結晶の最近接分子間距離のデ-タや気相における分子の挙動からも支持されることを思えばなおさらのことであろう。 しかしこの一方でそれはあくまで机の上の概念に過ぎず、われわれが何らかの形で測定するものにそのまま対応しないことに注意すべきである。 0 章でも述べたように、従来の体積変化の化学はあたかも観測される体積変化にこの分子固有の体積の変化が生のまま反映されるという誤った思いこみから途方もない混乱と貧困をもたらしたのであった。
液体における最近接分子間の平均距離はその液体を形作る分子の大きさの程度である。 たとえば水の分子容はおよそ 18 cm3 mol-1 であり、 もし水分子が単純立方格子を組んでいるとすればその距離はおおよそ 0.3 nm 程度、ほぼ水の“大きさ”としていわれる値と同程度になる。 このことは、液体中において斥力的な相互作用が支配的に働くであろうことをもの語る。 これに対して気体中では分子間距離が大きく、引力的な相互作用が支配的となる[0.8]。
これは1章3節で、注目する分子と溶媒分子との相関を見たときにはっきり現われていた。 図 1.1 で全体の密度が低いとき溶質・溶媒の粒子数の相関は負であるのにたいして、密度の高い領域では正になる。 つまり、密度が低いときには溶質 X と溶媒 S はあい伴って運動している結果、X が減少するときには S が減少し、X が増大するときには増大する。 これは、X と S とが引力的相互作用で結ばれていること、つまり引力的相互作用が支配的であることに相当する。 この一方、密度の高い領域では X と S とは互いに反発しあって存在している。 X が減少すればこれまで X にはじき飛ばされていた S が流入してくる、つまり、X と S との粒子数の相関は負となる。 すなわち高密度=液体領域においては斥力的相互作用が支配的なのである。 これは、上で行なった分子間の平均距離による単純な考察と一致する。
この描像は統計力学の表式でいえば、カノニカルな系の配置積分 \(Q\)
\begin{equation} Q = \int f(\epsilon) \exp(-\epsilon / k_\mrm{B} T) \rmd \epsilon \label{eq:3.3.1} \end{equation}
をとるさいに指数部分ではなく、それぞれのエネルギ-状態のスペクトル密度 \(f(\epsilon)\) が支配的な要因となることでもある。 とりわけ先にみたような剛体的相互作用のみからなる系では全ポテンシャルエネルギ-は 0 か無限大かである。 したがって \(Q\) は積分の表式から状態ごとの和に移行させることができ、エネルギ- 0 のスペクトル密度そのものになる。 このことは、斥力的相互作用の支配的な系ではエネルギ-スペクトルの密度が重要であるという上の指摘を裏付ける。
液体のファンデルワ-ルス描像は結局、このスペクトル密度が液体を理解する鍵であることを教えている。 これまでの液体・溶液の化学においては引力的相互作用にあまりに片寄った理解が多かった。 従来の体積変化の解釈では斥力的な相互作用に対する配慮は結局のところ「立体効果」というカテゴリ-に押し込められ、 斥力的相互作用に対する考慮は棚上げしておいて溶質・溶媒の相互作用といえば、イオン-双極子の相互作用、あるいは水素結合といった引力的なもののみが想定されていた。 このような状況は早急に改められねばならない。
本研究においては以下、このファンデルワ-ルス描像にしたがい斥力的相互作用にしぼって考察を行なう。 さらに、斥力的相互作用が実際に分子間に働く領域はきわめて狭いので(つまり斥力部分のポテンシャルエネルギ-の立上りがきわめて急なので)、 これを剛体的なものと置き換え、先の分子コアで分子間力をもっぱら考えることにする。