|
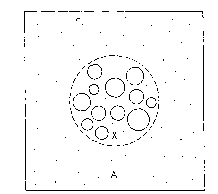
| 図 3.3. 質点からなる系A中に置かれた剛体分子からなる系X。 Xは質点のみを通す柔らかい半透膜でしきられ、 Xの中に質点は入って来れるがX中の大きさを持った剛体分子はAには入れない。 |
本研究では、以下剛体的相互作用のみからなる系についてしばしば取扱うことになる。 そこでここでは、簡単にその熱力学的性質を見ておくことにする。
出発点は、剛体的相互作用のみからなる系では相互作用エネルギ-が常に 0 となることである。 このことから \(U\) の体積についての微分は 0 であり次の関係が成立する。
\begin{equation} \pdifA{U}{V}{T} = T \pdifA{P}{T}{V} - P = 0 \label{eq:3.4.1} \end{equation}
これは粒子数を一定に保っての微分であるが当面粒子数変化は問題にしないのでア-ギュメントにはあえて書いていない。 \eqref{eq:3.4.1} 式から、次の関係がえられる。
\begin{equation} \pdifA{P}{T}{V} = \frac{P}{T} \label{eq:3.4.2} \end{equation}
\begin{equation} \frac{P}{T} = f(V, N) \label{eq:3.4.3} \end{equation}
ここで、\(f(V,N)\)は体積と粒子数のみの関数である。 つまり剛体的相互作用からのみまる系の圧力と温度の比は体積と粒子数が決まるとある値に定まる。 このことから部分分子容に関する諸量にもある制約が課せられていることを容易に示すことができる。
まず、等温圧縮率については
\begin{equation} \kappa_T = \frac{1}{V} \pdifA{V}{P}{T} = -\frac{1}{V T} \pdifA{V}{(P/T)}{T} = \frac{1}{T} h(V, N) = \frac{1}{P} f(V, N) h(V, N) \label{eq:3.4.4} \end{equation}
という関係がえられる。 ここで、\(h(V,N)\) は \(f(V,N)\) と同様体積と粒子数のみの関数である。 つまり、体積、粒子数一定の条件の下で剛体分子からなる系の圧縮率は、温度上昇、あるいは同じことだが圧力の上昇にともない、それらに反比例して減少するのである。 このことは部分分子容に対する並進の寄与 \(\kappa_T k_\mrm{B} T\) が体積と粒子数のみによって決まり温度・圧力によらないということでもある。 同じように部分分子容も温度・圧力に直接依存しないことが示せる。
\begin{equation} V_i = \kappa_T V \pdifA{P}{N_i}{T, V, N_{j \ne i}} = \kappa_T V T \pdifA{(P/T)}{N_i}{T, V, N_{j \ne i}} = v_i (V, N) \label{eq:3.4.5} \end{equation}
結局、剛体球流体について重要なのは体積・粒子数をいかに設定するかであり、温度・圧力は無関係なのである。
さらに分布関数も体積・粒子数のみの関数となる。 このことは、さまざまな配置の間の移行にともなう体積変化が体積のみの関数であること(体積変化は部分分子容の差である)、 つまり分布関数の圧力微分が体積・粒子数のみの関数であることから明らかである。 (\( P \rightarrow 0, V \rightarrow \infty\) で \(g(r) \rightarrow 1\) であることに注意されたい)
これらのことは結局、前節で述べたように剛体分子からなる系においてはエネルギ-スペクトルの密度のみによって配置積分が表現できることに対応している。
さてこのような目からもう一度、図 1.1 の並進の寄与が部分分子容に占める比を見直してみよう。 剛体分子からなる系では\eqref{eq:3.4.4}および\eqref{eq:3.4.5}式からこの \(\kappa_T k_\mrm{B} T/V\) は温度によらず一定でなければならない。 図 1.1 では“中密度”の領域でこれは大きな温度依存性を持っており、高密度域、液体に相当する領域では温度依存性はほとんど失われている。 これは中密度領域においてはファンデルワ-ルス描像が破綻していることを示す一方で、われわれが注目する液体領域ではファンデルワ-ルス描像がきわめてよく成り立つことの証明でもある。
なお図 1.1 からは、温度が高くなれば高くなるほど \(\kappa_T k_\mrm{B} T/V\) の温度依存性が失われていくことも見てとれる。 本研究では述べないが、これはファンデルワ-ルス描像が流体系に対するいわゆる高温展開という摂動論的アプロ-チと結び付くことに対応している[0.8]。
剛体分子からなる流体においてはさまざまなエネルギ-状態を考える必要がなく、問題の所在を見通しよく与えてくれる。 部分分子容を決めるために必要な手続きを確認する意味で部分分子容を理解する上の困難を論じる前に、 まず剛体分子からなる流体中における質点の部分分子容についての厳密な結果を与えることにしよう。 質点については3.2節で考えた分子固有のひろがりは一点で示される。 このことから安易に質点の部分分子容は「並進運動に要する体積」であるかのごときことが空想されたこともある。

|
| 図 3.3. 質点からなる系A中に置かれた剛体分子からなる系X。 Xは質点のみを通す柔らかい半透膜でしきられ、 Xの中に質点は入って来れるがX中の大きさを持った剛体分子はAには入れない。 |
図 3.3 のように、大きさを持った剛体分子からなる系Xが質点からなる系Aの中に、 質点は通すがX中の大きさを持った剛体分子は通さない柔らかい半透膜によってしきられて存在しているとしよう。 こうするとAに存在する質点の数の期待値 <NA>とXに存在する数の期待値 <NX>の比は
\begin{equation} \frac{N_\mrm{X}}{N_\mrm{A}} = \frac{V_\mrm{X}-V_\mrm{C}}{V_\mrm{A}} \label{eq:3.5.1} \end{equation}
に等しい。 ここで \(V_\mrm{X}\)、\(V_\mrm{A}\) はそれぞれ系 X,A の体積 \(V_\mrm{C}\) は X 中の剛体分子のコアの体積の総和である。 質点の場合には、X 中の剛体分子の配置のいかんを問わず \(\langle N_\mrm{X} \rangle\ が一定であることに注意されたい。 このように“平衡定数”がえられれば、1.3節に述べたようにして A から X への移行にともなう体積変化を次のようにえることができる。
\begin{eqnarray} \Delta V &=& -k_\mrm{B} T \pdif{\ln [\langle N_\mrm{X} \rangle/\langle N_\mrm{A} \rangle]}{P} \nonumber \\ &=& -\kappa_T^{\mrm{A}} k_\mrm{B} T + \frac{V_\mrm{X}}{V_\mrm{X} - V_\mrm{C}} \kappa_T^{\mrm{X}} k_\mrm{B} T \label{eq:3.5.2} \end{eqnarray}
ここで\(\kappa_T^{\mrm{A}}\)、\(\kappa_T^{\mrm{A}}\) はそれぞれ系 A、系 X の圧縮率である。 質点からなる流体 A において質点の部分分子容は並進の寄与 \(\kappa_T^{\mrm{A}} k_\mrm{B} T\) のみからなる。 したがって、X 中における質点の部分分子容 \(V_\mrm{p}\)はこれに \eqref{eq:3.5.2}式の体積変化を加え、
\begin{equation} V_\mrm{p} = \frac{V_\mrm{X}}{V_\mrm{X} - V_\mrm{C}} \kappa_T^{\mrm{X}} k_\mrm{B} T \label{eq:3.5.3} \end{equation}
となる。 これは1 章 1 節で \(V_\mrm{X} - V_\mrm{C}\) という大きさの箱の中に相互作用しない粒子を入れたときの圧力増加が \(k_\mrm{B} T/(V_\mrm{X} - V_\mrm{C})\) であることからも導くことができる。 ここでいう \(V_\mrm{X} - V_\mrm{C}\) は従来の枠組でいえば加えた質点の「自由体積」に相当するわけだが、 それはそのままの形でわれわれの観測する部分分子容に反映されるものでないことは明らかである。
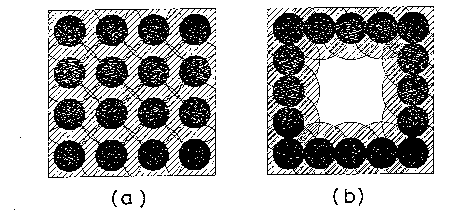
さて質点の部分分子容を考えるさいには(剛体分子流体の圧縮率は不問に付されたままではあるが)上のようにきわめて簡単にその表現をえることができた。 このように質点の場合が簡単に扱えた原因は、質点が X に存在する確率が X 中の剛体分子の配置によらず一定であったからである。 もし部分分子容を考えようとする剛体分子のコアに大きさがあったなら、とうていこのような簡単な取扱いはのぞめない。 試みに2次元の剛体円盤について、このような問題がどのように現われるかを図 3.4 に示した。 図 3.4a-b に示したような配置を溶媒たる剛体円板 X がそれぞれ占めているしよう。 注目する円板 Y がそこに受け入れられる確率は図の空白の部分の面積と全系の面積との比になる。 明らかに X の配置のいかんによって Y が受け入れられる確率は変化する。 図 3.4b では Y の受け入れられる確率は 0.15 程度であるが、 X の配置が図 3.4a のようになるとそれはもう 0 になってしまう。 こうして問題は、結局、図の空白の部分の面積を X のさまざまな配置について定めるという幾何学的問題に帰着する。 これは一見単純にみえてきわめて困難な問題であり、一般の X の配置についてこの空白部分の面積を与えることは不可能である。 3次元の場合も同じ困難がある。[補注8]
|
図 3.4. 剛体円板 X からなる2次元系。 図中の黒く塗りつぶした円は X のコア(直径 \(\sigma_\mrm{X}\))に相当する。 斜線の部分は、それぞれXを中心に描いた直径 \((\sigma_\mrm{X} + \sigma_\mrm{Y})/2\) の円であり、 ここに剛体円板 Y (直径\(\sigma_\mrm{Y}\))は入ることができない。 (a) の場合には Y をこの中に投入したとして、その化学ポテンシャルは無限大になるが、(b) の場合にはある有限の値になる。 (この系と接する Y からなる系の化学ポテンシャルを考えられたい) なお、(a)はちょうど液体の細胞モデルで、それぞれの分子を格子点上に割り当てたことになっており、液体の細胞モデルの欠陥を示してくれているものでもある。 液体分子は格子点から大きくゆらぎ、(b)のような配置を取ることによって細胞モデルでは許されない Y の流入を可能にするのである。 |
このようにXの配置に依存して受け入れられる確率が複雑に変化する結果、 実際にアンサンブル平均を正確にとるにはモンテカルロ計算などの助けを借り数値的に処理するよりほかなくなる。 ここに多体問題の固有の困難があるといえよう。 剛体分子からなる系に関する数多くの議論も結局は図 3.4 にみるような面積・体積の計算である。 たかが体積、されど体積という由縁である。