|
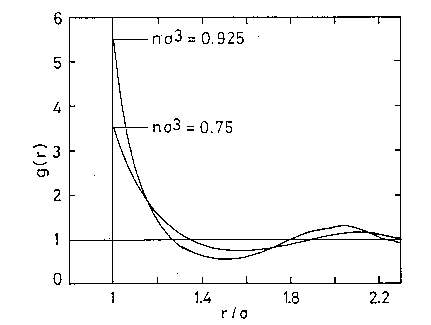
図 4.2. 剛体球流体の動径分布関数[4.2]。 図中 \(n\) は剛体球分子の数密度であり、\(\sigma\) は剛体球の直径。 |
図 4.2 に計算機実験からえられた動径分布関数 \(g(r)\) のありさまを示す。 動径分布関数は分子同士が接触するところに大きなピ-クをもち、さらに \(2\sigma\)の距離のあたりに小さな第二ピ-クがある。 これらの構造は密度を高めると一層顕著になる。 この動径分布関数の大まかな様相は実在の液体についてX線回折の結果などからえられるものとよく一致しておりファンデルワ-ルス描像の妥当性をもの語る。 分子間力を剛体的な相互作用に置き換えたことによる実在の液体の動径分布関数との最大の相違は最初のピ-クの形にあらわれる。 実在の液体では、第一ピ-クからより短い距離に向かって見たときにピ-クの落ちかたが剛体球流体と異なり緩やかである。 これは実在分子の斥力部分がほぼ剛体的と考えてよい挙動を示すものの、それに加えてある程度の無視できない柔らかさを持っていることによる。 図 4.2 に見る剛体球流体の鋭い落ち込みは、実在の分子の斥力を剛体的相互作用に置き換えたことから生まれたものであり、一般に剛体分子からなる流体の分布関数の特徴でもある。
図 4.2 に示されるような粒子分布において、注目する分子の近傍で動径分布関数が大きな値を取ることに注目したい。 これは、仮にベンゼン溶媒中でシクロペンタジエンと無水マレイン酸の Diels-Alder 反応を行なう際、 シクロペンタジエン分子の周囲の無水マレイン酸濃度は両者の間に特殊な引力がなくとも溶液全体の平均の濃度より数倍高くなっているということを告げるものである。 このような構造は二体の間の相互作用はこの場合 \(\sigma\) よりも遠くへはおよばないから、周りの分子との多体的な相互作用に由来するものであることは明らかである。
この挙動には分子間に働く力という視点から眺めることによって、きわめて直観的な説明を与えることができる。 分子間に働く力は3.1節で述べたように周りの分子の配置、およびその配置が注目する分子対の距離の変化にともないいかに変化するか、に依存する。 ここでは注目する分子対を AB とし、周りの分子は常に平衡における配置をとるものとして考えることにする。 これはいわば注目する分子対 AB をある距離はなして固定し、その他の分子をその周りで熱平衡に達するまで運動させ、その時 AB 間に働く力の平均値を求めることに相当する。 こうすると AB の分子間に働く力 \(F_\mrm{AB}(r)\) として
\begin{eqnarray} \langle F_\mrm{AB}(r) \rangle &=& \left \langle -\pdif{U(r)}{r} \right \rangle \nonumber \\ &=& k_\mrm{B} T \frac{\rmd \ln g_\mrm{AB}(r)}{\rmd r} \label{eq:4.3.1} \end{eqnarray}
|
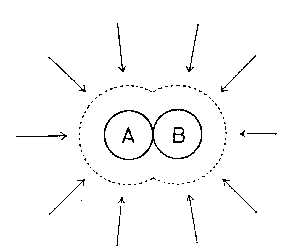
| 図 4.3. 分子対 AB に周囲から働く力 |
がえられる。[補注10] 図 4.2 から明らかに分子近傍では引力が働く。 これを概念的に説明するはきわめて簡単である。 図 4.3 に示すようにAB 両分子が接近して存在するときには、A から見て B の背後からあるいは B から見て A の背後から周りの分子が相互作用をおよぼす(=衝突する)かたちになる。 周りの分子は斥力的相互作用しか及ぼさないから、この配置での周りの分子からの作用は、AB 間の距離を押し縮めようとする向きに働くことは明らかであろう。 このような平均の力という立場からの剛体球流体の構造に対する理解は分子間距離が 0、つまり分子同士が重なり合うような場合に、有用で厳密な表現を与えることが知られている。 また分布関数の階級方程式はこのような視点から液体構造を眺めたことに相当すると考えることもできる。 しかし本研究ではこのような立場からの考察は以後行なわないのでこれ以上立ち入った議論はしないでおくことにする。
4.4 剛体球流体中における接触錯体生成にともなう体積変化
a.計算の方法
ここではいわゆる Carnahan-Starling 型の近似式[4.5]
\begin{equation} g(\sigma) = \frac{1}{3} g^\mrm{PY}(\sigma) + \frac{2}{3} g^\mrm{spt}(\sigma) \label{eq:4.4.1} \end{equation}
を用いることにする。 ここで、上つき PC は Percus-Yevick 方程式からの動径分布関数を spt は Scaled Particle 理論からの動径分布関数を示す。 この近似式は溶液についてもよく成り立つことが計算機シミュレ-ションによって確かめられており [4.6]、ここではそれを無限希釈状態にまで拡張する。 この式の利点は動径分布関数が解析的な形で与えられることで、溶媒の密度、溶媒・溶質分子のサイズの関数として次のように書き下すことができる。
\begin{equation} g_\mrm{AB}(\sigma_\mrm{AB}) = \frac{1}{1 - \eta} + \frac{3 \eta}{2 (1 - \eta)^2} \frac{\sigma}{\sigma_\mrm{S}} + \frac{\eta^2}{2 (1 - \eta)^3} \left( \frac{\sigma}{\sigma_\mrm{S}} \right)^2 \label{eq:4.4.2} \end{equation}
ここで、\(\sigma\) は考える溶質分子 A、B の直径から
\begin{equation} \sigma = \frac{2 \sigma_\mrm{A} \sigma_\mrm{B}}{\sigma_\mrm{A} + \sigma_\mrm{B}} \label{eq:4.4.3} \end{equation}
で定義される反応物のサイズ、\(\eta\) は溶媒のパッキング率で溶媒の数密度を \(n_\mrm{S}\) として
\begin{equation} \eta = \frac{\pi}{6} n_\mrm{S} \sigma_\mrm{S}^3 \label{eq:4.4.4} \end{equation}
つまり溶媒分子のコアの体積の総和と容器の体積の比である。
こうして、動径分布関数の表現が与えられれば、接触錯体生成の体積変化は次式に\eqref{eq:4.4.2} 式を入れることによってえることができる。
\begin{eqnarray} \Delta V &=& -\kappa_T k_\mrm{B} T - k_\mrm{B} T \pdif{\ln g_\mrm{AB}(\sigma_\mrm{AB})}{P} \nonumber \\ &=& -\kappa_T k_\mrm{B} T - k_\mrm{B} T \pdif{\eta}{P} \pdif{\ln g_\mrm{AB}(\sigma_\mrm{AB})}{\eta} \nonumber \\ &=& -\kappa_T k_\mrm{B} T \left[ 1 + \eta \pdif{\ln g_\mrm{AB}(\sigma_\mrm{AB})}{\eta} \right] \label{eq:4.4.5} \end{eqnarray}
ここで必要な圧縮率の値は\eqref{eq:4.4.3}式の動径分布関数の値を用いてビリアル式
\begin{equation} P = \frac{N k_\mrm{B} T}{V} [1 + 4 \eta g(\sigma_\mrm{S})] \label{eq:4.4.6} \end{equation}
によってえることができる。
b.接触錯体生成にともなう体積変化のふるまい
|
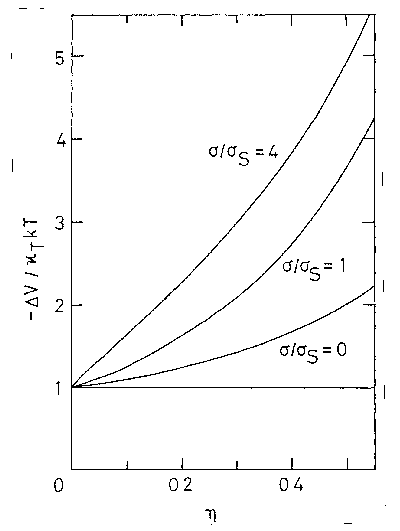
図 4.4. 接触錯体生成にともなう体積変化の密度依存性。図では並進の寄与で割った形で示してある。 |
aで計算の道具立ては整ったわけで、あと適当に条件を設定することにより、さまざまな条件下での接触錯体生成反応の体積変化を求めることができる。 まず、体積変化に占める並進、配置の寄与がパッキング率とともにどのように変化するかをみた。 図 4.4 には、体積変化を並進の寄与κTkT で割ったものをパッキング率に対して描いた。 図中のσ/σS = 0 の場合は3.5節で与えた剛体分子からなる流体中の質点の場合に相当し、 ちょうど質点の部分分子容をプロットしていることになっている。(質点同士の接触錯体の生成は、質点が融合して 2 分子が 1 分子になることに相当する)
予期される通り、希薄な領域で体積変化は並進の寄与で決まっている(図では 1 になる)が、パッキング率が上がり溶媒-溶質の相関が重要となるにしたがい、 配置の寄与が並進の寄与を上回るようになる(図では 2 以上になる)。 また反応物のサイズに注目すると、大きさを0からだんだん大きくしていくと溶媒のサイズ程度になるまで体積変化の大きさはかなり速く増大するがそれ以上になると、 体積変化のサイズ依存性は頭打ちになる傾向が認められる。 4.2 節の議論によれば、希薄気体中での体積変化は反応物の直径に比例して増大するはずであり、 多体的相互作用は反応物の個性を覆い隠す方向に働くようである。
|
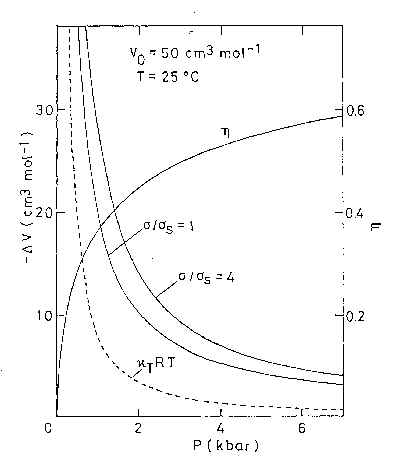
図 4.5. 接触錯体生成にともなう体積変化の圧力依存性。溶媒の分子コアを 50 cm3 mol-1、温度 25 °Cとしての計算。 |
次に現実の系との関連を見るため、温度を 25 °C で一定に保ち圧力を変化させたときの、体積変化の振舞いに注目する。 図 4.5 には、溶媒分子のコアの体積を 50 cm3 mol-1、 直径にすると \(\sigma_\mrm{S} = \mrm{0.54~pm\) とほぼ四塩化炭素程度の大きさにとった時の体積変化の挙動を示す。 圧力の増加とともに最初、体積変化の大きさは急速に減少し 2 kbar 程度からその減少の傾向は幾分弱まり漸減していく。 図では並進の寄与も含まれる結果配置の寄与の変化が見難い。 配置の寄与の大きさは図の場合、\(\sigma = \sigma_\mrm{S}\) の時、\(\eta\) が 0 の時 125 cm3 mol-1 であるのに対し、 \(\eta\) が 0.5 では 4.7 cm3 mol-1 にまでなる。 これは並進の寄与が無限大から 2.3 cm3 mol-1 になるのに比べれば小さい(このために高密度で配置の寄与が支配的な位置を占めるようになるともいえる)が、 ことが自らとの相関ではなく、異なる分子との相関であることを考えるときわめて大きな変化である。 このことは、3章で触れた多体的相互作用の重要さを如実に示しているといってよかろう。
c.実験値との比較
ここで取扱った接触錯体生成反応は現実の系でいえば電荷移動(EDA)錯体の生成反応と同様のものといえる。 すでに EDA 錯体生成の体積変化について多くの実験値が報告されている。 たいていの中性のEDA錯体については体積変化は負で - 5 cm3 mol-1 前後の値をとる。
実在の系と先ほどの剛体球系とを比較する際問題となるのは、実在の系の分子のサイズとりわけ溶媒分子のサイズをどの程度にとればよいかである。 これにはいくつかの見積もりの方法がある。四塩化炭素について次のような見積もりを行なってみる。
- 四塩化炭素の塩素・炭素各原子上にファンデルワ-ルス球を設定し、四塩化炭素のファンデルワ-ルス体積を求める。 得られたファンデルワ-ルス体積は 53.0 cm3 mol-1で 25 °C、1 atm でのパッキング率は 0.55。
- 四塩化炭素の\(\partial P/\partial T\) が\(P/T\)になるような剛体球流体のパッキング率: 0.51。
- 四塩化炭素の圧縮率を再現する剛体球流体のパッキング率: 0.45。
これらから、25 °C、1 atm の四塩化炭素液体に相当する剛体球流体のパッキング率は 0.50 であると見積られる。 これは、Chandler が粘性率から見積もった値 0.47 [4.7]とよく一致している。
こうして溶媒についての見積もりができたが、この値を用いて実際の系の体積変化の評価を行なう際には反応物の形・サイズをどのように考慮するかが問題となる。 簡単のためここでは、反応物のファンデルワ-ルス体積を計算しそれと等しい体積を有する球で反応物のサイズを評価し、形については不問に付すことにする。
| 反応系 | 溶媒 | 実測 | 計算 | 文献 |
|---|---|---|---|---|
| ベンゼン + TCNE | 四塩化炭素 | -3.4 | -6.4 | [4.8] |
| メシチレン + TCNE | 四塩化炭素 | -7.1 | -6.5 | [4.8] |
| ベンゼン + ヨウ素 | ヘキサン | -5.9 | -8.2 | [4.9] |
| a) ベンゼン、メシチレン、TCNE(テトラシアノエチレン)、ヨウ素の直径をそれぞれ 0.55、0.64、0.61、0.51 nm ととっての計算。 | ||||
表 4.1 に中山によって実測された TCNE-ベンゼンおよび TCNE-メシチレンの EDA 錯体生成の体積変化の値[4.8]と、 上のようにして評価した体積変化の値を示した。 分子の形を球に還元するなどの大担な近似を考えれば、実験結果との一致は良好である。 n-ヘキサン分子は大きく球形からはずれていると考えられる。 表にはまた、n-ヘキサン溶媒中におけるヨウ素-ベンゼン錯体の生成に対する体積変化に対する実験値[4.9]と計算値も示した。 ここでは n-ヘキサンのパッキング率をファンデルワ-ルス体積から見積って上と同様に計算してある。 これについても、計算値と実験値の一致はきわめてよい。
このような実験値と計算値の一致は体積変化の大きさのみでなく、体積変化の圧力依存性についても見ることができる。 体積変化の圧力依存性、\((\partial \Delta V/\partial P)\) の計算値は上で計算した四塩化炭素溶媒における接触錯体生成反応でおよそ 1.4 x 10-3 cm3 mol-1 bar-1 である。 これは多くの EDA 錯体生成反応について知られている体積変化の圧力依存性[4.10]とほぼ同程度である。
実験と計算の一致・不一致についてさらに反応物のサイズに対する依存性なども検討すべきであるが、現時点におけるさらに進んだ実験値と計算値との比較は、実験上の誤差が大きく不可能である。
第4章1、2節へ