|
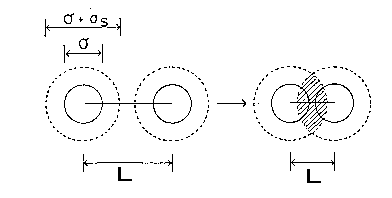
図 4.1. 剛体球分子(直径 \(\sigma_\mrm{S}\))からなる希薄気体中の剛体球分子(直径 \(\sigma\))同士の反応。 \(L\) が\(\sigma + \sigma_\mrm{S}\) よりも小さくなると、排除体積をあらわす球(図中の点線)同士の重なりがおこり、配置の体積変化が観測されるようになる。 |
前章で見たように、液体においては分子間力の斥力的な部分が最も重要な役割を担っている。 この章では斥力のみからなる系における体積変化の具体的な計算を通して、分子レベルの相互作用からみた体積変化の描像を明らかにする。
ここで取り扱うのは、溶液中に無限希釈量溶けている二個の分子が会合して一個の会合体分子を生成するという二分子会合反応である。
溶液中に A B 2個の球対称の分子が存在し、これが可逆的に会合するとしよう。 この反応系の全相互作用エネルギ-は対ポテンシャルエネルギ-の和となるものとし、溶媒-溶媒 \(u_\mrm{SS}\)、 溶媒-溶質 \(u_\mrm{SX}\) の相互作用としては溶媒が直径 \(\sigma_\mrm{S}\) 溶質が直径 \(\sigma_\mrm{X}\)(ここで、 X は A、B を指すものとする) であるような剛体球間の相互作用を想定する。 つまり
\begin{equation} u_\mrm{SS}(r) = \left \{ \begin{array}{l1} \infty & r \lt \sigma_\mrm{S}\\ 0 & r \ge \sigma_\mrm{S} \end{array} \right . \label{eq:4.1.1} \end{equation}
\begin{equation} u_\mrm{SX}(r) = \left \{ \begin{array}{l1} \infty & r \lt (\sigma_\mrm{S} + \sigma_\mrm{X})/2\\ 0 & r \ge (\sigma_\mrm{S} + \sigma_\mrm{X})/2 \end{array} \right . \label{eq:4.1.2} \end{equation}
のような相互作用を考える。
反応物 A 、B の間の相互作用はいわば反応座標に相当する。 これは反応のエネルギ-的な側面を考察するさいには重要だが、体積変化を取り扱う分には問題がないので、ここでは特別の指定を行なわない。 ただAB間の距離は体積変化を決める上の重要な要素でありこれを \(\lambda\) で示すことにする。 なお、これらすべてについて量子効果は無視でき古典的な取扱いができるものとする。
溶液反応の体積変化を具体的に議論する順序としてまず希薄気体における体積変化を取り上げることにしよう。 希薄気体では、溶質-溶媒の二体の相互作用のみが問題となり多体の相互作用は考える必要がなく、容易に厳密な結果を得ることができる。 これはまた溶媒-溶媒の相互作用を無視し、溶媒をあたかも連続体と見なすのと同等の扱いをしていることでもある。
希薄気体中での A B二体の動径分布関数は Mayer 関数 \(f_\mrm{AB}(r)\)
\begin{equation} f_\mrm{AB}(r) = \exp [-u_\mrm{AB}(r)/k_\mrm{B}T ] -1 \label{eq:4.2.1} \end{equation}
を用いた密度展開の第一項のみで近似できる[4.1]。
\begin{equation} \ln g_\mrm{AB}(r) = -u_\mrm{AB}(r)/k_\mrm{B} T + (\bigcirc_\mrm{A} — ⚫ — \bigcirc_\mrm{B}) n \label{eq:4.2.2} \end{equation}
ここで\(n\)は溶媒分子の数密度であり、グラフを結ぶ線分は \(f_\mrm{AS}(r)\), \(f_\mrm{AS}(r)\) にそれぞれ対応する。 場の点⚫ は溶媒 S についてのものでここでは添字を落としてある。 したがって、\(\Delta V\) は 2.2 節の議論から
\begin{equation} \Delta V = -\kappa_T k_\mrm{B} T \left[1 + (\bigcirc_\mrm{A} — ⚫ — \bigcirc_\mrm{B}) n \right] \label{eq:4.2.3} \end{equation}
ここで\(\kappa_T k_\mrm{B} T\)は、溶媒の第二ビリアル係数 \(B_\mrm{SS}\) を用いて次のようになる。[補注9]
\begin{equation} \kappa_T k_\mrm{B} T = \frac{V}{N} - 2B_\mrm{SS} \label{eq:4.2.4} \end{equation}
したがって、\(\Delta V\) は
\begin{equation} \Delta V = -\kappa_T k_\mrm{B} T - (\bigcirc_\mrm{A} — ⚫ — \bigcirc_\mrm{B}) \label{eq:4.2.5} \end{equation}
と書ける。 ここで、高次の項 \((\bigcirc_\mrm{A} — ⚫ — \bigcirc_\mrm{B}) B_\mrm{SS}\) は落とした。
この式は、希薄気体中の部分分子容の表現からも導くことができる。 希薄気体中における部分分子容は次の式で与えられる。
\begin{equation} V_\mrm{X} = \kappa_T k_\mrm{B} T + 2 B_\mrm{SX} \label{eq:4.2.6} \end{equation}
ところで、第二ビリアル係数はグラフを用いて
\begin{equation} B_\mrm{SX} = -\frac{1}{2} (\bigcirc_\mrm{X} — ⚫ ) \label{eq:4.2.7} \end{equation}
\begin{equation} B_\mrm{S(AB)} = -\frac{1}{2} \left[ (\bigcirc_\mrm{A} — ⚫) + (\bigcirc_\mrm{B} — ⚫) + (\bigcirc_\mrm{A} — ⚫ — \bigcirc_\mrm{B})) \right ] \label{eq:4.2.8} \end{equation}
のように書け、この差 \(2 [B_\mrm{S(AB)} - (B_\mrm{A} + B_\mrm{B})]\) は \eqref{eq:4.2.5} 式の第二項に一致する。
1章でみた表式に則ると、この体積変化中の第二項が反応物の個性を反映するはずであり、また実際そうなっている。 以下、この項に絞って議論を進めることにする。
\eqref{eq:4.2.5}式第二項には簡単で直接的な幾何学的意味を与えることができる。 扱いを簡単にし見通しをよくするため以下 A、B それぞれの直径は等しく \(\sigma\) であるとする。

|
図 4.1. 剛体球分子(直径 \(\sigma_\mrm{S}\))からなる希薄気体中の剛体球分子(直径 \(\sigma\))同士の反応。 \(L\) が\(\sigma + \sigma_\mrm{S}\) よりも小さくなると、排除体積をあらわす球(図中の点線)同士の重なりがおこり、配置の体積変化が観測されるようになる。 |
希薄気体中での化学反応にともなう体積変化は、並進の寄与の変化と第二ビリアル係数の変化の和であった。 ここで考えるモデルのように剛体的な相互作用からなる系では、第二ビリアル係数はちょうど排除体積の半分に等しい。 したがって、反応にともなう排除体積(図 4.1 の点線で囲まれた部分に相当する)の変化がまさに\eqref{eq:4.2.5}式の第二項なのである。 体積変化は反応の前後での排除体積の変化つまり、図 4.1 の斜線部分の体積に等しい。 \eqref{eq:4.2.5}式第二項のグラフの値はまさにこの部分の体積に一致する。 つまり観測される体積変化は、並進の寄与の変化としての \(-\kappa_T k_\mrm{B} T\) と排除体積の大きさに相当する球を水槽の中でくっつけた時に巨視的なレベルの操作で見出される体積変化との和なのである。
上のように問題は図の斜線の部分の体積の計算という幾何学的な問題に還元されたわけである。 実際にこれを計算すると
\begin{equation} \Delta V = \left \{ \begin{array}{c1} \displaystyle -\frac{\pi}{6} (\sigma + \sigma_\mrm{S})^3 + \frac{\pi}{4} (\sigma + \sigma_\mrm{S})^2 L - \frac{\pi}{12} L^3 & L \lt \sigma + \sigma_\mrm{S} \\ 0 & L \ge \sigma + \sigma_\mrm{S} \end{array} \right . \label{eq:4.2.9} \end{equation}
特に AB の結合距離が\(\sigma\)、すなわち A と B が接触しているときには
\begin{equation} \Delta V = -\frac{\pi}{6} {\sigma_\mrm{S}}^3 \left[ 1 + \frac{3 \sigma}{2 \sigma_\mrm{S}} \right] \label{eq:4.2.10} \end{equation}
という結果をえる。 これは大きく次の二つのことを告げてくれるものといえる。
まず第一に従来言われていた「固有の体積変化」なるものは、われわれの観測する体積変化をなんら説明するものではないということである。 これまで述べた並進の寄与については置くとして、配置の寄与のついてさえこれは正しい体積変化に対する描像を与えない。 とくに、単に二つの反応物が接触するのみで配置の体積変化が現れ観測にかかるということは従来の「固有の体積変化」のとうてい説明できるところではない。 さらに「固有の体積変化」に対する「補正項」としてこの不一致を処理しようにも、式の上での処理はかえって見通しを悪くし、はっきりした化学的な体積変化の描像を与えてくれるものではない。 従来の考えの不十分さとして、先に並進の寄与への配慮の欠如を挙げたが、従来の考えは配置の寄与についても有効たりえないのである。 これは、すでに3章でも述べたことであるが「固有の大きさ・ひろがり」というものはあくまでも紙の上の概念であって、 われわれが実際に観測する量でないことに照応している。
さらに、「固有の体積変化」という考えは体積変化を決める要因として溶媒の性質よりは反応物の性質の方に強く傾いた考えである。 ところが皮肉なことにここでえられた希薄気体中における体積変化の結果は反応物のサイズよりも溶媒のサイズに強く依存する。 A、B 2分子が接触している場合について(\eqref{eq:4.2.10}式)実際に計算してみよう。 たとえば、\(\sigma = \sigma_\mrm{S} = 0.2 ~\mrm{nm}\) とすると体積変化は -6.3 cm3 mol-1 である。 これから\(\sigma_\mrm{S}\) を大きくして 0.3 nm にとれば \(\Delta V\) は -18 cm3 mol-1 に、 一方 \(\sigma\) を大きくして 0.3 nm にとれば \(\Delta V\) は -8.2 cm3 mol-1 になる。 つまり溶媒の直径を5割増しすると体積変化が約3倍になるのに対し反応物の直径を同じく5割増ししても体積変化の大きさは3割程度増えるにすぎない。 従来の反応物に偏った見方の誤りは明らかである。
このように従来の見方が根本から誤っていたことが明らかになったわけだが、希薄気体特有の問題も見ておかねばならない。 体積変化についてえられた結果の内、配置の寄与の部分が液体における体積変化を占うことになるわけだが、それは普通の溶液反応で知られているものよりもはるかに絶対値として大きな値をとる。 またそれは大きなサイズに対する依存性を示す。 このことは液体における多体的相互作用が物質をより没個性的にふるまわせる方向に働くことをもの語る。