|
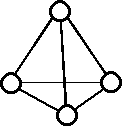
図 N7.1. こみ入った配置についての、生成物の同定。図で分子間の距離はいずれも \(r_0\) に等しく、4 分子は正四面体をなしている。 |
溶媒和の体積変化を想定する(あるいは想定できる)、背景には液体に対する摂動論的理解、つまり、ある参照系に対する摂動として溶媒和が扱えるとする考えがある。 一般に全系のハミルトニアン \(E\) が、参照系のエネルギ- \(E_0\) と摂動のエネルギ- \(V\) の和で
\begin{equation} E = E_0 + V \label{eq:N1.1} \end{equation}
と書けるなら、ヘルムホルツの自由エネルギ- \(A\) は、
\begin{equation} A = A_0 + V_0 - (\langle V^2 \rangle_0 - \langle V \rangle_0^2)/2 k_\mrm{B} T + \cdots \label{eq:N1.2} \end{equation}
と摂動展開することができる[A1.1]。 ここで \(\langle \rangle_0\) は参照系のカノニカル分布についての平均をあらわす。
一般に溶媒和として扱われる摂動は長距離におよぶものであるのに対し、参照系にとられる相互作用はきわめて近距離にしかおよばない。 したがってこの摂動項のみを問題にする限り参照系の波長の短い構造はほとんど見えてこない。 つまり摂動項のみを問題とする限り、参照系には届かないのである。 あるいは、摂動項、溶媒和の寄与のみを問題とする限りにおいては、真に困難な問題である参照系の性質の探求、 あるいは \eqref{eq:N1.2} 式のような問題の枠組自身をさして意識することなくやっていくことが可能なのである。 従来のいたずらに精緻な静電収縮理論に基づく議論の真の限界はここにあるといえよう。
なお、\eqref{eq:N1.2} 式から溶媒和についての議論も展開できるわけだが、本研究では参照系についての議論に絞り摂動については取扱わない。
ここでの溶媒分子間の相関からの寄与(→並進の寄与)がカノニカルな系においても現われることの証明は溶媒-溶質の相互作用のない場合に限られる。 カノニカルな系で部分分子容が並進と配置二つの寄与の単純な加算からなっていることはビリアル定理が保障してくれている。カノニカルな系ではビリアル定理
\begin{equation} PV = (N_1 + N_2)k_\mrm{B} T + (1/3) \sum_i \vec{F}_i \cdot \vec{r}_i \label{eq:N2.1} \end{equation}
が成立する。ここで \(\vec{F}_i\) は \(i\) 番目の粒子に働く力であり、\(\vec{r}_i\) はその位置ベクトルである。(ここで粒子の番号 \(i\) は粒子の種類を問わず付けられているものとする) この第一項が並進運動がある体積 \(V\) の中に限定されていることによることからくる項であり、第二項が粒子に働く相互作用に起因する項である。 この式から 2 の粒子の増加にともなう圧力の増加は
\begin{equation} \pdifA{P}{N_2}{T,V,N_1} = \frac{k_\mrm{B} T}{V} + \frac{1}{3V} \pdifA{\sum_i \vec{F}_i \cdot \vec{r}_i}{N_2}{T,V,N_1} \label{eq:N2.2} \end{equation}
で示される。 回りの分子と相互作用を持たないなら \eqref{eq:N1.2} 式の第二項は 0 であり本文中の結果を得ることになる。 結局ビリアル定理 \eqref{eq:N1.1} 式でビリアル \(PV\) が二つの項の単純な加算からなっていることが、部分分子容における単純な描像を可能にしているわけである。
従来、しばしばこのような項のことを「自由体積」などという概念に解消することが多かった。 この「自由体積」という概念は、ある分子が他の分子と衝突することなく運動しうる体積、というふうに解釈されていたように思われる。 今回えられた結果は、このような考えとは何の関わりも持たないことに注意されたい。 ここでいう並進の寄与は注目する分子と溶媒分子の間の相関によらず(つまり「注目する分子が自由に動き回れる体積」という概念とは無関係で)、 溶媒分子同士の相関にのみ依存するのである。
自由体積という概念は、今日的には、液体に対する細胞理論の所産として幾許かの有効性を持っているにすぎない。 この細胞理論の困難がはっきり指摘されたのは1950年のことであった(J. G. Kirkwood, J. Chem. Phys., 18, 380 (1950))。 その後も、その困難は解消されるようすがない。 この今日の時点においてこの自由体積を部分分子容にたいする理解に結び付ける論者は、まずなによりも自由体積という概念の有効性を今日的に組直すことから始めねばならないはずである。
液体・溶液の統計物理からの体積変化に対する理解の上で、歴史的にも、また分子間相互作用から部分分子容を考える基本的な枠組という点おいても、 溶液の示す熱力学諸量に関するBellとGattyの先駆的な業績 [1.1] は特に注目に値する。
奇しくも、ちょうど50年前、Evans と Polanyi の論文と同じく1935年に Bell と Gatty は分子的相互作用と溶液の熱力学諸量の関係を論じた論文を発表した。 彼らの議論によれば、溶質の熱力学的性質を決める溶質分子と他の物体との相互作用は次のように分けられる。
この構想の最も洞察に満ちた点は、注目する分子と容器の壁との相互作用の重要性に光を投げかけたことにある。 この相互作用により、分子の並進運動は容器内の空間に限定される。BellとGattyの指摘の画期的な点は、分子の並進運動の容器による限定を、"相互作用"というところで受けとめたところにある。 さらに、分子間の相互作用を斥力的部分と引力的部分に分けたことは、 0.1節で述べた旧来の体積変化の解釈における"分子それ自身"と"溶媒との相互作用"といったあいまいな概念規定を遥かに越えている。 この、BellとGattyの相互作用の捉え方は、後で述べる液体のファンデルワ-ルス描像を踏襲したものであるが、今日的な視点からみても妥当なものと認められる。(3章を見られたい) しかし何故か、このような枠組の有用性が明確に認識されることがなく、今日ではまったく忘れ去られているのは極めて遺憾な事態と言わざるをえない。 卒直に言って、もしこの枠組の上にその初期から溶液・液体の化学が組立てられていたなら、今日の体積変化の化学の貧困はなかったであろう。
このようにBellとGattyの業績は、分子の並進運動の寄与を正しく評価し問題の構造を明らかにするものではあったが、 真に困難な問題は溶質・溶媒間の相互作用と部分分子容との関係をどのように捉えるかにある。 実際、BellとGattyとてその論文の中で、溶質と容器との相互作用のみを問題とするところから、 分子間に斥力的相互作用の働く系の記述に踏込み始めたとたん、安易な自由体積理論に問題を解消しようとし始める。 この問題については3章で詳しく述べるが、自由体積なる概念を有効とするには、何らかの液体モデルの導入が必要である。 BellとGattyのように単なる化学ポテンシャルを求める分にはともかく、化学反応にともなう体積変化のようにモデル自身が変化を受ける現象については、 どうしてもモデルの構成に関わる任意性がつきまとうことになる。 このような任意性(恣意性)を避けるためにはどうしても分布関数と真正面からぶつかる必要がある。
部分分子容を語るにはこの密度-密度相関関数を知れば十分であった。 同様にわれわれの興味を持つ熱力学的特性は二量の間の相関関数に多く帰着される。 これは、われわれが物質を特徴付けるのに用いる熱力学量の多くが、結局のところ応答関数であることによっている。 熱ようどう理論によって応答関数は、対象とする系の応答を観測される熱力学量と、外部から加わる力に共役な熱力学量の間のゆらぎに関係付けられる。 つまり、二量の間の相関に帰着するわけである。 このことはまた、二量の相関関数に対する関心が何故に高くならねばならないかの根拠でもある。
密度-密度相関関数は、われわれの観測する熱力学量から出発するような分布関数であるが、 いわゆる二体の分布関数 \(n_{ij}(r,r')\)はある体系が与えられたとき、\(i,j\)に属する粒子間の相関を示すものであり、 2.1 節の密度-密度分布関数の第一項に相当する。 ただし系内から2個の粒子を弁別してその間の相関をみるという立場に立つため、 密度-密度相関関数の取扱いとは \(i = j\) つまり同じ分子種の間の相関をみるときにいくぶんの食い違いが生まれる。 密度-密度相関関数の場合にはアンサンブルについての平均をとるさいに、自分自身に対する相関もとることになる。 つまり、密度-密度相関関数の場合には同一種類の相関を扱う際距離 0 の所に非常に大きな相関があらわれる。 これに対し二体分布関数の場合にはこのようなアンサンブルは平均化操作に加えない。 これは離れた地点の間の値をみる分に問題はないが2.1 節のようにある空間全体について積分をほどこすような場合にはこの差異がちょうど粒子数分だけきくことになる。 これは考えるゆらぎと同じ程度の大きさで無視できない寄与をすることになる。 しかし、本研究においてはこの種の問題には特に触れないのでこれ以上論じることはしない。
生成物分子を数え上げる際には注意すべき問題が大きく二つある。 一つは重なって数えてしまうことで、2.2 節において \(c_1! c_2! \cdots\) で割っているのは、 分布関数 \( n(\vec{r}_1, \vec{r}_2, \cdots)\) においてはアンサンブル平均をとる際に同じ粒子が同一の地点にあるようなアンサンブルも平均化操作に含めているためである。 たとえば同じ種類の分子について二体の場合に考えてみよう。 今 AB 両地点に粒子の存在する確率を取り上げた際、あるアンサンブルでは A に番号 1 の粒子が B に番号 2 の粒子が存在し、 またあるアンサンブルでは A に 2 が B に 1 が存在するものとしよう。 こうしたとき、単に存在する確率を考える分には両者は同一の重みで寄与することになり、両者ともに考慮される。 しかし、粒子対を数え上げる立場から言えば、この二つのアンサンブルを重ね合せれば 1 という粒子が A と B 両地点に同時に存在する場合を考慮していることになっている。 このようなアンサンブルの数はちょうど 2! 個あるわけで粒子対を数え上げるためには、これで分布関数を考えるときに用いたアンサンブルの数を割っておく必要が生じる。

|
図 N7.1. こみ入った配置についての、生成物の同定。図で分子間の距離はいずれも \(r_0\) に等しく、4 分子は正四面体をなしている。 |
次に問題になるのは、入り組んだ配置についての生成物の数え上げの問題である。 たとえば、2.2 節で考えた二量化の場合、今回のように二体の分布関数から生成物の総量を決定すれば、 図 N7.1 のような場合単に距離が \(r_0\) であるからという理由で生成する二量体分子 Y は 6 分子存在すると認定することになる。 これは2分子が会合して 4 分子から 6 分子できたことに相当するわけで化学量論からは首肯しがたい結果といえよう。 この困難は基本的には、いかにわれわれが Y と認定するかという問題に深く関わることになる。 ただしこれらの複雑な配置からの寄与は注目する配置よりもより多い数の分子の配置を対象にするわけで (たとえば図の場合なら、二体の配置に注目するときに四体の配置のある特定のものに注目していることになる)、 本研究でもっぱら考える無限希釈状態では無視できる。 一般の場合については、まだ深く考えねばならない。
このように、2、3次元の問題では各アンサンブルでの面積・体積を系統的に正確に求めることが極めて困難であるが1次元の場合にはこれが可能であることが示されている。 (L. Tonks, Phys. Rev., 50, 955 (1936)) ここから得られる部分分子容(部分分子長さ)についての、1次元の系の性質は以下のとおりである。
1次元剛体棒分子系の状態方程式は、系の長さを \(L\)、分子の長さを \(\lambda\) として
\begin{equation} L = Nk_\mrm{B}T/P + N \lambda \label{eq:N8.1} \end{equation}
となる。 これを 1, 2 の二成分系に拡張し、今回もっぱら考える 2 が無限希釈量の場合について 2 の部分分子長さ \(\bar{L}_2\) は
\begin{eqnarray} \bar{L}_2 &=& \kappa_T k_\mrm{B} T + \bar{L}_2(\mbox{配置}) \nonumber \\ &=& \frac{(\bar{L}_1 - \lambda_1)^2}{\bar{L}_1} + \lambda_2 + \frac{\lambda_1 (\bar{L}_1 - \lambda_1)}{\bar{L}_1} \label{eq:N8.2} \end{eqnarray}
となる。 ここで \(\bar{L}_1\) は溶媒 1 の部分分子長さ(\(= L/N_1\)、\(\lambda_1\) は溶媒の、\(\lambda_2\) は溶質 2 の分子コアの長さであり、 第一項が並進の寄与 \(\kappa_T k_\mrm{B} T\) に、第二項以下が配置の寄与にそれぞれ対応している。 部分分子長さに対する配置の寄与に注目すると、これは注目する分子 2 の分子コアの長さと溶媒分子のコアの長さで決まる項の和になっている。 つまり、1次元剛体棒系においては、分子コアが \(\delta \lambda\) 増せば、部分分子長さも同じく \(\delta \lambda\) 増すことになる。 これは巨視的物体の測定の場合とよく似ている。 ただし、分子コアが 2 倍になったからといって部分分子長さが 2 倍になるほど単純ではないが...
一成分の希薄気体の圧縮率の表現は状態方程式から出発して以下のように導かれる。
\begin{equation} P = nk_\mrm{B}T (1 + Bn) \label{eq:N9.1} \end{equation}
ここで \(B\) は第二ビリアル係数、\(n\) は分子の数密度である。
\begin{eqnarray} \kappa_T &=& \frac{1}{n} \pdif{n}{P} \nonumber \\ &=& \frac{1}{nk_\mrm{B}T (1 + 2Bn)} \label{eq:N9.2} \end{eqnarray}
ここで \(Bn\) が 1 より十分小さいはずだから
\begin{equation} \kappa_T = \frac{1 -2Bn}{nk_\mrm{B}T} \label{eq:N9.3} \end{equation}
これを部分分子容に対する並進の寄与の形に書けば
\begin{equation} \kappa_T k_\mrm{B}T = n^{-1} -2B \label{eq:N9.4} \end{equation}
という式をえる。 これはまさに 4.2a 節で見たものである。
2 個の分子 A、B を距離 \(r\) 離して置いたとき、その間に働く力 \(F_\mrm{AB}(r)\) の平均値は
\begin{equation} \langle F_\mrm{AB}(r) \rangle = \frac{\langle -(\partial U(r)/\partial r) \exp[-U(r)/k_\mrm{B}T] \rangle}{\langle \exp[-U(r)/k_\mrm{B}T] \rangle} \label{eq:N10.1} \end{equation}
で与えられる。 ここで \(U(r)\) は AB 間の距離を \(r\) にしたときの全ポテンシャルエネルギ-である。 一方、動径分布関数は
\begin{equation} g_\mrm{AB}(r) = \frac{\langle \exp[-U(r)/k_\mrm{B}T] \rangle}{\langle \exp[-U/k_\mrm{B}T] \rangle} \label{eq:N10.2} \end{equation}
で表わされる。 ここで \(U\) は AB 間の距離に制限を設けない全ポテンシャルエネルギ-である。 したがって、\eqref{eq:N10.2} 式の対数をとり \(r\) について微分すれば \eqref{eq:N10.1} 式、つまり平均の力を得ることができる。
5.1 節の Traube の加成則から明らかに、化学反応の結果分子数が1だけ減るならば原子数は変化しないから、 体積変化の大きさは反応物の個性によらず一定で共通体積 \(\mathit{\Phi}\) に等しくなる。 このことは Traube 自身によって指摘されたところでもある。(J. Traube, “Ausdehnung der Gesetze von Gay-Lusaac und Avogadro auf homogene Fluessigkeiten und feste Stoffe,” Ber., 28, 3292 (1895).) この論文の題名にも明らかなとおり Traube は気体反応の法則との関連をこの事実にみた。 しかし、このような議論は1章でも見たように気相では部分分子容に対する並進の寄与が、また液相では配置の寄与が支配的に働くのであり安直な関連付けは誤りである。 しかし、その理論的な妥当性はともかく5.1 節の式で多くの物質の部分分子容がおおよそ表現されるとするなら、 これは真険に考えねばならない結果といえる。 本研究では6章でこれに関連する立場から、部分分子容の組立てを論じることになる。