|
図6.1 n-アルカン分子のコアのモデル。 |
これまで化学反応にともなう体積変化が物理化学の立場から正面きって議論されることの少なかった背景には 「体積変化は、所詮、反応前後の部分分子容の差にすぎない。」という体積変化を落としめた認識があったように思われる。 このような見地から見るかぎり体積変化の化学は部分分子容の化学の侍女にすぎず、体積変化の化学に対する活発なアプロ-チの生まれようもない。 たしかに、体積変化は部分分子容の反応前後の差以上のものではなかろう。 しかし、部分分子容がいったい何ものであったのだろう。むしろ問題はそこにある。
5章で部分分子容の化学の従来の枠組における主要な武器であった部分分子容の加成則を詳細に検討した。 加成則は分子各部からの部分分子容への寄与がそれぞれ独立に決まることを保障する。 検討した n-アルカンについてこの成立は見事であった。 しかし、その分子各部の部分分子容への寄与のしかた、その部位のコアの大きさが部分分子容にいかにあらわれるか、にはその分子各部の“かたち”が鋭く反映していた。
この分子各部の部分分子容への寄与のしかたの相違について、5章では分子各部の幾何学的な特性、コアの体積と面積の比、に帰着させて解釈を行なった。 このような解釈は分子コアを総体として扱おうとする行き方である。 しかし、分子コアの各部の示す性質が異なる以上、それをいくつかの構成単位に分割して取り扱う行き方、分割と結合という立場からこれを見直すアプロ-チはごく自然な行き方といえよう。 この分割と結合という操作に、化学反応という概念が結びつく。 実際、部分分子容の加成則はある分子に1つ構成単位を付加したさいの部分分子容の増分が一定であることを意味している。 これと同様に液体論においても、形を持った分子についてそれをそのまま総体として扱う行き方[6.1]と、 いくつかの相互作用のサイトの集まりとして扱う行き方[6.2]として行なわれている。 化学反応から部分分子容を見る立場は、この後者の立場に相当する。 この章では化学反応にともなう体積変化の立場から部分分子容の加成則を見直しその新たな意味を検討する。
序言で述べたように体積変化は部分分子容がわかればわかるという関係にある。 しかし、問題は「部分分子容がわかる」とはどういうことかにある。
部分分子容を理解するさまざまな立場がある。 中で最も代表的なものは加成則に代表されるように分子の構成単位からどのように部分分子容が組立てられているかを記述する立場である。 構成単位 \(\mrm{A_1}\)、\(\mrm{A_2}\)、\(\mrm{A_3}\) ・・・ のそれぞれ \(c_1\)、\(c_2\)、\(c_3\) ・・・ 個からなる複合分子 \(\mrm{A}\) を考えよう。 この立場はこの分子の示す性質 \(X(\mrm{A})\) を次のように書き下すことに相当する。
\begin{equation} X(\mrm{A}) = [c_1 X(\mrm{A_1}) + c_2 X(\mrm{A_2}) + c_3 X(\mrm{A_3}) + \cdots] + \Delta X(\mrm{A}) \label{eq:6.1.1} \end{equation}
つまり、この式の第一項は構成単位の間に何らの関係のない場合の性質であり、複合分子の性質は第二項の\(\Delta X(\mrm{A})\) に現われるわけである。 第一項は分子式に対応し第二項はその間の関係、構造を示しているともいえよう。 たとえば C3H6 という分子式で示される化合物 A を考えよう。 この分子の示す性質 \(X(\mrm{A})\) は、
\begin{equation} X(\mrm{A}) = [3 X(\mrm{C}) + 6 X(\mrm{H})] + \Delta X(\mrm{A}) \label{eq:6.1.2} \end{equation}
と書ける。 C3H6 という分子式で表わされる物質としては、プロピレンとシクロプロパンという二つが考えられる。 性質 \(X\) についての二つの物質の差異はこの\(\Delta X(\mrm{A})\) の中にすべて含まれているわけである。
今日もっぱらわれわれが関心を抱くのは、分子の構成単位の数ではなく分子がその構成単位からいかに組立てられているかである。 こうしたとき\eqref{eq:6.1.1} 式の視点は、A の性質を知ること「わかること」がすなわち A が構成単位から組立てられる際の変化を知ることであることを告げる。 \(X\) を部分分子容と読みかえれば、ある物質の部分分子容を知ること「わかること」はすなわちその物質がその構成要素から組立てられる際の体積変化を知ることにほかならないのである。
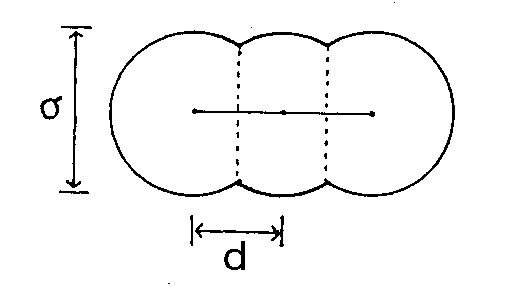
5章で n-アルカン分子のモデルを与えた。 ここでは、n-アルカン分子を作っていく過程に強く関わる形で、溶液・液体に対するファンデルワ-ルス描像に従い次のようなモデルを導入する。

|
図6.1 n-アルカン分子のコアのモデル。 |
アルカン分子はその炭素数 \(n\) と同じ個数の球対称の構成単位 M からできているものとみなす。 この構成単位 M は溶媒分子とは直径 \(\sigma\) の剛体球としてふるまい、図 6.1に示すように分子軸上に等間隔 \(d\) で配置するものとする。 これに従えば、メチレン基は2個の M と隣り合っている構成単位 M のことであるし、メチル基は1個の M と隣り合っているもののことということになる。
なお溶媒分子も構成単位 M と同じく剛体球とし、その直径を \(\sigma_\mrm{S}\) とする。
前節でのべたアルカン分子のモデルについて \eqref{eq:6.1.1} 式を適用すれば、\(n\) 個の炭素原子を含むアルカンの場合、その部分分子容は次のようになる。
\begin{equation} \bar{V}(n) = n v + \Delta V(n) \label{eq:6.3.1} \end{equation}
ここで、\(v\) は M 単独での部分分子容である。 これに対して加成則が成立するためには \(\Delta V(n)\) が次の要件を満たす必要がある。
\begin{equation} \Delta V(0) = 0 \label{eq:6.3.2} \end{equation} \begin{equation} \Delta V(n) = \Delta V(n-1) + \Delta v \label{eq:6.3.3} \end{equation}
ここで \(\Delta v\) は、\(n\) によらない定数である。 これから、
\begin{equation} \Delta V(n) = (n - 1) \Delta v \label{eq:6.3.4} \end{equation}
でなければならない。 これには次のような、重合反応の一連の過程を考えることによってもう少しはっきりした意味付けができる。
| ○ + ○ → ○○ | \(\Delta v_2\) |
| ○○ + ○ → ○○○ | \(\Delta v_2\) |
| ・・・ | |
| ○○・・○ + ○ → ○○・・○○ | \(\Delta v_n\) |
この一連の反応の各段階の体積変化 \(\Delta v_2\)、\(\Delta v_3\)、・・・ 、\(\Delta v_n\) がすべて \(\Delta v\) に等しい、という主張がすなわち \eqref{eq:6.3.4} 式の言うところである。 この主張を「単位反応の体積変化の独立性の仮定」と呼ぶことにする。
この立場から、部分分子容の加成則を整理すると、
\begin{eqnarray} \bar{V} &=& n v + (n-1) \Delta v \label{eq:6.3.5} \\ &=& (v + \Delta v) n - \Delta v \label{eq:6.3.6} \end{eqnarray}
より、5.2 節で見た n-アルカンの加成則の表現では
\begin{equation} \alpha = v + \Delta v \label{eq:6.3.7} \end{equation} \begin{equation} \beta = -\Delta v \label{eq:6.3.8} \end{equation}
ということになる。 以下、この表現を用いて加成則と体積変化との関わりを議論していくことにする。 その上で並進の寄与を逐一考えていくのは面倒なので、以下の議論では \(\beta\) から並進の寄与 \(\kappa_T k_\mrm{B} T\) を落としたものを同じく \(\beta\) と書いて議論することにする。 同じ記号を用いるので注意されたい。
なお、5章で用いたモデルからは \(\bar{V}\) は
\begin{equation} \bar{V} = \kappa_T k_\mrm{B} T + (n - 1) V(\mbox{単位シリンダー}) + 2V(\mbox{半球}) \label{eq:6.3.9} \end{equation}
となるわけだが、今回の体積変化からの描像にしたがえば単位シリンダ-(長さが \(d\)で、半径が \(r\) の円柱)あたりの部分分子容への寄与 \(V(\mbox{単位シリンダー})\) および半球部分の寄与 \(V(\mbox{半球})\) はそれぞれ
\begin{equation} V(\mbox{単位シリンダー}) = v + \Delta v \label{eq:6.3.10} \end{equation} \begin{equation} V(\mbox{半球}) = [v - \kappa_T k_\mrm{B} T]/2 \label{eq:6.3.11} \end{equation}
ということになる。 つまり5章でみた半球部分とシリンダ-部分との差は、 アルカンの構成単位M単独での部分分子容に対する配置の寄与と、それに体積変化に対する配置の寄与を加えたものとの差に相当するわけである。