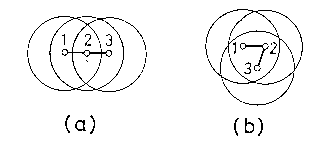
|
図 6.2. 希薄気体中における3分子会合。 最近接分子間(1-2、2-3)の距離 \(d\) は等しく、 図中の円はそれぞれ、溶媒分子に対する排除体積に相当する。 |
前節でみた体積変化の独立性の仮定は次のような操作を分布関数に対して施していることに対応する。 一般に前節で考えた体積変化 \(\Delta V(n)\) は \(n\) 体の分布関数を用いて次のように書ける。
\begin{equation} \Delta V(n) = -(n-1) \kappa_T k_\mrm{B}T - k_\mrm{B}T \pdif{\ln g(r_1, r_2, \ldots, r_n)}{P} \label{eq:6.4.1} \end{equation}
先の体積変化の独立性の仮定は、これを次のように書いたことになっている。
\begin{equation} \Delta V(n) = -(n-1) \kappa_T k_\mrm{B}T - (n-1) k_\mrm{B}T \pdif{\ln g(d)}{P} \label{eq:6.4.2} \end{equation}
つまり \(n\) 体の分布関数 \(g(r_1, r_2, \ldots, r_n)\) が2体の分布関数 \(g(r)\) によって
\begin{equation} g(r_1, r_2, \ldots, r_n) = \prod g(r_\mrm{np}) \label{eq:6.4.3} \end{equation}
のように書けることを主張するわけである。 ここで、np は最近接の M-M の対を、\(r_\mrm{np}\) はその距離を示す。 従来多体の分布関数については Kirkwood の重ね合せ近似が広く用いられてきた[0.7]。 Kirkwood の重ね合せ近似においては最近接の対のみならずすべての対についての2体の分布関数の積がとられる。 体積変化の独立性の仮定、あるいは部分分子容の加成則はこの Kirkwood の重ね合せ近似が、分子間の相関を過大に評価していることを告げる。
実際、Kirkwood の重ね合せ近似は対象とする分子配置で分子が余りに近接するときには破綻するはずのものである。 このことは3分子の M が反応して、3分子がちょうど重なりあい1分子の M となる(つまり \(d = 0\))という極端な場合を考えることによってあからさまな形で示すことができる。 明らかに、この反応の体積変化は \(-2v\) に等しい。しかし、Kirkwood の重ね合せ近似はこの反応に対して
\begin{eqnarray} \Delta V(n) &=& -2 \kappa_T k_\mrm{B}T - k_\mrm{B}T \pdif{\ln [g(r_12) g(r_23) g(r_31)]}{P} \\ &=& -2 \kappa_T k_\mrm{B}T - 3 k_\mrm{B}T \pdif{\ln g(0)]}{P} \\ &=& \kappa_T k_\mrm{B}T - 3 v \label{eq:6.4.6} \end{eqnarray}
のように正しい結果を与えない。 なおここで、\(r_{ij}\) は反応する M 分子に 1, 2, 3 の番号をつけたときの \(i, j\) 番目の分子の間の距離である。 この一方、体積変化の独立性の仮定・部分分子容の加成則からの要請としての \eqref{eq:6.4.3} 式は正しい結果 \(-2v\) を与える。
前節の最後の部分で、体積変化の独立性の仮定が反応分子が重なり合う極端な場合について成り立つことをみた。 しかし、加成則が環状アルカンに対してやぶれるように、生成する分子の配置によってはこの仮定の成立しない場合があるはずである。 高密度流体中における体積変化の取り扱いは実際的に不可能なので、この節では厳密な議論が可能な希薄気体中における体積変化についてこの仮定の妥当性を検討する。
4章で議論したように、希薄気体中における剛体的相互作用をする物体の化学反応にともなう配置の体積変化は、その排除体積の変化という幾何学的な問題に還元される。 図 6.2 に 1、2、3 という3分子が会合するときのようすを示した。 ここでそれぞれの球の排除体積を 1、2、3 という数字で示すことにして、球の重なりの体積をたとえば 1 と 2 の球との重なりならば \(1 \cap 2\) などと書くことにする。 4章で述べたように、この \(1 \cap 2\) は 1 と 2 の間の動径分布関数の対数の密度展開の第一項であり、希薄気体においてはちょうど動径分布関数の対数であるかのように扱えることに注意されたい。
上のような記方に従うと、3分子の会合にともなう体積変化は次のように書ける。
\begin{equation} \Delta V(\mbox{配置}) = - [1 \cap 2 + 2 \cap 3 + 3 \cap 1] + 1 \cap 2 \cap 3 \label{eq:6.5.1} \end{equation}
多体の分布関数を2体の分布関数に引き直す上では、この式の第二項をいかに取扱うかが問題となる。 体積変化の独立性の仮定はここで
\begin{equation} 3 \cap 1 = 1 \cap 2 \cap 3 \label{eq:6.5.2} \end{equation}
とおくことに相当し Kirkwood の重ね合せ近似は \eqref{eq:6.5.1} 式の第二項を無視することになっている。 このような近似がそれぞれどのような場合に妥当するかを検討してみることにしよう。
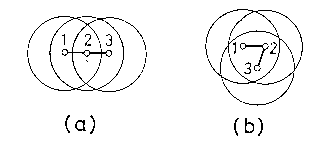
|
図 6.2. 希薄気体中における3分子会合。 最近接分子間(1-2、2-3)の距離 \(d\) は等しく、 図中の円はそれぞれ、溶媒分子に対する排除体積に相当する。 |
まず、体積変化の独立性の仮定の妥当性について見てみよう。 図 6.2a の場合には、\eqref{eq:6.5.2} 式が成立し体積変化が独立になるが、 折線型の 図6.2b で折線のなす角度が \(2 \cos^{-1} [d/(\sigma + \sigma_\mrm{S})]\) よりも小さいときには成立せず体積変化はもはや独立ではない。 したがって体積変化が独立であるためには、できた会合体が直線に近いことが必要であることが結論される。 これから、アルカンでも入り組んだ構造を持つものについては加成則が成立しないことが予見できる。 実際、環状アルカンでは小員環について加成則が成立しないし、枝分かれのあるアルカンについて加成則からのはずれをいかに評価するかは古くから加成則を語る上での重要なテ-マであった。
Kirkwood の重ね合せ近似は3個の球が同時に重なる限り、必ず分布関数を過大に評価する。 つまりKirkwood の重ね合せ近似は、3個の分子が互いに離れているときに妥当するのであって、 3個の分子が互いに近接する場合、とりわけ化合物を作り互いに入組んだ配置をとるような場合には破綻するであろうことがわかる。
ここで議論したのは溶媒の密度のきわめて低い状態の場合についてのものである。 密度が高くなれば離れたサイトの間にも相関が生まれここでのような単純な議論は妥当しない。 しかし、5章でみたように、アルカンの加成則は無限希釈条件下できわめて安定に成り立つ法則である。 多体的な相互作用が存在して、なおかつ体積変化の独立が成り立つことを示すにはもっと進んだ議論がまたれる。 (Kirkwood の重ね合せ近似の改良の試みとしてたとえば[4.3]がある)
前節までの議論で、加成則が体積変化の計算を2体の問題に還元することをみた。 この節では、実際にアルカンのモデルに基づいて加成則の係数を定め、その振舞いを検討する。
実際の計算においては、2体の空孔分布関数を何らかの方法で正しく評価する必要がある。 以下の計算では、空孔分布関数が
\begin{equation} \ln y(r) = a_0 + a_1 (r/\sigma) + a_3 (r/\sigma)^3 \label{eq:6.6.1} \end{equation}
の3次式で表現されるものとし、それぞれの係数を適当に定めることによって空孔分布関数を評価した。 (付録5を見よ) ここで、\eqref{eq:6.6.1} 式の係数は、溶媒の密度のみの関数であることに注意されたい。
空孔分布関数の具体的な評価ができれば、6.3 節の所論に基づいて体積変化 \(\Delta v\) と構成単位単独での部分分子容 \(v\) の値から\(\alpha\)、\(\beta\) の評価を行なうことができる。 ここでは\(\alpha\)、\(\beta\) の密度およびサイズ依存性を検討する。 なお、溶媒の密度については4章で用いたパッキング率 \(\eta\)、また \(\alpha\)、\(\beta\) についてはそれぞれ M のコアの体積で割った
\begin{equation} \alpha_\mrm{r} = \alpha/[(\pi/6) \sigma^3] \label{eq:6.6.2} \end{equation} \begin{equation} \beta_\mrm{r} = \beta/[(\pi/6) \sigma^3] \label{eq:6.6.3} \end{equation}
という還元量を用いることにする。
|
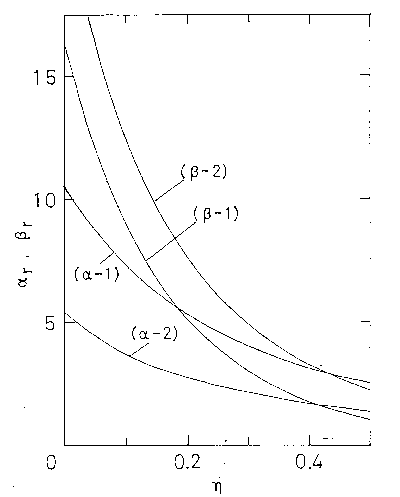
図 6.3. 結合距離 \(d\) を \(0.8 \sigma\)、\(0.4 \sigma\) にとったときの \(\alpha\) および \(\beta\) の溶媒のパッキング率依存性。 \((\alpha-1)\) と \((\beta-1)\) は \(d = 0.8 \sigma\)、\((\alpha-2)\) と \((\beta-2)\) は \(d = 0.4 \sigma\) についての計算値。 なお、\(\sigma/\sigma_\mrm{S}\) はいずれにおいても 0.5 にとっている。 |
図 6.3 には \(\alpha\) と \(\beta\) の密度依存性を示す。 図では、構成単位の直径を溶媒分子の半分にとっている。 密度の増大とともに \(\alpha\)、\(\beta\) は急速に減少していく。 この両者の減少の度合を比較してみよう。 結合距離が \(0.4\sigma\) の場合 \(\beta\) と \(\alpha\) の比は \(\eta\) が 0(希薄気体の場合に対応する)、0.2、0.4と増大するとき、4.03、2.82、1.96と減少する。 明らかに \(\beta\) の方が \(\alpha\) に比べて大きな密度依存性を示すことがわかる。 このことは、5章でみた実験事実と一致する。 \(\beta\) の方が \(\alpha\) に比べて大きな密度依存性を示すということは見方をかえれば、 希薄気体におけるメチル基部分とメチレン基部分のパッキングの大きな差異が密度を高めるにしたがって減少していくことを意味する。 つまり多体的な相互作用はより均一なパッキングをもたらすのである。 (希薄気体中の挙動については付録4を参照されたい)
|
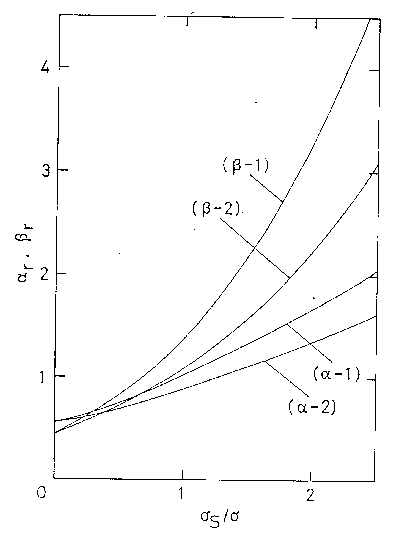
図 6.4. \(\alpha\) および \(\beta\) のアルカン構成単位のサイズに対する依存性。 \((\alpha-1)\) と \((\beta-1)\) は \(\eta = 0.4\) に、\((\alpha-1)\) と \((\beta-1)\) は \(\eta = 0.5\) についての計算値。 なお結合距離 \(d\) は \(0.4 \sigma\)ととってある。 |
図 6.4 は、\(\alpha\) と \(\beta\) の溶媒分子のサイズに対する依存性を示す。 この図では、構成単位間の結合距離を \(0.4 \sigma\)にとってある。 溶媒のサイズが大きくなるに従い、\(\alpha\) と \(\beta\) はともに増大する。 そして \(\alpha\)、\(\beta\) ともに溶媒の密度の増加により急速に溶媒分子のサイズに対する依存性を失っていく。 また \(\alpha\) と \(\beta\) ともに密度が高くなるにしたがい、急速にサイズ依存性を失っていくことがわかる。
パッキング率を一定にした条件下で \(\alpha\)、\(\beta\) に対する溶媒効果をみると、\(\eta = 0\) のときには \(\sigma_\mrm{S}\) を 0 (つまり、溶媒を連続体とみなしたとき)から 1 にすることによって、\(\alpha\)、\(\beta\) がそれぞれ 4.17、13.0 倍になるのに対し、 \(\eta = 0.2\) のときには 2.54、5.78 倍、さらに \(\eta = 0.4\) では 1.81、3.16 倍に止まる。 多体的相互作用は、溶媒の個性を覆いかくす方向に働くとみてよいようである。 また \(\alpha\) と \(\beta\) の間の溶媒依存性をみると密度依存性と同じく、やはり \(\beta\) の方が大きな依存性を示す。 この結果前節で見たように、希薄気体においては \(\beta\) の方が \(\alpha\) に比してきわめて大きな溶媒サイズ依存性を示すわけだが、 密度が高くなるにしたがいこの両者の溶媒分子のサイズへの依存性の差は小さくなっていくのである。 なお、この図 6.4 からは一見すると、構成単位のサイズが大きくなると、 \(\alpha\)、\(\beta\) が減少するように見える。 \(\alpha\)、\(\beta\) の大きさ自身は\(\sigma_\mrm{S}\) を一定にして構成単位の直径を大きくすれば、大きくなるが、 その大きくなり方が構成単位のコアの体積変化の増加よりも小さい。 このため、図では \eqref{eq:6.5.2}、\eqref{eq:6.5.3} 式で表わされるような還元された量を取っているので、図のようにあたかも \(\alpha\)、\(\beta\) が減少するような挙動が見えるのである。
このように、密度を高くすることによって溶媒のサイズに対する依存性、密度に対する依存性が減少し、 それらはまた5章でみた分子各部のパッキング率の差異を減少させる方向に作用することが明らかとなった。 これは密度が高くなるにつれ、あたかも溶媒が連続体であるかのように扱えることを意味する。 従来、溶媒を連続体として取扱ってさほど大きな破綻の現われない場合のあったことはこのことに基づいているのであろう。
えられた空孔分布関数についての表現を用いて、アルカンの構成単位として用いた球の直径 \(\sigma\) と結合距離 \(d\) を求めてみよう。 四塩化炭素溶媒中でアルカンの部分分子容についての加成則から実験的に
\begin{equation} \alpha = 16.48~\mrm{cm^3~mol^{-1}} \label{eq:6.6.4} \end{equation} \begin{equation} \beta = 30.7~\mrm{cm^3~mol^{-1}} \label{eq:6.6.5} \end{equation}
であることがわかっている。 6.3 節 の議論から \(v\) と \(\Delta v\) は容易にえられ、この \(v\) を再現する \(\sigma\) を求め、その後 \(\Delta v\) を再現する \(d\) を求めるという手順で、 \(\sigma\)、\(d\) を決める。 計算にあたってはまず、四塩化炭素溶媒に相当する剛体球流体を特徴付けるパラメ-タ-(剛体球直径 \(\sigma_\mrm{S}\) とパッキング率 \(\eta\))を決めなければならない。 ここでは、4章と同じ値を採用する。 さらに、必要な溶媒の圧縮率、圧力は先の空孔分布関数とビリアル定理から算出されるものを用いた。 このような道具立てが整うと、最適の \(\sigma\)、\(d\) を求める計算は逐次近似法を用いて容易に行なうことができる。 えられた \(\sigma\)、\(d\) はそれぞれ
\begin{equation} \sigma = 393~\mrm{pm} \label{eq:6.6.6} \end{equation} \begin{equation} d = 127~\mrm{pm} \label{eq:6.6.7} \end{equation}

|
図 6.5. 得られた n-アルカン分子コアの比較。 図中の外側の実線は、5章の結晶のパッキングについての考察からえられた分子コアであり、 内側の実線はアルカンが球対称の構成単位からなっているとして部分分子容の加成則の係数から計算されたものである。 図の破線は、X線回析などからえられているアルカン分子骨格 [3.1b] の各炭素原子の上にそれぞれ半径 0.2 nm のファンデルワ-ルス球を描いたもの。 (メチル基のファンデルワ-ルス半径は 0.2 nm とされている[3.1a]) |
であった。 これらはいずれも、結晶のデ-タから予測されるものとよく合致している。 図 6.5 には5章で結晶のデ-タから得たアルカン分子のコアと、今回えたアルカン分子のコア、 さらにより実際に近い分子の形に似せたものとして各炭素原子上に直径 0.2 nm の球を設定したものを描いた。 異なる考察から得られたもの同士でありながらよく合致しているといえよう。
現実系との比較で次に問題になるのは、圧力・温度依存性である。 ファンデルワ-ルスの描像に忠実に考えるとこれはまず第一義的には溶媒の密度に対する依存性ということになる。 ここでは、もっとも直接的な密度依存性である圧力への依存性を調べる。
| 図 6.6. \(\alpha\) および \(\beta\) の圧力依存性の実測値(実線)と計算値(破線)。 実測値は純 n-アルカンについてのものであり、計算値は四塩化炭素溶媒中での n-アルカンの部分分子容についての計算。 純 n-アルカンのデ-タは[6.3]による。 |
実験的にある溶媒中での無限希釈の部分分子容の圧力依存性を系統的に検討したものは存在しない。 ここでは純アルカン液体についての配置の部分分子容についての加成則が無限希釈の部分分子容と同じ挙動をするものとして比較する。 加成則の係数を得るためのデ-タとしては5章で述べた Bridgman のものは精度が十分でないので、近年の Scaife-Lyon による測定結果[6.3]を用いた。 図 6.6 にみられるように \(\alpha\)、\(\beta\) ともに減少し、\(\beta\) の方が圧力依存性が大きいというおおまかな挙動に対しては計算と実験の一致がみられる。 定量的な一致という点では、\(\alpha\) についてはきわめてよく計算値は実験値を再現しているが、\(\beta\) については実験値は計算より大きな圧力依存性を示している。
このように、今回の圧力依存性に対する計算結果はおおまかには現実系の挙動をよく再現している。 このことは、液体・溶液に対するファンデルワ-ルスの描像の確かさを裏付けるものである。 このような成功の一方で、\(\beta\) について圧力依存性を過小に評価するという問題もあきらかとなった。 このことについてはまず、比較している実験値がある決まった溶媒中、無限希釈での部分分子容についての加成則から得られたものではなく、 純粋のアルカン液体から得られたものであることを考慮しなければならない。 この上でなおかつ \(\beta\) を過小に評価するとするなら、おそらく分子間ポテンシャルエネルギ-の斥力部分を単純な剛体的相互作用に置き換えたところを問題にしなければならないだろう。 今後の実験・理論の展開の中で、より問題の所在が明確になることを期待したい。