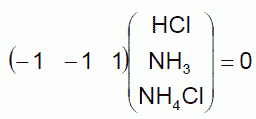３．反応方程式の複数の反応方程式への分解

１つの化学反応を複数の化学反応の結果として記述することで、 化学反応方程式の係数を決める作業を見通しよくすることができます。 またしばしばそうした作業は、反応の内実をよりよく理解し、新たな反応を設計する上で有効です。

少し抽象的なレベルで、次のアンモニアと塩化水素の反応を考えてみましょう。

HCl + NH₃ → NH₄Cl　　(3.1)

この反応を次の３つの反応に分けて考えることができます。

HCl → H⁺ + Cl^-　　(3.2a)
NH₃ + H⁺ → NH₄⁺　　(3.2b)
Cl^- + NH₄⁺ → NH₄Cl　　(3.2c)

ここでこの３つの反応の反応進行度 z₁、 z₂、 z₃ が、 いずれも塩化アンモニウムの生成反応の進行度 z に等しいとしています。 これは先のベクトル空間での議論で言えば、

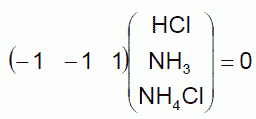　　(3.3)

で与えられる反応を、 新たに３つの化学種を加えて次元を拡張し、 次のような３つの化学反応に書き直したことに相当しています （３つ反応の反応進行度をz に等しくおいています）。

　　(3.4)

さらに言えば、両辺の元素の係数が釣り合うように係数を決めるという操作は、 元素から化学種を生成する反応に分解し、 それぞれの反応の反応進行度を決めているという風に見ることもできます （２章の(2.3a) (2.3b) 式では、反応進行度を等しく取り、量論係数を定める問題として設定していました）。 たとえば塩素酸カリウムが、塩化カリウムと過塩素酸カリウムに分解する反応、

4KClO₃ → KCl + 3 KClO₄　　(3.5)

を次の３つの反応に分解して考えるわけです。

K + Cl + 3O → KClO₃　　(3.6a)
K + Cl → KCl　　(3.6b)
K + Cl + 4O → KClO₄　　(3.6c)

この時、それぞれの反応の反応進行度 z₁、z₂、z₃ について、 次のような関係が成り立ちます。

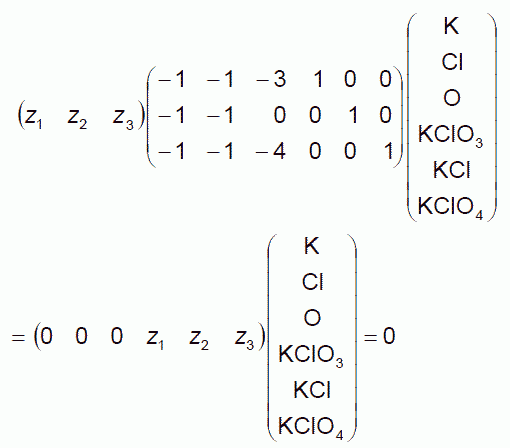　　(3.7)

これは次の関係式に帰着し、

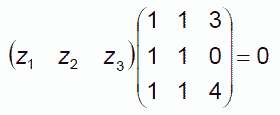　　(3.8)

ここから -z₁/4 = z₂ = z₃/3 = z。 (z₁, z₂, z₃) = (-4, 1, 3) z という結果を得、 これが化学量論係数を与えることになっています。

このように次元を拡張することで事態の見通しを得るのも、 化学者が日常的に行う操作の一つといえます。

次の章へ　前の章へ

表紙へ