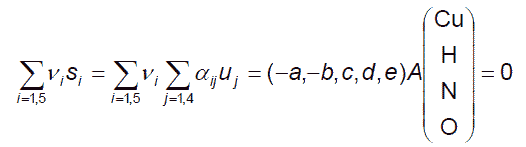 (2.7)
(2.7)
化学種は一般に数種の元素がある一定の比率で化合してできており、 元素 A の m mol と元素 B の n mol とから 1 mol の化学種ができる時、 その化学種を AmBn と表記します:*
mA + nB → AmBn (2.1)
物質不滅の法則 law of indestructibility of matter は、 こうしてできた化学種 AmBn を再び化学変化で元素に戻したとき、 同じだけの物質量の元素になるという法則だということができます:
AmBn → mA + nB (2.1')
物質不滅の法則から、化学反応方程式は反応によって化学種に含まれる元素の物質量が変化しないように構成されねばなりません。 たとえば
aCu + bHNO3 → cCu(NO3)2 + dH2O + eNO (2.2)
という反応であれば、次のような関係が成立します。
aCu + bHNO3 → aCu + bH + bN + 3bO (2.3a)
cCu + 2dH + (2c + e)N + (6c + d + e)O → cCu(NO3)2 + dH2O + eNO (2.3b)
(2.2) 式の反応進行度を x とした時、(2.3a)、(2.3b) 式に登場する Cu、H、N、Oそれぞれの(仮想的な)物質量について下記の式を得ます:
Cu: ax - cx = 0 (2.4a)
H: bx - 2dx = 0 (2.4b)
N: bx - 2cx - ex = 0 (2.4c)
O: 3bx - 6cx - dx - ex = 0 (2.4d)
ここから、(a, b, c, d, e) = (3, 8, 3, 4, 2)t、という結果を得ます(t は任意定数)。 通常、量論係数としては最小の整数比を採用するので、下式のように反応式が構成できます。
3Cu + 8HNO3 → 3Cu(NO3)2 + 4H2O + 2NO (2.5)
この操作をより一般的に表現するには、化学反応に関わる元素 N 個からなる N 次元の線形空間 W を考えるのが便利です。 ある化学種を表現する化学式(組成式)は、Wの中のベクトルを用いて表現できます ((2.1)、(2.1')式で表現される物質不滅の法則が、線型の関係を与えることに注意)。 たとえば (Cu, H, N, O)からなる4次元の空間の中で、硝酸は(0, 1, 1, 3)というベクトルに、 水は(0, 2, 0, 1)というベクトルに対応します。 こうした立場からは、量論係数を決める問題は、(1.4) 式で一般的に表した化学反応方程式を、 反応に関わる分子種を表現するベクトル Xi に関する下記の1次従属の関係を満たす係数を決める問題と見なすことになります。
∑ νi Xi = 0 (2.6)
もし反応に関わる分子種を表現するベクトルが1次独立であれば、そもそもそうした反応は起きません。 もう少し補うと、銅と硝酸の反応では次のような計算をしていたことになっています。
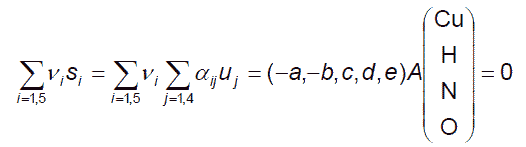 (2.7)
(2.7)
ここでAは下記の階数4の行列です(もし階数が 3 なら量論係数は一意には決まらない。後述)。
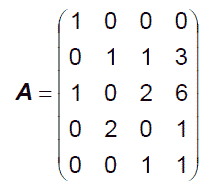 (2.8)
(2.8)
量論係数は次の連立1次方程式を解くことで決定できます。
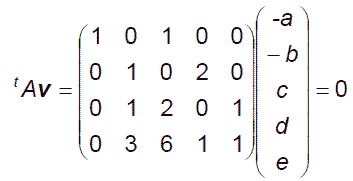 (2.9)
(2.9)
ここでは元素にまで還元して考えましたが、 多くの場合原子団レベルに還元することが事態の見通しをよくします。 たとえば次のようなステアリン酸ナトリウムと水酸化カルシウムから金属セッケンを作る複分解反応では、 (Na, C, H, O, Ca)についての釣り合いを考えなくとも、 (Na, C18H36O2, Ca, OH) = (A, X, B, Y) についての釣り合いを考えれば事足ります。
2NaC18H36O2 + Ca(OH)2
→ 2NaOH + Ca(C18H36O2)2 (2.10)
2AX + BY2 → 2AY + CX2 (2.10')
先の線形代数の言葉で言えば(Na, C, H, O, Ca)の5次元のベクトル空間の中で、 反応に関与する4つの化学種(Na, C18H36O2, Ca, OH) の張る4次元の部分空間を考えることに相当します (この反応を考える上で、1次独立な化学種の次元が元素の次元より1つ少ないことに注意)。 化学者は多くの経験を積む中で、(しばしば意識することなく)化学変化の中の独立な成分を抽出する能力を身に付けていくものの様です。
* 何でもないようですが、こうした化学種の定義には、一筋縄でいかない、化学量論とも深く関わる内実が隠されています。 この化学種の定義にまつわる問題については、補論を参照ください。