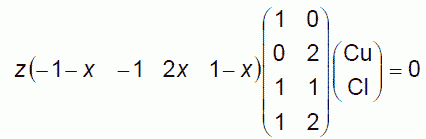６．化学反応方程式の自由度／基底の選択

次の反応に見るように、しばしば反応方程式の係数が（両辺の定数倍を除いて）一意的に決まらない場合があります。

a Cu + b Cl₂ → c CuCl + d CuCl₂　　(6.1)

この反応では、次のように量論係数に変化の余地があります（0 ≦ x ≦ 1）。

(1 + x) Cu + Cl₂ → 2x CuCl + (1 - x) CuCl₂　　(6.2)

あるいは次の2種類の反応で表現し、 それぞれの反応進行度が異なるものとして理解することもできます：

2 Cu + Cl₂ → 2 CuCl　　(6.3a)
Cu + Cl₂ → CuCl₂　　(6.3b)

この銅と塩素の反応を記述する際、 量論係数が整数にならないとする立場からは、 この反応が「非化学量論的」 non-stoichiometric であると呼び、 また生成物を CuCl と CuCl₂ の単なる混合物と見なさず、 生成物を「非化学量論的化合物」と呼びます。

先の行列を用いた表示では、元の式が次の形で書けると主張していることになっています。

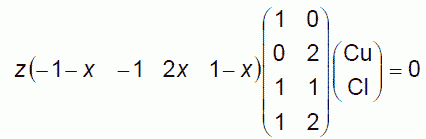　　(6.4)

この行列の階数が2であるため、(a, b, c, d)が一意的に決まらず、任意定数 x を含む形の解となります。 ２つの反応に分けて考えるのは、 行列から３つの行ベクトルを取り出して作った２つの量論係数のベクトルを用いて、 次のような形に解を求めたことに相当します（z₁ = x、z₂ = 1 - x）：

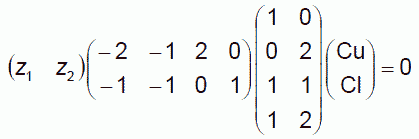　　(6.5)

取り出す行ベクトルの組としては他にも考えられ、量論係数ベクトルとして(-1, 0, 2, -1)といったものを考えてもかまいません。 この場合、たとえば次の２つの反応を独立に考えることになるわけです。

Cu + CuCl₂ → 2 CuCl　　(6.6a)
2 CuCl + Cl₂ → 2 CuCl₂　　(6.6b)

この塩化銅の生成反応は、直感的にも分かりやすいと思います。 けれども現実にはかなり込み入ったケースが登場してきます。 そうした例として、次のエタノールのヨードホルム反応についての化学反応方程式を見ておきましょう。

a C₂H₆O + b I₂ + c Na₂CO₃ + d H₂O → e CHI₃ + f NaI + g NaHCO₃　　(6.7)

この反応の量論係数の組 (a, b, c, d, e, f, g) で適切なものを決める問題を、当化学教室の３回生の皆さんにやってもらったところ、 次のような（いずれも化学量論的にはまちがいではない）答えが返ってきました：

(1, 5, 8, 2, 1, 7, 9)　　(6.8a)
(2, 9, 10, 1, 3, 9, 11)　　(6.8b)
(3, 14, 18, 3, 4, 16, 20)　　(6.8c)
(1, 4, 2, -1, 2, 2, 2)　　(6.8d)
・・・・・・・・
(6x-5, 2(11x-9), 2, -12x+11, 2(7x-6), 2x, 2(2-x))　　(6.8e)
(1, 6-x, -6x+14, 5-3x, x, -5x+12, -7x+16)　　(6.8f)
(3x, 13x+y, 12x+6y, 3y, 5x-y, 11x+5y, 13x+7y)　　(6.8g)

どの答えも、化学量論の要請を満たしていることは容易に確かめることができます。 ではどれが適切なのでしょうか？

この反応の量論関係について、次のように行列を使って表示することができます。

　　(6.9)

この行列の階数が５であるのに対し、量論係数のベクトルの次元は７ですから、 定数倍の因子を除いても、１つ自由度があることが分かります。 ですからさまざまな解がでてきても構わないのです。 その中のどれが“適切”なのかについては、もう少し進んだ“化学”の知識が必要になります。

おそらく「化学的」には先の関係式を、次のように２つの化学反応の組み合わせで表現するのが見通しがよいでしょう。

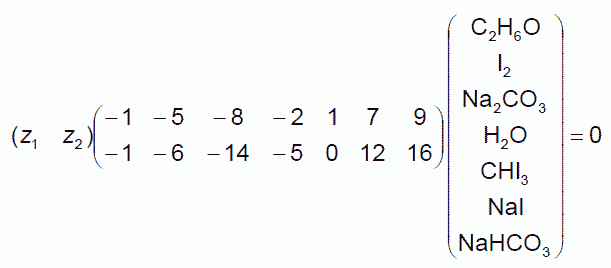　　(6.10)

通常の表記では、次の２つの化学反応方程式ということになります。

C₂H₆O + 5 I₂ + 8 Na₂CO₃ + 2 H₂O → CHI₃ + 7 NaI + 9 NaHCO₃　　(6.11a)
C₂H₆O + 6 I₂ + 14 Na₂CO₃ + 5 H₂O → 12 NaI + 16 NaHCO₃　　(6.11b)

一つはエタノールがヨウ素によって、ヨードホルムと炭酸に、もう一つは炭酸にまで酸化されてしまう反応です。 化学量論に閉じた世界の中では、 両者共に許されます。 あるいはこのベクトルを組み合わせて、エタノール 2 mol からヨードホルム 1 mol と炭酸 3 mol が生成する反応を考え、 それを独立なベクトルとしても構わないのです。

現実にはエタノール 1 mol からヨードホルム 1 mol が生成する、 あるいは有機化学の反応機構の知識があれば、 (6.8a) あるいは (6.11a) の反応方程式が適切であるということが分かります。 こうした観点から見ると、化学反応を解明するという作業の多くは、 化学量論で準備されたベクトル空間の中で“適切な”ベクトルの組み合わせを探ること、 といってよいかもしれません。

よく知られた反応ですが１章で取り上げた、過マンガン酸カリウムによる過酸化水素の酸化反応 (1.6) についても同様のことが言えます。 過マンガン酸カリウムによる過酸化水素の酸化反応も、化学量論に閉じた世界の中では、係数は一意に定まりません。 この反応を表現するのに、次の過マンガン酸カリウムと過酸化水素それぞれの分解反応を、独立な２つのベクトル（基底ベクトル）として取り上げてみましょう。

4 KMnO₄ + 6 H₂SO₄ → 4MnSO₄ + 2 K₂SO₄ + 5 O₂ + 6 H₂O　　(6.12a)
2 H₂O₂ → O₂ + 2 H₂O　　(6.12b)

この２つの反応を組み合わせることで、“適切”な反応方程式である (1.6) 式が組み立てられることは容易に見て取れるでしょう （(6.12a)×(1/2) + (6.12b)×(5/2)）。

2 KMnO₄ + 5 H₂O₂ + 3 H₂SO₄ → 2 MnSO₄ + K₂SO₄ + 8 H₂O + 5 O₂　　(1.6)

基底ベクトルに１次独立なベクトルの組の何を採用するかは任意ですから、 過マンガン酸カリウム、過酸化水素それぞれの分解反応(6.12a)、(6.12b) から、 “適切”な反応方程式 (1.6) 式を構成できることは当然です。 けれどもヨードホルム反応の場合と同様に、(6.12a)と (6.12b) から構成される、 化学量論的には正しい反応方程式の中から、どのようにして“適切”な反応方程式を見出すかはまた別問題です。

2 KMnO₄ + 3 H₂O₂ + 3 H₂SO₄ → 2MnSO₄ + K₂SO₄ + 6 H₂O + 4 O₂　　(1.6')
2 KMnO₄ + 7 H₂O₂ + 3 H₂SO₄ → 2 MnSO₄ + K₂SO₄ + 10 H₂O + 6 O₂　　(1.6'')
・・・・・・

一見単純に見える(6.12a)、(6.12b)を基底ベクトルに選択したからといって、 過マンガン酸カリウムと過酸化水素の間の反応の“適切”な反応方程式がただちに構成できるわけではありません。 “適切”な反応方程式を構成するには、 過マンガン酸カリウムと過酸化水素の反応に直接関わる分子種に注目し、 そこに“化学的”な知見を動員するという手法が有効です。 ５章で取り上げた半電池反応を用いる手法の有効性は、こうした問題を扱うときにはっきりします。 半電池反応の手法では電子の授受に注目して基底ベクトルを構成し、 ここで考慮すべき反応は次の３つに整理できます。

MnO₄^- + 8 H⁺ + 5 e^- → Mn⁺² + 4 H₂O　　(6.13a)
H₂O₂ → O₂ + 2 H⁺ + 2 e^-　　(6.13b)
H₂O₂ + 2 H⁺ + 2 e^- → 2 H₂O　　(6.13c)

(6.12)では独立な反応（基底ベクトル）は２つでしたが、分子種（電子）を１つ増したために、 基底ベクトルが１つ増えて３つになりました。 この拡大されたベクトル空間で、（化学の知識から）過酸化水素が還元される（酸化する）反応である (6.13c) が起きないものとします。 そして(6.13a) (6.13b)を組み合わせることで、 次の反応方程式を得ます。

2 MnO₄^- + 5 H₂O₂ + 6 H⁺ → 2 Mn⁺² + 5 O₂ + 8 H₂O　　(6.14)

イオン式でなく中性の分子種で書き直せば、先の反応方程式(1.6)を得ます。

2 KMnO₄ + 5 H₂O₂ + 3 H₂SO₄ → 2 MnSO₄ + K₂SO₄ + 8 H₂O + 5 O₂　　(1.6)

つまり一端分子種を増やして考えるべき反応方程式の次元を拡大した後、 そこから実際の反応には関与しないと（化学的な知識・経験から）判断される基底ベクトル（過酸化水素が還元されて水になる反応）を切り離し、 全体の反応方程式を再構成したわけです。

同様のことを、最初に考えた独立な基底 (6.12a) と (6.12b) からなるベクトル空間で行なうことも可能ではあります。 しかし(6.12a) と (6.12b) というベクトルは、(6.13a)～(6.13c)を基底とする空間の中では複雑な構成を持ちます。 過酸化水素の分解反応 (6.12b)はまだしも簡単で (6.13b) + (6.13c) ですが、 過マンガン酸カリウムの分解反応(6.12a)は、(6.13a)×4 + ((6.13c)×(-1) + (6.13b))×5 という線形結合になります （(6.13c)×(-1) + (6.13b) は水の分解反応 2 H₂O → O₂ + 4 H⁺ + 4 e^- に対応）。 この (6.12a) と (6.12b) から、過酸化水素が還元されて水になる反応 (6.13c)を切り離すのは厄介です。

ちょっとくだくだしい話になりましたが、 化学量論で取り扱うベクトル空間の中で“適切な”ベクトルを探り出す営みの一つの形を感じていただけたでしょうか？

最後に、次の4つの化学反応が同時に起きたとして、それぞれの反応の反応進行度が、 Cu, Cl₂, CuCl₂, CuClの物質量からは一意的に定まらないことを注意しておきます。

2 Cu + Cl₂ → 2 CuCl
Cu + Cl₂ → CuCl₂
Cu + CuCl₂ → 2 CuCl
2 CuCl + Cl₂ → 2 CuCl₂

このような場合、こうした４種の化学反応を考えることにそもそも意味がないという立場もありえます。 その一方、反応進行度の時間依存性（→反応速度）と反応物の物質量の間に何らかの簡単な関係を想定する立場からは、 反応物の物質量の時間変化を予測する上で有用であるとの立場もありえます。

次の章へ　前の章へ

表紙へ