
|


|
| 図1a. 簡易赤外吸収測定セルの構成パーツ。 外径 10 mm 長さ 2 ~ 3 cm のアクリルのパイプの両端に、 シリコンの窓をテフロンのキャップで嵌める。 | 図1b. 取りあえず組み立てたところ。 アクリルのパイプに開けた 2 mm ぐらいの穴から、 キャピラリー管やパスツールピペット、マイクロピペットなどで、 濃塩酸をセル内に入れます。 |
赤外活性である代表的な二原子分子としてHClを取り上げ、 その赤外吸収スペクトルに現れる振動回転線を解析することにより、 核間距離と回転温度を算出する。 また、重水素置換したDClを用いて赤外吸収スペクトルにおける同位体効果に触れる。
塩化水素の赤外スペクトルの測定とその解析は、 振動分光の実験の定番と言ってもいいでしょう。 塩化水素の回転定数は 10 cm-1 程度と大きく、 少々装置の分解能が低くても、教科書にある分光学のおはなしが、 実際に成り立つことをかなりの精度で確認できます。 というわけで、細かい計算を要する課題の数もちょっと多めです。
塩化水素は腐食性があり、 呼気やメタンを測るようなわけには行きません。 また水があると容易に吸収されてしまいます。 ここではそこを逆手に取って、 濃塩酸(35 %)から出てくる塩化水素を、 図 1 に示すような簡易な光学セルを使って測ってもらいます。 新鮮な濃塩酸であれば蒸気を吸って注入すれば測定できるのですが、 重塩酸(お高いので量が少ない)が湿気を吸って濃度が下がっていたり、 セル内の湿気等に吸収されるのか、みるみる濃度が低下することがあったりで、 液滴を加えるのが確実なようです。
以前は塩化ベンゾイル PhCOCl と水(あるいは重水)の反応で塩化水素の気体を発生させ、 専用の気体セルを用いて、真空系を用いて測定したりもしていました。 この塩化ベンゾイルと水の反応が結構厄介で (水を入れすぎると塩化水素が水に溶けて出てこない。 生成する無水安息香酸が固結する etc)、 また発生した塩化水素を液体窒素でトラップして使用することにしていたのですが、 下手に扱うと破裂の危険もあり、大変気を遣う実験でした。 とても30人ぐらいの学生を1週で面倒みられるものではありません。
窓材にはシリコンを採用しています(「渡邊 window」)。 見た目、金属のようで光を通さないように見えますが、 およそ 1500 ~ 9000 cm-1 の赤外~近赤外領域についてはほとんど吸収がなく、 また塩酸に侵されたりしません (ただし屈折率が大きく、表面の反射率が大きいのが難)。

|


|
| 図1a. 簡易赤外吸収測定セルの構成パーツ。 外径 10 mm 長さ 2 ~ 3 cm のアクリルのパイプの両端に、 シリコンの窓をテフロンのキャップで嵌める。 | 図1b. 取りあえず組み立てたところ。 アクリルのパイプに開けた 2 mm ぐらいの穴から、 キャピラリー管やパスツールピペット、マイクロピペットなどで、 濃塩酸をセル内に入れます。 |
cary 630 の透過型ユニットは、 赤外光がおよそ 2 mm ぐらいの光束で透過するように設計されているようです。 図 2 のように液晶サーモグラフシートを差し込んでみると、 赤外光が当たった部分の色が変わるので、 光路の位置と光束を確認できます。

|

|

|
| 図2a. 液晶サーモグラフシート。 指で触ったところの色が変わっている。 | 図2b. cary 630 の透過型ユニットの赤外光が通っていると思しき所に差し込む。 | 図2c. 赤外光が当たったところの色が変わっている。 |
先の簡易赤外吸収測定セルは、 透過測定用の標準の金属製ホルダーに嵌めた、 テフロン製(自作)のホルダーに固定します。 空の状態でバックグラウンドを取った後、 一端取り出して、塩酸を注入すのがお薦めです。 透過ユニットの中で注入操作をすると、 塩酸を漏らしたりして、 透過ユニット内に塩化水素の蒸気が入り、 ミラーが曇ったりする心配があります。 また、できれば測定中は、 局所排気装置で周辺を排気するようにします。

|

|

|
| 図3a. 簡易赤外吸収測定セルとホルダー。 ホルダーの穴にアクリルパイプを通し、 窓を取り付ける。 テフロンキャップが外れないように、 シールテープを巻いておくとよい。 | 図3b. ホルダーに取り付けた簡易赤外吸収測定セル。 | 図3c. 透過測定ユニットに収まった簡易赤外吸収測定セル。 まずは空の状態でバックグラウンドを測定した後、 取り出して塩酸を注入。 再びセットして赤外吸収を測る。 |
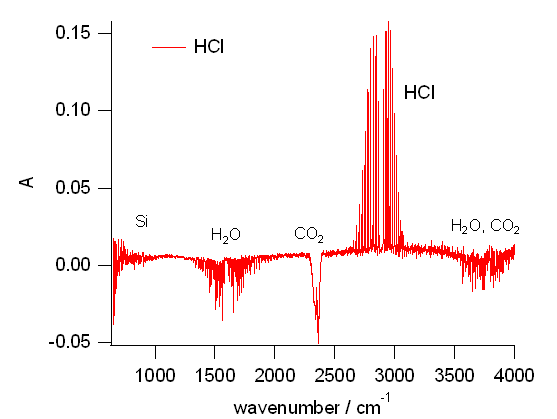
取りあえず今回の測定でどのようなスペクトルが得られるか、 図 4 に塩化水素 HCl についての結果を示します。
シリコンの窓を使っているので、 1500 cm-1 ぐらいより低波数側には、 バックグラウンド測定で除ききれないシリコンによる吸収の影響が現れてきます。 特に 1000 cm-1 より低波数側ではシリコンの吸収が大きくなります。 またバックグラウンド測定で二酸化炭素や水の吸収の影響を除くわけですが、 バックグラウンド測定での吸収が大きいと、 見かけ上発光している(吸光度が負)ように見えます。 幸い、塩化水素 HCl の吸収は、二酸化炭素や水の吸収の影響がほとんどない 2600 ~ 3100 cm-1 の領域に現れるので、 後の解析に支障ないスペクトルをえることができます。
このスペクトルの回転線について詳細な解析を行ってもらうわけですが、 ざっくり観察してみると、 二酸化炭素の逆対称伸縮運動の吸収のように、 中央の Q 枝がなく、 左右に回転運動による吸収帯 P 枝と R 枝の櫛状のピークが広がる構造をしています。 櫛状のピークの間隔はだいたい 20 cm-1 で、 P 枝と R 枝の間には一本欠けています。 また間隔は高波数側に行くにしたがって少し狭まり、 R 枝全体の幅が P 枝に比べて少し狭まっていて、 二酸化炭素の逆対称伸縮運動の吸収と似通っています。
|

|
| 図 4a. 塩化水素 HCl について得られた赤外スペクトル。 1500 cm-1 ぐらいより低波数側には、 窓に使用しているシリコンの影響が現れる。 またバックグラウンド測定で水や二酸化炭素の影響を差し引きすぎて、 「発光現象」が現れたりする。 | 図 4b. 得られた塩化水素 HCl の赤外吸収スペクトルの拡大図。 Q 枝は現れない。 ほぼ等間隔の櫛型のピークが現れるが、高波数側に行くにしたがって、間隔が若干狭まっているように見える。 |
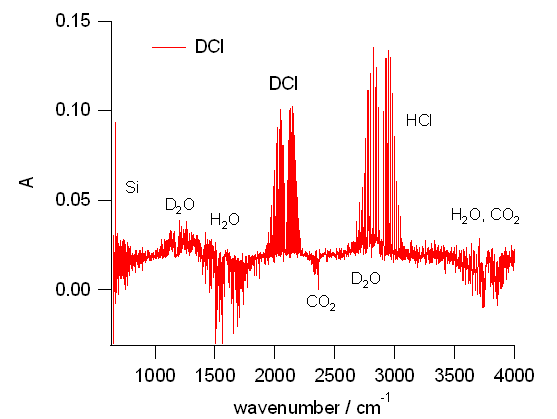
図 5 には塩化重水素 DCl についての結果を示します。 もとの試薬は重水素 D 置換 99.5 % といったものなのですが、 ドライボックスなど使用していないので、 空気中の湿気を吸って、 HCl の吸収が出てきます (HCl の吸収の大きさは、どれぐらい手早くセットできるかにもかかっています)。 また重水 D2O、軽重水 HDO の吸収も出てきます。 幸い、塩化重水素 DCl の吸収は、DCl の実効質量(\(m(\mrm{D})m(\mrm{Cl})/(m(\mrm{DCl})\))が HCl の ほぼ2倍で、 およそ HCl の吸収帯の \(1/\sqrt{2}\) の 2100 cm-1 付近で、 HCl の吸収から 900 cm-1 近く低波数側に現れて、 HCl は無論、他の分子の吸収の影響もほとんど受けません (少し P 枝に H2O の吸収帯の影響がかかる)。
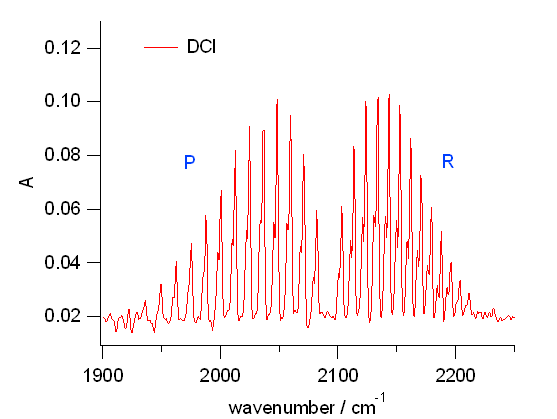
図 5b には DCl の吸収を拡大して示しています。 図 4b の HCl の挙動と似通っていますが、 一見、大きく違うのは櫛状のピークが高波数側に行くにしたがって、 2本に分裂していくことでしょう。 これは検討課題の3番にもあるように、 Cl に 35Cl と 37Cl の同位体が存在することに由来しています。 またもう少し細かく見ると、 櫛状のピークの間隔はだいたい 10 cm-1 で、 HCl の約半分。 吸収帯の幅はおよそ 300 cm-1 で HCl の 半分とはいかず、 7割ぐらいに狭まっています。
|
|
| 図 5a. 塩化重水素 DCl について得られた赤外スペクトル。 空気中の湿度を吸って HCl の吸収も出てくる。 D2O 由来の 2700 cm-1 付近の吸収は、 HCl の P 枝と重なっている。 HDO の変角振動は判然としない。 | 図 5b. 得られた塩化重水素 DCl の赤外吸収スペクトルの拡大図。 HCl の吸収のほぼ \(1/\sqrt{2}\) の位置によく似た形状で現れるが、 35Cl と 37Cl の同位体による櫛型のピークの分裂が顕著で、 櫛型のピークの間隔はほぼ 1/2。 |
塩化軽水素 HCl に比べて、塩化重水素 DCl で 35Cl と 37Cl の振動数の差が明瞭になるのは、 振動数が実効質量 \(\mu\) の平方根に反比例することから、 次のように示すことができます。
X-Y という二原子分子を考え、 一方の Y の質量 \(m_\mrm{Y}\) を微小量変化させた時の振動数の変化は次のように表されます:
\begin{equation} \frac{1}{\nu (\mrm{XY})} \frac{\rmd \nu (\mrm{XY})}{\rmd m(\mrm{Y})} = \frac{\rmd \ln \nu (\mrm{XY})}{\rmd m(\mrm{Y})} = -\frac{1}{2} \frac{\rmd \ln \mu (\mrm{XY})}{\rmd m(\mrm{Y})} = -\frac{1}{2} \left(\frac{1}{m(\mrm{Y})} - \frac{1}{m(\mrm{XY})} \right ) = -\frac{1}{2} \frac{m(\mrm{X})}{m(\mrm{Y}) m(\mrm{XY})} \label{eq:difY} \end{equation}
ここで X を H、Y を Cl として、 35Cl を 37Cl にしたとすると、 HCl の場合の波数の変化は次のように評価できます。
\begin{equation} \Delta \tilde{\nu}(\mrm{HCl}) = \tilde{\nu}(\mrm{H{}^{37}Cl}) - \tilde{\nu}(\mrm{H{}^{35}Cl}) \approx -\frac{1}{2} \frac{m(\mrm{H})}{m(\mrm{\mrm{{}^{35}Cl}}) m(\mrm{\mrm{H{}^{35}Cl}})} \Delta m(\mrm{Cl}) \tilde{\nu}(\mrm{H{}^{35}Cl}) \\ \approx -\frac{1}{2} \frac{1}{35 \times 36}~\times 2 \times 2900~ \mrm{cm^{-1}} = -2.3~ \mrm{cm^{-1}} \end{equation}
ここで \(\Delta m(\mrm{Cl}) = m(\mrm{{}^{37}Cl}) - m(\mrm{{}^{35}Cl})\) です。 装置の分解能が 2 cm-1 ですから、 ぎりぎり見えるかどうかというところで、 実際、HCl の回転線を拡大すると少し低波数側に膨らんでいることが確認できます。 では DCl の場合にはどうかを考えると、 振動数\(\nu(\mrm{DCl})\)は実効質量が HCl のほぼ 2 倍なので HCl の \(1/\sqrt{2}\) になり
\begin{equation} \Delta \tilde{\nu}(\mrm{DCl}) \approx -\frac{1}{2} \frac{m(\mrm{D})}{m(\mrm{\mrm{{}^{35}Cl}}) m(\mrm{\mrm{D{}^{35}Cl}})} \Delta m(\mrm{Cl}) \tilde{\nu}(\mrm{D{}^{35}Cl}) \\ \approx -\frac{1}{2} \frac{2}{35 \times 37}~\times 2 \times \frac{1}{\sqrt{2}} \tilde{\nu}(\mrm{H{}^{35}Cl}) \approx \sqrt{2} \Delta \tilde{\nu}(\mrm{HCl}) = -3.3~ \mrm{cm^{-1}} \end{equation}
X-Y という分子で(\(m(\mrm{X}) \ll m(\mrm{Y}) \))、Y の質量 \(m(\mrm{Y})\) を変化させた時、 振動数の変化率は X の質量 \(m(\mrm{X})\) にほぼ比例するとみなせ(式\eqref{eq:difY})、 一方振動数は \(m(\mrm{X})\) の平方根にほぼ反比例(\(\mu \approx m(\mrm{X})\))しています。 その結果、D35Cl と D37Cl の振動数の差はHCl の場合の\(\sqrt{2}\) 倍になって、 装置の分解能が 2 cm-1 でも十分見えるというわけです。
なお回転定数は慣性モーメントに反比例するので、 35Cl の回転線の方が37Cl の回転線より、 間隔が広くなります。 ですから高い回転順位の関与する R 枝の回転線は、 35Cl のピークは37Cl のピークより、 より高波数側に出ることになり、 P 枝の回転線ではより低波数側に出ることになります。 このため R 枝側では、元の基準振動における35Cl と 37Cl の差がより拡大され、 逆に P 枝側では差が縮小するため、 P 枝側のピークの分裂が見えにくくなっています。
検討課題にあるように、 測定した HCl と DCl について回転線のピークを読みとってもらうのですが、 「どこを」「どこまで」読むのかは論点です。
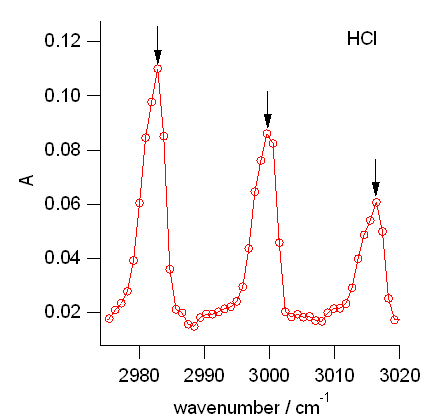
まず「どこを」読むかですか、 DCl でははっきりしていますが、HCl でも 35Cl と 37Cl の同位体に起因する、 ピークの分裂、ピークの非対称性が現れます。 今回の場合、スペクトルデータが 0.93 cm-1 おきに与えられていますが、 取りあえず一番大きな吸光度を与える波数を読んでもらえばいいでしょう。 つまり H35Cl、D35Cl に注目して、 その回転線を読む立場をとり、 ピークの重なりによる形状の変化には目をつぶるわけです。
|
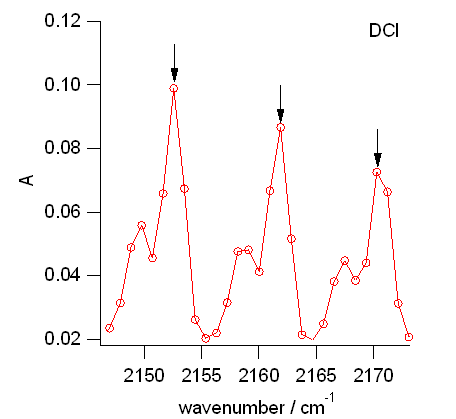
|
| 図 6a. HCl の回転線でも R 枝側では、H37Cl の影響で、ピークが少し低波数側にふくらむ。 ともかく一番高いところの波数を読む。 | 図 6b. DCl の回転線では、H37Cl の影響でピークが少し割れるのも見える。 割れた方のピークは無視して、一番高いところの波数を読む。 |
次に問題は「どこまで」読むかです。 装置の分解能が 2 cm-1 ですから、 1 cm-1 まで取れば十分なように思えます (データ点も 0.93 cm-1 間隔)。 でもわずかでも得られた情報を完全にすくい取るため、 0.1 cm-1 まで読んでおいてください。 というのは、利用できるピークの数を \(N\) 本程度とすると、 不確かさがほぼ \(1/\sqrt{N}\) のオーダーに縮小されることが期待できるからです (ここら辺の理屈は資料編の最小2乗法の項を参照。0.01 cm-1 まで記録するのはムダ)。
回転線の解析は、検討課題に沿い、解説の処方箋にしたがって、 用意してある excel のシートを使って進めていってもらえばよいでしょう (シートには HCl についての詳細な解析が紹介してありますが、 DCl についてもこれに則って解析してください)。 採用しているのは結合差法(method of combination differences)という手法に沿ったものですが、 一歩一歩、 櫛型のピークの構造に分け入っていく雰囲気が、 何か”ジャングル探検隊”のようで興味を持ってもらえるのではないかと思います。 ただ、ドライに事を進める立場からは、 次のようなことをやってみるのもありでしょう。
解説にあるようにHCl の回転線は、 遠心力ひずみの影響を無視すれば、 R 枝、P 枝 それぞれについて、角運動量の量子数 \(J\)、 基底状態(\(v = 0\))の回転定数 \(B\)、励起状態(\(v = 1\))の回転定数 \(B'\) を用いて、 \(J\) の2次関数になります。 そこに遠心力ひずみの影響が加わるとして、 それは \(J\) の2次以上の項に影響してくるはずです。 そこで取り合えず3次以上の項を無視して、次の形になるものとします。
\begin{equation} \tilde{\nu}_\mrm{R}(J) = \tilde{\nu}_0 + 2B' + (3B' - B) J + C_\mrm{R} J^2 \label{eq:Rbranch} \end{equation}
\begin{equation} \tilde{\nu}_\mrm{P}(J) = \tilde{\nu}_0 - (B' + B) J + C_\mrm{P} J^2 \label{eq:Pbranch} \end{equation}
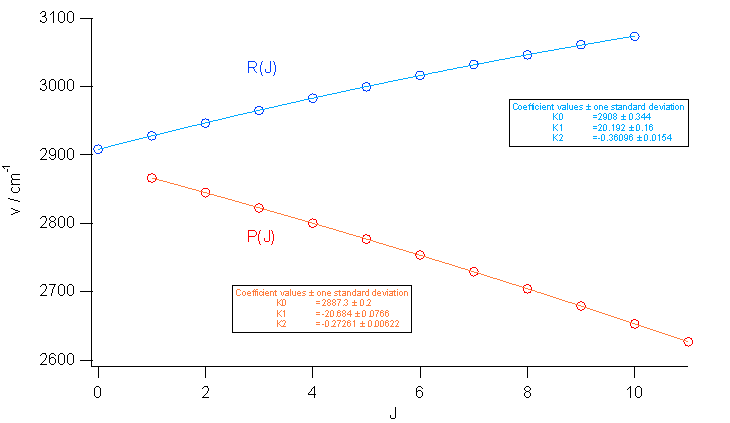
もし遠心力ひずみの影響がなければ、\(C_\mrm{R} = C_\mrm{P} = B' - B ~(\lt 0) \) です。 取り合えず \(J \)についての2次式に R 枝、P 枝のピーク位置を最小2乗法で当てはめてみた結果を図 7 に示します (このあたりは Igor のお得意なところ)。
|
|
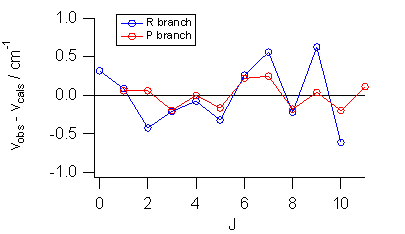
| 図 7a. 用意してある excel のシートの塩化水素 HCl の R 枝、P 枝の吸収線の \(J\) 依存性を \(J\) の2次式に最小2乗法で当てはめた結果。 | 図 7b. 当てはめた2次式からの実験値の偏倚。 |
高次の項を入れずとも、2次式でR 枝、P 枝のピーク位置の当てはめはできています。 ただし\(C_\mrm{R} \ne C_\mrm{P}\) で、遠心力ひずみの影響は無視できないようです。 また当てはめ結果の1次の係数から得られる励起状態(\(v = 1\))の回転定数は \(B' = 10.22~ \mrm{cm^{-1}}\) となり、 0次の係数(2908.0 cm-1 と 2887.3 cm-1)の差から得られる \(B' = 10.4~ \mrm{cm^{-1}}\) と一致していて (一般に当てはめの端点でのパラメーターの評価の誤差は大きい)、 式 \eqref{eq:Rbranch} と 式 \eqref{eq:Pbranch} のように、 3次以上の項を無視した近似が悪くないものだったことを裏付けています。
得られた回転定数から、 慣性モーメントを求め、結合距離を評価してもらうのですが、 この最後のところでも慎重さを失わないでください。 回転定数の精度は 1/1000 オーダーあります。 慣性モーメントから結合距離を求めるには、 実効(換算)質量が必要ですが、 それには平均原子量を使ってはいけません。
ピーク位置を読むところで注意したように、 あくまで H35Cl あるいは D35Cl を見ているのですから、 DCl の実効質量の計算には D の原子量 2.0141、35Cl の原子量 34.969 を使いましょう(資料編 III-10 参照)。 さらに言うなら、ボルン-オッペンハイマー近似を使っていることを思い出してもらうと、 原子核の質量を使う必要があり、 原子量から電子の質量を差し引くことになります (今回の実験の精度では関係ないですが)。
R 枝、P 枝の吸光度のそれぞれのピークの強度 \(A(J)\) が、 振動基底状態 \(v = 0\) における回転順位の存在量に比例するなら、 解説にある回転振動分布の式を、 エネルギー換算表を使って書き換えると、 \(A(J)\) は次のような関数に当てはめられることが期待されます。
\begin{equation} A(J) = A_0 + C (2J + 1) \exp \left[ -\frac{1.4388 (B / \mrm{cm^{-1}}) J(J + 1)}{T / \mrm{K}} \right] \label{eq:Jdistrx} \end{equation}
ここで \(A_0\) はセルのぐらつき等による、 吸光度のベースラインの変動量です。 ですから測定された吸光度のピーク強度データ \(A(J)\) を
\begin{equation} f(J) = a_0 + a_1 (2J + 1) \exp [ -a_2 J(J + 1)] \label{eq:Jdistr_fitfunc} \end{equation}
という関数に最小2乗法であてはめ、 得られたパラメータ \(a_2\) から
\begin{equation} T / \mrm{K} = \frac{1.4388 B / \mrm{cm^{-1}}} {a_2} \label{eq:Jdistr_T} \end{equation}
の関係から温度が求められるということになります。
温度を求めるシナリオとしてはこれでよいのですが、 実際にやってみると、 出てくる温度が数10~ 100 K ぐらいはずれることはめずらしくありません。
これにはいくつか原因が考えられるのですが、 測定上の問題として、 無論ノイズの影響はありますが、 回転線が鋭いために、 装置の分解能の影響を強く受け、 注目する中心波数から外れたところの吸収が低めに見積もられたりする問題があります (原子吸光分析では、分析光にそれぞれの原子の鋭い発光線を利用します)。 また吸光度が正しく測られたとして、 用意してあるレポートシートの設問にもありますが、 \((v = 0, J) \rightarrow (v = 1, J \pm 1) \) の吸光係数が \(J\) によらないという前提に問題があります。
振動スペクトルの構造から温度に迫るというアプローチは、 不安定分子種の非平衡状態での温度や遠い星の温度を評価したりする上で有効なのですが、 正確な温度の評価にはいろいろ考慮すべき点があることを知ってもらえればよいでしょう。
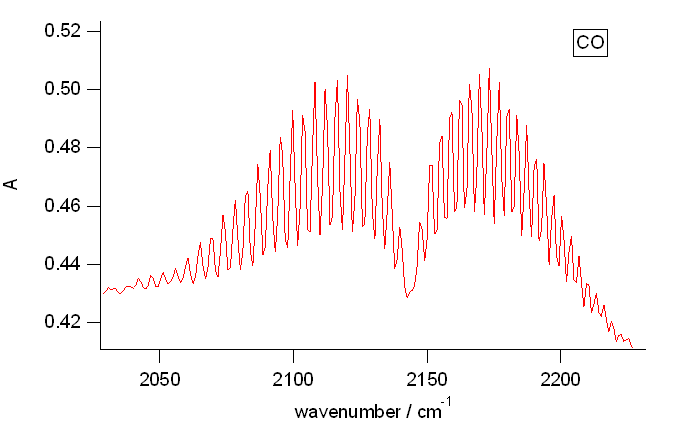
振動回転スペクトルの実験には、 今回使用した塩化水素以外に、 一酸化炭素 CO も用いられることがあります。 図 8 にCary 630 で測ってみた CO の振動回転線と、 結合差法によるプロットを示します (CO はギ酸と濃硫酸で発生)。 CO では \(B\) と \(B'\) がほぼ同じで、 遠心力ひずみの効果が小さく。 あまり余計なことを考える必要がありません。 けれどもそれだけ課題として奥行きがないとも言え、 塩化水素と「教育的」にどちらがよいか、 難しいところですね。
なお一酸化炭素のスペクトルは、 以前使用していた FTIR 装置のバックグラウンド測定で現れ、 当時担当していただいていた堀尾さんといろいろ相談して CO と判明。 どうも装置内のプリント基板あたりから発生していることが分かった (少し焦げ臭かったです)、 個人的には少し思い入れのあるスペクトルです。
|
|
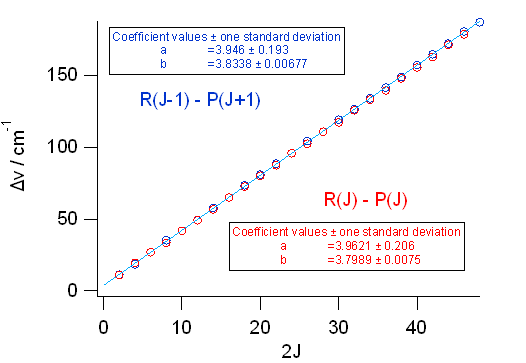
| 図 8a. 一酸化炭素 CO の振動回転線 | 図 8b. CO の結合差法による解析。 |