last revised 2020.11 / 2020.10
吉村洋介
0.物理化学・物性化学実験の準備
I. 電解質溶液の電気伝導度の測定と電気伝導度滴定
<概要>
電解質溶液の電気伝導度G(S cm-1単位で表されることが多い)は、
概ね、溶存しているイオン種の濃度と比例関係にあるとみなすことができる
(精度の高い測定では電気伝導度の濃度依存性が問題となるが、ここでは無視する)。
\begin{equation}
G = \sum_i \nu_{i} \mathit{\Lambda}_{i} c_{i}
\label{eq:econ}
\end{equation}
ここで\(\nu_i\) はイオン種 \(i\) の電荷の大きさ、\(c_i\) は濃度で、
\(\mathit{\Lambda}_{i}\)は当量電気伝導度と呼ばれるイオンの単位電荷当たりの電気伝導度を表す量。
室温水中でのアルカリ金属イオンなどの当量電気伝導度はおよそ数十 S cm2 mol-1 の値を持つ
(海水の電気伝導度は約 40 mS cm-1。
ニクロム線などの抵抗線の電気伝導度は 1 MS m-1 程度で桁違いに大きく、
銅などはさらにこの100倍程度大きい)。
水素イオン、水酸化物イオンの電気伝導度は例外的に大きく、水素イオンは350 S cm2 mol-1 、
水酸化物イオンは 200 S cm2 mol-1 程度の値を示す。
電解質溶液の電気伝導度の測定は、電極表面における電気化学的な過程が関わる結果、
さまざまな因子に配慮して行なう必要がある。
たとえば通常のマルチメーター(デジタルテスター)は、直流を流した場合の電流と電圧の関係から、
オームの法則に従って電気抵抗を評価・表示するので、そのままでは電解質溶液の電気伝導度を測るのには適切でない。
ここではマルチメーターを用いた単純な電気測定を通してその一端に触れる。
<試薬>
- 0.010 mol/L塩化ナトリウム溶液(用意してある 0.10 mol/L 溶液を希釈して調製)
- 0.10 mol/L塩酸(用意してある 1.0 mol/L 塩酸を希釈して調製)
- 0.10 mol/L水酸化ナトリウム溶液(用意してある 1.0 mol/L 溶液を希釈して調製)
IA. 電極の作成と電解質溶液の電気伝導度
- 用意されているステンレスの針金を 15 cm 程度の長さに切ったものを2本用意し、
それぞれを、5 cm程度直線状の部分を残して渦巻き状に巻いて電極を作成する。
- ビーカーに電極をビニルテープ等で固定するか、割りばしの先に電極をビニルテープでくくりつけるかして、
電気伝導度測定装置を作る。【先輩たちが作成したものがあれば流用してもよい】
- ビーカーに 0.010 mol/L 塩化ナトリウム溶液を入れて電極を浸し、
マルチメーターU1251Aの抵抗測定モードで電極間の抵抗値を測定する。
しばらく放置し、抵抗値の変動が小さくなったら、マルチメーターを電圧測定モードに切り替え、
電位が発生していることを確認する。
- マルチメーターのプローブをつなぎ替えて極性を変え、
再び抵抗測定モードで電極間の抵抗値を測定する。
しばらくして抵抗値の変動が小さくなったら、マルチメーターを電流測定モードに切り替えて測定する。
<検討課題>
- マルチメーターの抵抗測定モードを用いた電気抵抗測定の知見(上記(3)と(4))はどのように説明できるか考察せよ
(マルチメーターU1251Aの抵抗測定モードでは、抵抗のレンジが500 Ω で1.02 mA、5 kΩ で416 µA、
50 kΩ では41.2 µAの直流電流を通じて電圧を測定し、
オームの法則から抵抗を測る仕様となっている)。
IB. 交流を用いた電解質溶液の電気伝導度の測定
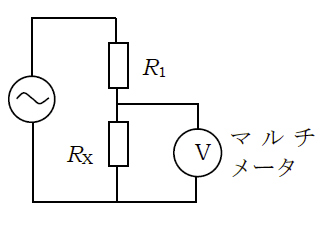
- 抵抗 R1(20~100 kΩ 程度)を介して、
IAで作成した溶液に浸した電極を電子天秤 AS402F 附属の電源アダプター(AC 100 V/AC 約15 V)に接続し、
右図のような回路を構成する(RX が溶液に浸した電極に相当)。
- 抵抗 R1 にかかる電圧V1、
電極間にかかる電圧 VX を測り電極間のコンダクタンス 1/RXを
VX/RX = V1/R1
の関係から求める(マルチメーターの入力抵抗は十分大きい)。
- 100 mLのビーカーにイオン交換水60 mL(適宜増減してよい)と0.10 mol/L塩酸5 mLを入れ、
電極を浸して回路に電流を流し、抵抗R1にかかる電圧V1、
電極間にかかる電圧 VXを測り、電極間のコンダクタンス 1/RXを(2)と同様にして求める。
- 0.10 mol/L水酸化ナトリウム溶液を1.0 mL(ポリエチのスポイトで取る程度で可)ずつ10 mL程度滴下して、
コンダクタンスの変化を測定する。
<検討課題>
- 電極の面積 S、電極間の距離 L を見積もり、塩化ナトリウムのモル電気伝導度 Λ を評価せよ
(濃度を c として 1/R = ΛcS / L の関係が成り立つとする)。
- 横軸に加えた水酸化ナトリウム溶液の量、縦軸にコンダクタンスを取って、
中和反応にともなう電気伝導度の変化をプロットせよ。
実験例
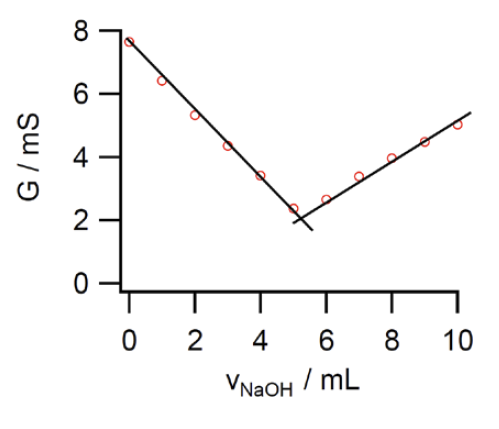
|
図I-1. 水酸化ナトリウム溶液滴下にともなう塩酸の電気伝導度変化例。
|
電解質溶液の電気伝導度の測定のこと
「塩水が電気を通す」のは誰もが知っています。
けれどもそのことと”電気抵抗”の関係となると、
理学部の3回生でも引っかかります。
以前はこの準備実験の前に、こんなクイズをやってもらっていました:
テキストにあるようなステンレス製の電極を2本、食塩水に浸す。
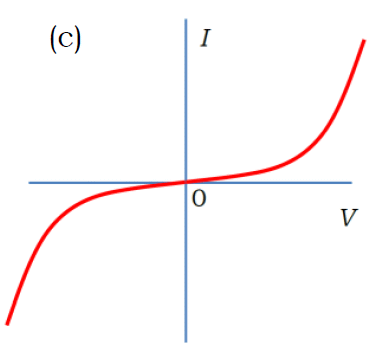
電極間に直流を流し、ゆっくり ±数Vの範囲で電圧 V を変化させたときの電流 I の変化を表す図として、適切なものを選べ。
この実験は2回生向けの実験(入門化学実験)でやっていて、
2回生向けの実験をとっている人は、たいてい、正解の (c) を選んでくれます。
でもこのクイズ、実際にやったことがないと結構迷います。
この実験では電気分解が起きるはずです。
水の電気分解には1.2 V くらいは必要で、それぐらいはかけないと電流は流れないでしょう。
でも塩水は電気を通すはずで、電圧をかけさえすれば電流は流れるはず・・・。
また電流がある程度以上の大きさになると、
イオンの量が足りなくなって、
流れにくくなるに違いありません・・・。
といった具合に、だんだん深みにはまっていくようです。
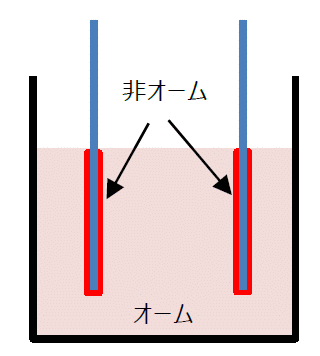
電極表面は、
オームの法則に従わない。
また正解の (c) を答えた人に、今度は「塩水の電気抵抗はいくら?」と聞いてみると、
はかばかしい答えが返ってきません。
(c) の挙動はオームの法則 V = RI に従っておらず(非オーム抵抗)、電圧が 0 V 付近では抵抗が極めて大きく、
電圧を上げていくにしたがって抵抗が急速に低下していくことになります。
ところで教科書には「イオンの独立移動の法則(コールラウシュ Kohlrausch の法則)」などというのが載っていて、
当量電気伝導度のデータなどが並んでいます。
どうなっているのでしょうか?
この話は、
この測定系が、電気分解の起きる、電極表面のオームの法則に従わない領域と、
その外部のオームの法則に従う領域からできていると考えてもらうとよいのです。
電極表面では電気の運び屋(電荷担体。キャリアー)が、電子からイオンに切り替わります。
こうしたキャリアーの切り替えには、
たいてい大きなエネルギーの出し入れをともなう過程をともない、
ここでは「化学反応」が起きます(発光ダイオード LED では光の放出)。
ネルンストの式で化学反応の起きやすさ(起電力)は評価できるわけですが、
反応速度は起電力に比例するほど単純ではありませんよね(つまりオームの法則に従わない)。
このオームの法則に従わない電極表面(だいたい 1 nm ぐらいの世界)の外部に、
オームの法則に従う世界が広がっているわけです。
そしてここでは、
電極表面の「化学」の世界とオームの法則の支配する均質な「物理」の世界、
その織りなす構図に目を向けようというわけです。
この実験では、まず電解質溶液の電気伝導度を測る上でのポイントを押さえ、
簡単な電気伝導度滴定に挑戦してもらいます。
そして用意してあるレポートシートを埋めて提出、
課題完了という手はずです。
テスターで塩水の電気抵抗を測るとどうなるか
お手軽な物理化学実験の教科書を見ると、
電解質溶液の電気伝導度の測定は、
白金電極に白金黒を付け(白金をツルツルではなく、雑にメッキする)、
ラジオの発信回路を使って抵抗を測るように指示してあります。
でも、なぜそうしないといけないかの説明はほとんどありません。
そのそもそものところを知ってもらうため、
この実験では、ちょっと知った人から見ると唖然とするようなことをやってもらっています。
でもこうした経験が、電気化学を理解する上で大事なのだと思っています。
中学・高校でイオンが電気を通す話を教わって、
さっそく塩水が電気を流すかどうか調べようというと、
まずテスターで測ってみようとするでしょう。
するとここで出会うような現象に出会って、
首をひねることになります。
テスターの抵抗測定モードで塩水にプローブを浸けると、
抵抗値がどんどん変化していきます。
使うテスター、プローブによって数 kΩ、数十 kΩ、あるいは数 MΩ という値も出るでしょう。
そこでしばらく置いて、
直流電圧測定モードにすると、これもテスターによって違いますが、
0.01 V ~ 1 V くらいの値が出て、だんだん減っていくでしょう。
最後マイナスの値で落ち着くことがあるかもしれません。
学生実験ではプローブ(電極)がステンレス線で、
使用するのが少し上等のマルチメーターと呼ばれる機種ですが、
たいてい抵抗値は数十 kΩ、発生する電圧が 0.5~1 V ぐらいになります。
小学校や中学校で、乾電池で豆電球が灯るかどうかで電気を流すかどうかを判断しますが、
豆電球の抵抗は10 Ωぐらいなものです。
この抵抗値を見ると、「塩水が電気を通す」というのは大嘘です。
でも塩水で感電したり、漏電したりというのも実際にある話。
どうなってるんでしょう?


|

|

|
|
電気伝導の電極と測定セル。
ここではビーカーにステンレス線で作った電極をテープで貼っている。
|
マルチメーター(デジタルテスター U1251A)で食塩水の電気抵抗をはかる。
抵抗値はだんだん大きくなり、この場合は 46 kΩ ぐらいになった。
|
電圧測定モードに切り替える。
1 V くらいの電圧が発生している。
電圧の値はだんだん小さくなっていく。
|
こうした現象が起きるのは、
そもそものテスターの仕組みに関わってきます。
通常のデジタルテスターの抵抗測定モードでは、
一定電流 I を流してその時の電圧 V の値から抵抗を V/I の関係から評価、表示します
(アナログテスターでは電圧一定で電流値をはかる)。
例えば学生実験で使用しているアジレント Agilent(現キーサイト Keysight)の U1251A では、
本文テキストにも書いたように、
50 kΩ レンジでは直流 41.2 µA 流す仕様になっています。
最初抵抗値が大きくなっていって、最終写真のように 46 kΩ を示したということは、
最初のうちは電圧が低くても 41.2 µA の電流が流れ、最終的に 1.9 V の電圧をかけて電気分解して、
41.2 µA 流れる状態に落ち着いたということなのです。
そしてこれを2次電池のように見立てれれば、
充電を止め電圧を測るモードに切り替えることで、
今度は放電の挙動を調べるようになるというわけです。
ですから実質、調べているのは電気分解。
たとえば入っている 0.01 mol/L 塩化ナトリウム溶液(0.06 %溶液)を、
飽和食塩水(26 %)に変えても同じような抵抗の挙動が現れます。
あるいは思い切って、水道水でも同じ挙動が見えるでしょう。
さすがにイオン交換水を入れると、数 MΩ あるいはそれ以上の抵抗値が出ます
(出ない時はイオン交換水を作るのに使っているイオン交換樹脂の性能が落ちていることがあるので、一報願いたいところです)。
なおこのテスターでの抵抗測定(=電気分解)で生成する電気分解生成物は、
非常に微量です。
10分はかり続けたとしても、直流 40 µA で流れる電気量は 0.024 C で、
ファラデー定数が105 C/mol ぐらいですから、
これで生成する電気分解生成物の物質量はせいぜい 2.5 × 10-7 mol 程度。
電極表面に少し色が付いたかどうかといったレベルです。
電極のステンレスの表面にできた、電池の活物質が何ものかも気になるところですが、
放電の電流は、1 V ぐらいの電圧で入力インピーダンスから、せいぜい 0.1 µA ですから、
この1/100 以下の問題になります。
同様に電極に付いたわずかの錆びや汚れも、その酸化還元反応で電池を構成することで、
この電圧には効いてきて、不安定な結果を与えます。
交流の利用
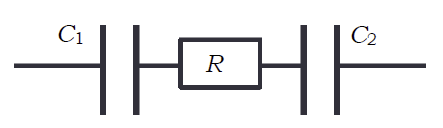
大胆に考えると、電圧が低い時はコンデンサーと抵抗の直列回路
さて、テスターでは塩水の電気抵抗がうまく測れないことを見たわけですが、
では電解質溶液の電気抵抗を知るにはどうすればいいのか?
すごく大胆に言えば、
塩水に電極を付けた回路は電圧が低く、電気分解がほとんど起きないような状態では、
右図のようなコンデンサ(キャパシタ)C1、C2 と抵抗 R の直列回路のようなものと見なしてもいいでしょう。
コンデンサは電極表面の領域に、抵抗は塩水に対応します。
テスターでは直流でこの回路を測ろうとしたので、高抵抗(高インピーダンス)で、
コンデンサの充電・放電に対応する挙動が見られたと思えばよいわけです。
ということは交流を使えば、インピーダンスは次式で与えられるので、
周波数 f を十分高くすれば抵抗が測れるでしょう
(C は合成容量 C1C2/(C1 + C2))。
\begin{equation}
Z = \sqrt{R^2 + \left( \frac{1}{2 \pi f C}\right)^2}
\label{eq:impedance}
\end{equation}
こうした大胆な簡易化が成立するかどうか、
実際にファンクションジェネレーターとオシロスコープをつないで、
周波数を変えてサイン波を通じた結果を下図に示します。
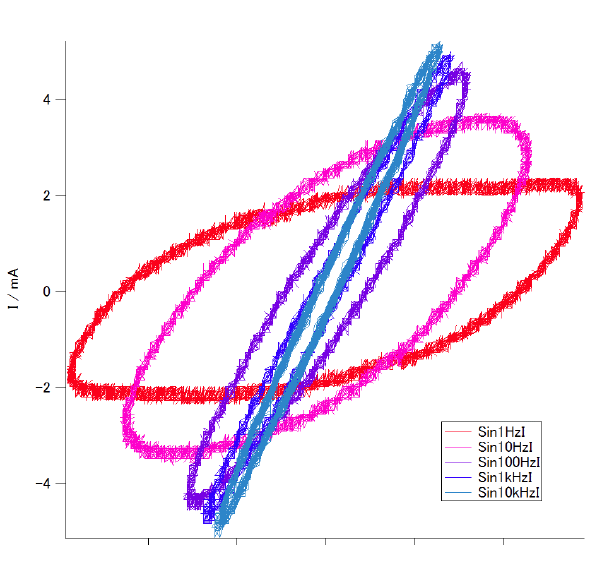
電圧・電流のリサージュ図形を書かせてみると、
手で電圧を上下させているような 1 Hz などという設定だと、
最初の(c) の図にあったような直流の電気分解に類似する挙動が見えていますが、
数十Hz 以上になると通常の RC 直列回路のように楕円の挙動になります。
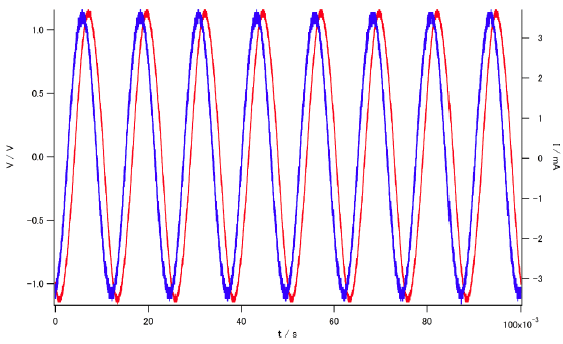
|
|
|
|
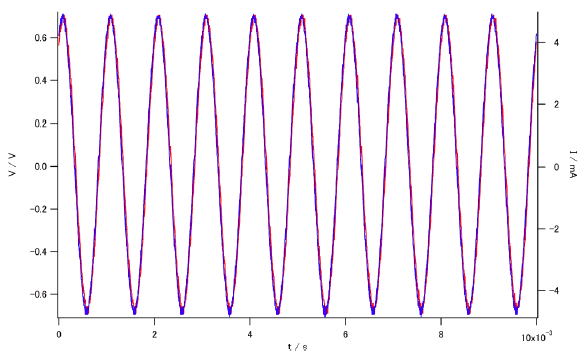
測定セルに 80 Hz のサイン波を通じた時の電圧(赤)と電流(青)の変化。
電流の位相が少し進んでいる。
|
測定セルに 1 kHz のサイン波を通じた時の電圧(赤)と電流(青)の変化。
位相のずれはほとんど見えない。
|
周波数を 1 Hz(赤)、10 Hz(桃)、100 Hz(薄紫)、1 kHz(紫)、10 kHz(青) と変えた、
リサージュ図形。
電圧・電流はそれぞれの軌道上を反時計回りに回る。
周波数を上げるにしたがって、オームの法則の挙動に近づく。
|
低周波数で見える挙動は溶液や電極の特性を色濃く反映し、
電極反応の「化学」として興味深く、
電気化学で話題に上るサイクリックボルタンメトリーといった手法は、
こうした現象を精密に取り扱うものになっています
(入門化学実験ではこうした課題を取り入れていたのですが、現在は省略しています)。
ここでは電極での挙動が通常の電気回路のコンデンサとして扱えるような周波数の高い領域を用い、
溶液の電気抵抗に注目しようというわけです。
電気伝導度滴定
精密な測定(~1 % 以上の精度)を行うには、まず電極をきちんと固定することは無論、
電極材料には化学的に安定なプラチナを用い、
表面積を大きくしてコンデンサーの容量を大きくする(白金黒を付ける)、
回路的には、周波数を変化させる、
容量成分を除くための工夫をする(ウィーンブリッジの利用)等々、
いろんなことが必要になってきます。
ここではともかく電解質溶液の電気伝導度の特徴を知るべく、
容易に利用できる 60 Hz の交流を用いて、
実際上も重要な電気伝導度滴定を題材に簡単な実験を行います。
まずどの程度の電気伝導度になるか調べてもらいます。
電極の大きさ、電極間距離いろいろですが、
典型的には電極でぐるぐる巻いた部分のおよその面積が 3 cm2 程度、
電極間距離が2 cm ぐらいなもの。
それで測った抵抗値は 0.01 mol/L の塩化ナトリウム溶液で、
だいたい 500 Ω ぐらいの値になります(20 %ぐらいは前後する)。
単純に計算すると (1/500 Ω) × 2 cm /3 cm2 で、
電気伝導度は 2 mS/cm 程度になります
(知名度があまり高くないようですが、S はジーメンスでコンダクタンスの SI 単位です)。
文献値は 1.18 mS/cm(25 °C)で、
いささか得られる伝導度は大きめ。
これは単純な対向電極として扱っているためで、
正しく評価するには電極・溶液全体の形状を考慮しないといけないのです
この種の問題はレポートシートの設問にも取り上げていますが、
理論的にはラプラス方程式を解く問題になります。
レポートシートの例は同心円筒型で話が簡単ですが、
2本の円筒型の電極の間の抵抗となると、
もう大変厄介な話になります。
実際問題として言えば、そもそも形状を正確に測定・評価するのは大変で、
仮に分かったとしてもラプラス方程式を解くのが困難です。
ですから実験的には、よく電気伝導度の知られた溶液(もっぱら塩化カリウム溶液)について測定し、
そした容器形状の効果は「セル定数」という形で評価することになります。
0.01 mol/L 溶液の電気伝導度(25 °C)
| G / mS cm-1 |
| HCl | 4.12 |
| NaOH | 2.38 |
| NaCl | 1.18 |
さて実験では0.008 mol/L ぐらいの塩酸に水酸化ナトリウム溶液を滴下して、
電気伝導度の変化を調べてもらいます。
すると本文テキストの実験例 にあるように、
当量点まで電気伝導度が減少、
そこから増加に転じるという V 字型の挙動が得られます。
こうしたいささか劇的な挙動が見られるのは、
右の表にあるように、塩酸・水酸化ナトリウムの電気伝導度が、
塩化ナトリウムに比べて格段に大きい、
あるいは水素イオン、水酸化物イオンの電気伝導度が格段に大きいためです
(このあたりはプロトンのバケツリレーが起きるという、
グロータス Grotthuss 機構として習うところ)。
塩酸に水酸化ナトリウムを加えていくと、当量点までは
HCl + NaOH → NaCl + H2O
の反応が進行します。
これは溶液中の塩酸を塩化ナトリウムに交換している、
水素イオンをナトリウムイオンに交換しているようなものです。
4.12 mS cm-1 の電気伝導度のものを
1.18 mS cm-1 のものと交換していくわけですから、
電気伝導度は下がります。
当量点以降は電気を通す水酸化ナトリウム(2.38 mS cm-1)を加えていくわけで、
電気伝導度が上がっていきます。
そしてその勾配の比は、およそ 2.38/(4.12 - 1.18) = 0.8 ぐらいになるというわけです
(水酸化ナトリウム溶液を加えたことによる希釈の効果を考慮する必要もありますが、
濃度が10倍くらい違い、そもそもの精度が10 %といったところですからあまり気にしなくてOK)。
電気伝導度の温度依存性
意外に教科書に登場しない話題に、
電解質溶液の電気伝導度の温度依存性があります。
これは机の上で考えているだけだと、
なかなか予想することが難しいようです。
レポートシートにある設問の学生諸君の予想もバラエティーに富んでいて、
温度を上げると分子衝突が激しくなって伝導度が下がるというのもあれば、
運動が激しくなって伝導度が上がるというのもあります。
講義で習う金属・半導体の電気伝導の話を思い出すと、
キャリアの数が変動するわけではないので、
温度を上げると伝導度が下がるという予想が多いようです。
まあ理屈はともかく、測ってみましょう。
ホットプレートスターラーは机に配置されているわけですから、
温度を上げる測定は容易だし、結果はすぐに確認できます。
やってみると、温度を上げると電気抵抗が減っていくこと、
電気伝導度が大きくなることが確認できます。
事実が確認できれば、
それを説明する理屈は絞られてきます。
もっとも単純な説明は、
「温度を上げると水の粘度が下がる」
というものでしょう。
溶液中のイオンに働く抵抗力は、
巨視的に見れば液体の粘度に比例すると考えられ、
水の粘度は温度を上げると減少します
(25 °C で 0.89 mPa s なのが 50 °C では 0.55 mPa s)。
これが温度を上げると塩水の電気伝導度が大きくなる理由だと言ってもまちがいではないでしょう。
ただしそれからさらに進んで、
「なぜ水の粘度が温度を上げると小さくなるのか」
という話になると(たぶん YY はそこまで考えないでしょうが・・・)、
後の気体の粘度の課題でも考えてもらうことになりますが、
話は単純ではなくなります。
また詳細に見ていくと、
電気伝導度の温度依存性は電解質によって異なり、
粘度の温度依存性と定量的には一致しません。
こうしたところから、
専門的な物理化学の研究は始まることになります。
いわば「大人の化学」の入り口に立つことになるわけです。
準備実験のページへ