|
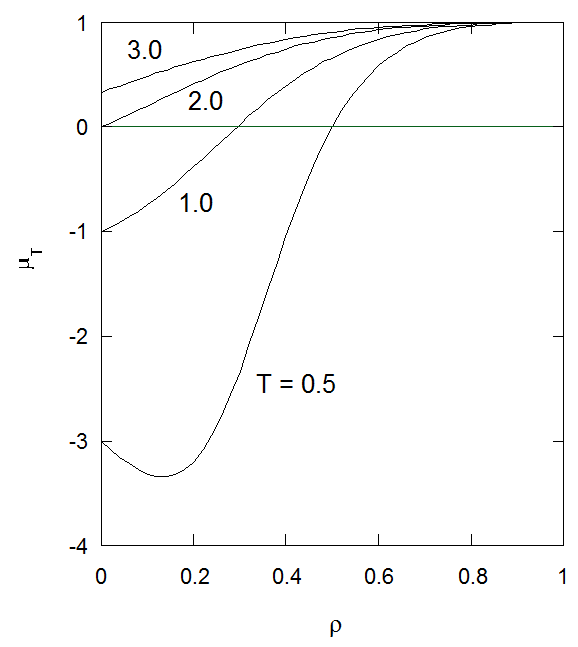
図3-1. 等温ジュール-トムソン係数\(\mu_{\rm{T}}\)の密度依存性。 等温ジュール-トムソン係数は、高密度の極限\(\rho \to 1\)では\(1 ~ [= b]\)になる。 |
圧力・温度・密度という立場から少し離れて、流体のエネルギーの観点からファンデルワールス状態方程式をみると、 また違う描像が見えてきます。
流体のエネルギーを考える時、まず注意しておきたいのは、内部エネルギーあるいはその温度微分である熱容量そのものの表現は、 \(P(\rho, T)\)という関係式からは出て来ないということです。 というのは一般的に内部エネルギー\(U\)についての関係式\(U(S, V, N)\)を考えると、 圧力はその体積に関する微分量です。 ですからある密度\(\rho_0\)を基準にとって、異なる密度の内部エネルギーを評価することはできても、 密度\(\rho_0\)におけるエネルギーの評価は守備範囲外なのです。 ここではモル内部エネルギー\(u = U/N\)が、 十分希薄で理想気体として扱える状態では、温度のみの関数\(u^{*}\)として扱えるものとして、 密度を変化させたときの相互作用エネルギーに着目します。
次のよく知られた内部エネルギーの体積微分(内部圧)の式から出発しましょう:
\begin{align} \pdifA{U}{V}{T,N} &= \pdifA{u}{v}{T} \\ &= \pdifA{u}{v}{s} + \pdifA{u}{s}{v} \pdifA{s}{v}{T} \\ &= -P + T \pdifA{P}{T}{v} \end{align}
ここからモル内部エネルギー\(u\)のモル体積\(v\)に対する微分量として次の式を得ます
\begin{equation} \left( \frac{\partial u}{\partial v} \right)_{T} = \rho^2 ~\left[ = a\rho^2 \right] \end{equation}
あるいはモル内部エネルギーの密度微分はもっと簡単です:
\begin{equation} \left( \frac{\partial u}{\partial \rho} \right)_{T} = -1 ~\left[ = -a \right] \end{equation}
ですから十分希薄な状態から積分することで、モル内部エネルギーの表現として次式を得ます。
\begin{equation} u = u^{*}(T) - \rho ~\left[ = u^{*}(T) - a\rho \right] \end{equation}
ここで\(u^{*}(T)\)は分子間相互作用の寄与を除いた内部エネルギーを意味し、 \(u^{*}(T)\) は分子の並進運動(“熱運動”)と分子内部のエネルギーに起因する要素からなることになります。 アルゴンなどの単原子分子では\((3/2)T ~[ = (3/2)RT ]\)で評価できます(電子励起等は無視)。 そして式によると、分子当たりの相互作用エネルギーは密度に比例し、元の状態方程式のパラメーターの\(a\)だけで決まり、 \(b\)には依存しないわけです。 このような簡単な形になることが、ファンデルワールス状態方程式の大きな特質といえるでしょう。 このことはそもそものファンデルワールス状態方程式の導出に当たって用いられた、 分子論的なモデルに起因しています。
ここで使用している単位系では、エネルギーの単位が\(ab^{-1}\)になっているので、 たとえば(4) 式は \(b a^{-1} u = b a^{-1} u^{*}(T) - b \rho\) の形になり、これを整理したものが(4) 式の[ ]内に入っている \(u = u^{*}(T) - a \rho\) の関係であることに注意ください。
今回の話ではファンデルワールス状態方程式の分子論な背景には基本触れないことにしていますが、 しばしば誤解があるようなので、少し説明を加えておきましょう。 ファンデルワールス状態方程式の基礎には、 「ある分子と周りの分子の間の引力的相互作用エネルギーの平均値は、 分子間引力の詳細に依存せず、周りに存在する分子の密度に比例する」 というアイデアがあるといってよいのです。 分子間引力としては“比較的”ゆっくり変化するものであれば構いません。 相互作用エネルギーが分子間距離の6乗に逆比例するようなロンドン分散力であってもよいし、 極性分子間に働く双極子相互作用のようなものでもいいのです。 ただ基本、2体力として扱えることは重要です。 たとえば3個の分子があって始めて現れるような相互作用をもっぱら考えるのであれば、 密度の2乗に比例するようなモル内部エネルギーを考えることになるでしょう。
モル内部エネルギーの表現から明らかですが、その密度一定での温度微分である定積モル熱容量\(c_V\)は、 温度が一定なら密度に依存しません。 こうした熱容量・比熱に関わる話題は、次章で取り上げるとして、 以下では初年級の熱力学でも、冷凍サイクルとの関わりで話題になる、ジュール-トムソン(ケルビン)効果について述べましょう。
ジュール-トムソン効果はエンタルピー\(H = U + PV\)が一定の条件下で、 流体の圧力変化に応じて温度が変化するという効果です。 つまり圧力\(P_0\)から\(P_1\)の状態に膨張した時、運動エネルギーを獲得するわけですが、 その運動エネルギーが熱に変わったらどうなるかという問題です。
流体力学で登場するベルヌイの式をご存じであれば、 単位体積当たりのエネルギーの保存から流線に沿って \(u + P/\rho + M c^{2} /2\) が一定になるわけですが(\(M\)はモル質量、\(c\)は流速)、 この運動エネルギー\(M c^{2} /2\)の項が熱となって失われ、 モルエンタルピー \(u + P/\rho = h\) の項に組み入れられると考えていただければよいでしょう。
ファンデルワールス流体のモルエンタルピーは次式で表わすことができます:
\begin{align} h &= u + Pv \\ &= u^{*}(T) + \frac{T}{1 - \rho} - 2 \rho \end{align}
ジュール-トムソン係数\(\mu_{\rm{JT}}\)は、 エンタルピー一定の条件での温度の圧力微分で定義されます。 簡単な計算で、ジュール-トムソン係数はモル定圧熱容量と、等温条件でのモルエンタルピー\(h = H/N\)の圧力微分とで表すことが示せ、 モルエンタルピーの圧力微分を等温ジュール-トムソン係数\(\mu_{\rm{T}}\)と呼びます(\(\mu_{\rm{JT}}\) と \(\mu_{\rm{T}}\)で符号が異なることに注意)。
\begin{align} \mu_{\rm{JT}} &= \pdifA{T}{P}{h} = - \pdifA{T}{h}{P} \pdifA{h}{P}{T} \\ &= - \frac{1}{c_{P}} \pdifA{h}{P}{T} = - \frac{1}{c_{P}} \mu_{\rm{T}} \end{align}
エンタルピーの圧力微分は、次のようにモル体積の温度依存性、等圧熱膨張率\(\alpha_{P}\)と関係づけられます。
\begin{align} \mu_{\rm{T}} &= \left( \frac{\partial h}{\partial P} \right)_{T} = \left( \frac{\partial h}{\partial P} \right)_{s} + \left( \frac{\partial h}{\partial s} \right)_{P} \left( \frac{\partial s}{\partial P} \right)_{T} \\ &= v - T \left( \frac{\partial v}{\partial T} \right)_{P} = v (1 - T \alpha_{P}) \end{align}
ファンデルワールス状態方程式についての等圧熱膨張率の表現を代入してあからさまに書くと、 次のような関係が得られます:
\begin{align} \mu_{\rm{T}} &= \frac{T - 2(1 - \rho)^2}{T - 2\rho(1 - \rho)^2} ~\left[ = \frac{bT - 2a(1 - b\rho)^2}{T - 2a\rho(1 - b\rho)^2} \right] \\ &= \frac{P - \rho(2 - 3\rho)}{P - \rho^2 (1 - 2\rho)} ~\left[ = \frac{bP - a \rho(2 - 3b\rho)}{P - a\rho^2 (1 - 2b\rho)} \right] \end{align}
先に見たように等圧熱膨張率\(\alpha_{P}\)はスピノーダル曲線上で発散するので、 等温ジュール-トムソン係数\(\mu_{\rm{T}}\)はスピノーダル曲線上で負に発散します (同時にモル等圧熱容量も発散し、 ジュールトムソン係数\(\mu_{\rm{JT}}\) (= \(-\mu_{\rm{T}}/c_{P}\))は発散せず、\((\partial T/\partial P)_{v}\)になります)。

|
図3-1. 等温ジュール-トムソン係数\(\mu_{\rm{T}}\)の密度依存性。 等温ジュール-トムソン係数は、高密度の極限\(\rho \to 1\)では\(1 ~ [= b]\)になる。 |
十分密度が低い状態では、等温ジュールトムソン係数 \(\mu_{\rm{T}}\) は\(1 - 2/T ~[ = b - 2a/RT ]\)で、 ジュールトムソン係数\(\mu_{\rm{JT}}\) (= \(-\mu_{\rm{T}}/c_{P}\))は低温(\(T \lt 2 ~[ =2a/bR ]\))で正(膨張とともに温度が下がる)、 高温(\(T \gt 2\))で負(膨張とともに温度が上がる)となります。 また密度を大きくするにつれ、等温ジュールトムソン係数\(\mu_{\rm{T}}\)は大きくなり、\(\rho \to 1\)で1になります。 ジュールトムソン係数が符号を変える境界線、いわゆる反転曲線は、 \(PT\)面では次の密度によるパラメーター表示で与えられます:
\begin{align} T_{\rm{inv}} &= 2 (1 - \rho)^2 ~\left[ = \frac{2a}{b} (1 - b \rho)^2 \right] \\ P_{\rm{inv}} &= \rho (2 - 3\rho) ~\left[ = \frac{a}{b} \rho (2 - 3b\rho) \right] \end{align}
|
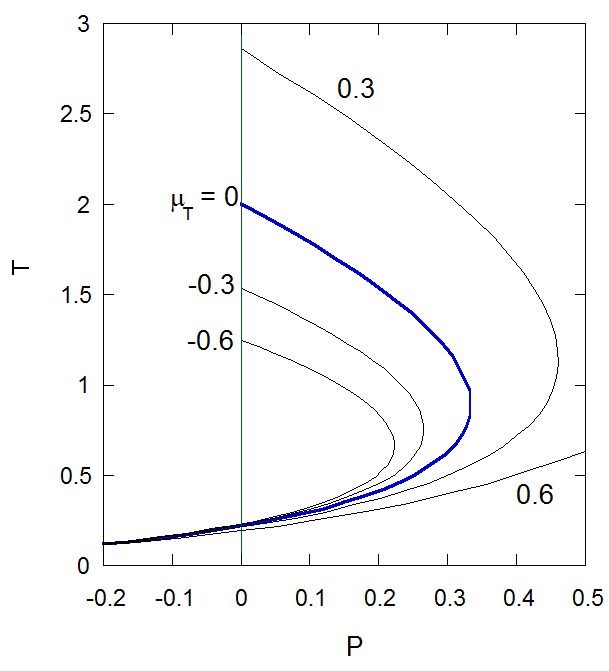
図3-2. 等温ジュール-トムソン係数\(\mu_{\rm{T}}\)の\(PT\)面における挙動。 青い実線が\(\mu_{\rm{T}} = 0\)となる反転曲線。 これを境に高圧側では等エンタルピー的な膨張にともない温度が上昇する。 \(T \gt 2\)では常に等温ジュール-トムソン係数は正\(\mu_{\rm{T}} \gt 0\)で、 ジュール-トムソン係数は負になる\(\mu_{\rm{JT}} \lt 0\) (膨張にともない温度が上がる)。 |
この反転曲線でもっとも圧力が高くなるのは密度が\(\rho_{\rm{inv}} ({\rm{max}}) = 1/3\)で、 圧力\(P_{\rm{inv}} ({\rm{max}}) = 1/3\)、温度は\(T_{\rm{inv}} ({\rm{max}}) = 8/9\)。 密度はちょうど臨界密度、\(P_{\rm{inv}} ({\rm{max}})\)は臨界圧力の9倍、 \(T_{\rm{inv}} ({\rm{max}})\)は臨界温度の3倍にあたります。