|
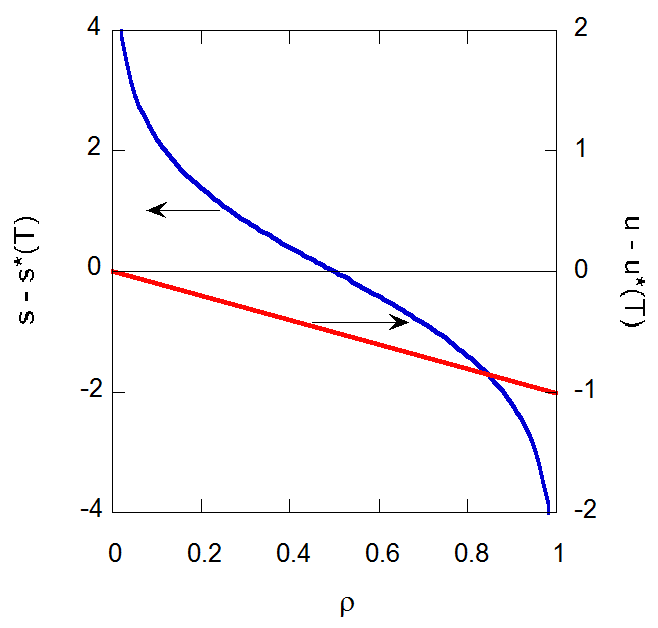
図4-1. 配置のモルエントロピー\(s - s^{*} (T)\)とモル内部エネルギー\(u - u^{*} (T)\)の密度依存性。 エントロピーは\(\rho = 0.5\)を中心に対称的な挙動を示す。 |
状態方程式からエネルギーと温度\(T\)圧力\(P\)密度\(\rho\) に関わる関係を見たわけですが、 ここでエントロピー、そしてその温度微分として熱容量・比熱を取り上げましょう。 エネルギーの議論でも出てきましたが、 状態方程式\(P(T, \rho)\)からはエントロピーそのものの温度依存性の表現は出て来ません。 ですからある密度\(\rho_0\)を基準にとって、異なる密度のエントロピーを評価する形をとることになります。
次のモルエントロピー\(s = S/N\)のモル体積\(v = V/N\)による微分の式から出発しましょう:
\begin{equation} \pdifA{s}{v}{T} = \pdifA{P}{T}{v} \end{equation}
ファンデルワールス状態方程式の圧力温度係数\(\partial P/\partial T\)は、モル体積のみの関数で書けます。
\begin{equation} \left( \frac{\partial s}{\partial v} \right)_{T} = \frac{1}{v - 1} \end{equation}
これを積分することで次式を得ます
\begin{align} s &= s^{*} (T) + \ln (v - 1) = s^{*} (T) - \ln \frac{\rho}{1 - \rho} \label{eq:entropy} \\ & \left[ = s^{*} (T) + R \ln \frac{v - b}{b} = s^{*} (T) + R\ln \frac{1 - b\rho}{b \rho} \right] \end{align}
ここで \(s^{*}(T)\) はモルエントロピーの密度依存しない項で、 ある基準となる密度 \(\rho_0\) におけるモルエントロピーを意味します。 先に見た内部エネルギーの時の扱いとそろえるために、 基準となる密度 \(\rho_0\) を十分小さくとることにすると、 内部エネルギーの場合同様、\(s^{*}(T)\) には分子間相互作用によらない、 分子の並進運動や分子内部構造に起因する要素が詰まっていると考えていただければよいでしょう。 このエントロピーの密度依存する部分\(s - s^{*}(T)\) をここでは配置のエントロピー configurational entropyと呼ぶことにします。
この密度に依存しないエントロピーの項 \(s^{*}(T)\) の取り方には任意性があることには注意が必要です。 基準となる密度 \(\rho_0\) を十分小さくとるというわけですが、 どれぐらい小さくとるかは任意です(例えば \(10^{-11}\) でも \(10^{-20}\) でもかまわない )。 内部エネルギーを考えた時には、十分希薄な状態では相互作用エネルギーが 0 になるという前提があったので取り扱いは容易だったのですが、 モルエントロピーの場合には密度小さくするにしたがって発散してしまいます。 結局のところ \(\partial s^{*}(T)/\partial \rho = 0\) ということだけを約束しているわけで、 例えば配置のエントロピーを \(T + \ln(v - 1)\) として、新たに \(s^{*}(T) - T \) を密度に依存しないエントロピーの項としてもいいわけです。 あるいはここでは元のファンデルワールス状態方程式のパラメーター \(b\) を配置のエントロピーに含めて考えていますが、 それを \(s^{*}(T)\) に持ち込んでもいいのです。
こうした問題があったりするので、理想気体状態を基準にとって表現することも行われます。 つまり同じ温度で理想気体のようにふるまうと考えた時の、 密度 \(\rho\) でのエントロピー \(s_{\rm{ideal}}\) を用いて次のように表すわけです:
\begin{align} s_{\rm{ex}} &= s - s_{\rm{ideal}} \\ &= \int_{0}^{\rho} {\left[ \pdif{s}{v} - \pdifA{s}{v}{\rm{ideal}} \right]} \frac{\rmd v}{\rmd \rho} \rmd \rho \\ &= -\int_{0}^{\rho} {\left( \frac{1}{\rho (1 - \rho)} - \frac{1}{\rho} \right)} \rmd \rho \\ &= \ln (1 - \rho) ~ \left[ = R \ln (1 - b\rho) \right] \end{align}
この \(s_{\rm{ex}}\) を過剰エントロピーexcess entropyと呼びます (残余エントロピーresidual entropyとも呼ばれますが、第3法則との関係で呼ばれるものとは別物なので注意)。 一般的な過剰量の表式を書いておくと次のようになります:
\begin{equation} X_{\rm{ex}} (\rho) = \int_{0}^{\rho} {\left[ \pdifA{X}{\rho}{T} - \pdifA{X}{\rho}{T, \rm{ideal}} \right]} \rmd \rho \end{equation}
この表記は密度に依存しない項の設定にあいまいさがなく、 分子間相互作用に基づく寄与を示すうえでも有効です。 けれども今回のお話しでは頻繁に密度微分を取ったりするので、 常に理想気体の項の寄与を考慮する必要がありかえって流れを見えにくくすると思うので、 ここでの話ではあらわな形で密度依存性を表記することにし、 密度に依存しないエントロピーの項 \(s^{*}(T)\) は先に示した式 \eqref{eq:entropy} で定義することにします。
式 \eqref{eq:entropy} のエントロピーの表現で重要なのは、エントロピーの密度依存性に関わって、 内部エネルギー同様、温度依存性を持たないことです (圧力一定で考えると、密度の温度依存性を介して温度依存性が現れます)。 ただし内部エネルギーの時とはちがって、 元のファンデルワールス状態方程式でいうと\(a\)パラメーターには依存せず、 \(b\)パラメーターに依存する形です。 元の状態方程式の温度に比例する\(b\)パラメーターを含む項はエントロピー、 温度に依存しない\(a\)パラメーターを含む項は内部エネルギーを反映している、 と整理してもいいでしょう。
内部エネルギーもエントロピーも、その密度依存性については温度によらず、 それぞれのようすを図にすると次のようになります:

|
図4-1. 配置のモルエントロピー\(s - s^{*} (T)\)とモル内部エネルギー\(u - u^{*} (T)\)の密度依存性。 エントロピーは\(\rho = 0.5\)を中心に対称的な挙動を示す。 |
さてこのファンデルワールス流体のエントロピーの表現の重要な特徴は、 その密度依存性が温度に依存しないことです。 ですからモル定容熱容量\(c_v\)は密度によらず一定です:
\begin{equation} c_{v} = T \pdifA{s}{T}{v} = T \pdifA{s^{*} (T)}{T}{v} = c^{*}_{v} (T) \end{equation}
一方モル定圧熱容量\(c_P\)は密度依存性を持ち、次のように表わされます
\begin{align} c_{P} &= T \pdifA{s}{T}{P} \\ &= T \pdifA{s}{T}{v} + T \pdifA{s}{v}{T} \pdifA{v}{T}{P} \\ &= c_{v} - T \left[ {\pdifA{P}{T}{v}} \right] ^{2} \pdifA{v}{P}{T} \\ &= c_{v} + T [f(\rho)]^2 \frac{1}{\rho^2 [T f'(\rho) - 2\rho]} \\ &= c_{v} + \frac{T}{T - 2\rho (1 - \rho)^2} ~ \left[ = c_{V} + \frac{RT}{T - 2a\rho (1 - b\rho)^2} \right] \end{align}
相が安定であるなら(機械的不安定性を示さない \(\partial v/ \partial P \lt 0\)なら)\(c_P \gt c_v\)です。
|
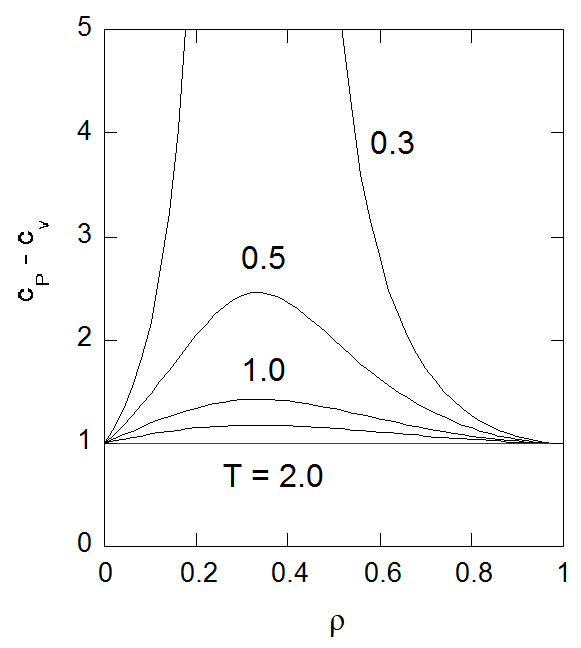
図4-2. モル定圧熱容量\(c_P\)の密度依存性。 図には密度依存しないモル定積熱容量\(c_v = c^{*}_{v} (T)\)との差の形で表示してある。 |
十分密度が低い状態では、モル定圧熱容量\(c_P\)は次式で与えられ、 密度\(\rho \to 0\)の理想気体状態では\(c_V + 1 ~[ = c_V + R] \)で(マイヤーMayerの関係)、 密度を上げるにしたがって最初増加します。
\begin{equation} c_{P} \approx c_V + 1 + \frac{2}{T} \rho ~\left[ = c_V + R(1 + \frac{2a}{T} \rho) \right] \end{equation}
そして\(\rho = 1/3\)(臨界密度)で最大値\(c_{P}({\rm{max}})\)を取り、 その後減少に転じることになります。
\begin{align} c_{P}({\rm{max}}) &= c_{V} + \frac{T}{T - 8/27} \\ &= c_{V} + \frac{T}{T - T_{\rm{c}}} ~ \left[ = c_{V} + \frac{RT}{T - T_{\rm{c}}} \right] \end{align}
常温常圧の液体(臨界密度以上の液体です)の定圧比熱は圧力を上げると一般に小さくなります。 このことは圧力一定でのモル体積の温度依存性が下に凸の曲線になることと等価です。
\begin{align} \left( \frac{\partial c_{P}}{\partial P} \right)_{T} &= \left( \frac{\partial}{\partial P} T \left( \frac{\partial s}{\partial T} \right)_{P} \right)_{T} \\ &= T \left( \frac{\partial}{\partial T} \left( \frac{\partial s}{\partial P} \right)_{T} \right)_{P} \\ &= -T \left( \frac{\partial}{\partial T} \left( \frac{\partial v}{\partial T} \right)_{P} \right)_{P} = -T \left( \frac{\partial^2 v}{\partial T^2} \right)_{P} \end{align}
実際、常圧下での液体の比容の温度依存性は(ぼくの知る限り低温でのメタノールの挙動を除くと)下に凸になり、 これは水も例外ではありません。 ファンデルワールス状態方程式で、こうした実在流体の膨張挙動が再現できているといっていいでしょう。 ただし実験的には、さらに圧力を上げると(通常100 MPa程度)、 一般に比熱が圧力とともに増加する(体積の温度依存性が上に凸になる)ようになるのですが (P. W. Bridgman, “The Physics of High Pressure,” Chap. 5, Dover 1970 (原著は1931年の出版))、 これはファンデルワールス状態方程式では説明できません。
エントロピーの表現が得られたので、 いわゆる断熱可逆過程(等エントロピー過程)の変化量についても見通しが得られます。 温度が変化するので正確な評価にはモル定容熱容量\(c_V\)の温度依存性についての知見が必要になるのですが、 これ以降では、考えている温度領域で、温度によらず\(c_V\)は一定であるとします(通常単原子気体では\(c_V = 3/2 ~[ = (3/2)R] \)です)。 するとエントロピーの温度・密度依存性の表式として、ある温度\(T_0\)を基準にとって次式が得られます:
\begin{equation} s = s^{*}(T_0) + c_V \ln \frac{T}{T_0} + \ln (v - 1) \end{equation}
したがってエントロピー一定の条件下では、温度・モル体積の間には次の関係が成り立ちます:
\begin{equation} c_V \ln T + \ln (v - 1) = \rm{const} \end{equation}
理想気体の場合によく用いられる表現\(T v^{1/c_V} = \rm{const}\)との対応でいうと、 次のような表現になります:
\begin{equation} T (v - 1)^{1/c_V} ~\left[ = T (v - b)^{R/c_V} \right] ~ = \rm{const} \end{equation}
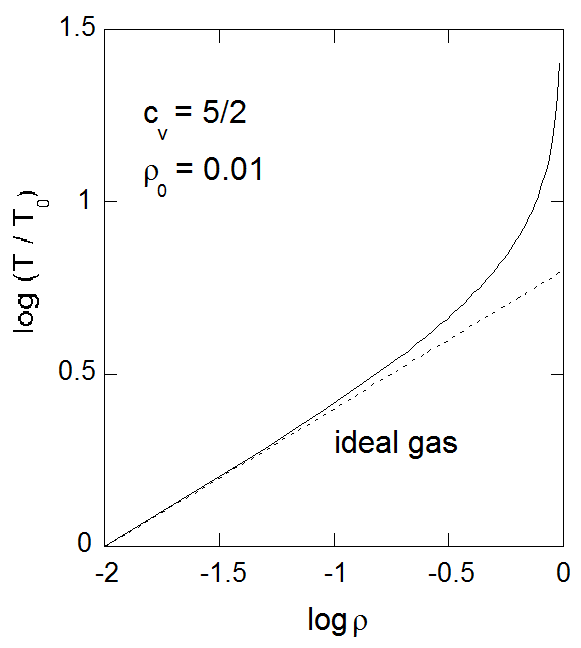
図4-3にも見るように、圧縮にともないファンデルワールス流体は、理想気体と見なした時より高温になります。 このような簡単な関係が得られるのは、断熱条件下でのモル体積の温度微分が、 次のようにモル体積のエントロピー微分、圧力の温度微分と対応付けられるところからもあきらかです。
\begin{align} \pdifA{v}{T}{s} &= -\pdifA{v}{s}{T} \pdifA{s}{T}{v} \\ &= -\pdifA{T}{P}{v} \frac{c_v}{T} = - \frac{v-1}{T} c_v \end{align}
断熱圧縮において、密度に注目する限り、 到達温度には元の状態方程式の\(a\)パラメーターは無関係であることは注意しておいてよいでしょう。
|
図4-3. 断熱可逆圧縮における温度の密度依存性。 図では定積熱容量\(c_v = 5/2\)(2原子分子相当)の流体を、 初期状態で密度\(\rho = 0.01\)から断熱可逆圧縮した場合の、 初期温度\(T_0\)からの温度上昇を示してある。 |
この一方で断熱条件下の温度と圧力、あるいは圧力とモル体積の関係は、 等圧比熱の密度依存性が単純なふるまいをしないことからも明らかに、 一筋縄ではいきません。たとえば断熱条件の圧力変化にともなう温度上昇は、次式のように等圧熱膨張率\(\alpha_P\)と関係づけられ
\begin{equation} \pdifA{T}{P}{s} = -\pdifA{T}{s}{P} \pdifA{s}{P}{T} = \frac{T}{c_P} \pdifA{v}{T}{P} = \frac{vT}{c_P} \alpha_P \end{equation}
ジュールトムソン係数
\begin{equation} \mu_{\rm{JT}} = \pdifA{T}{P}{h} = - \frac{1}{c_P} \mu_{\rm{T}} = \frac{v}{c_P} (T \alpha_P - 1) \end{equation}
より大きくなるところまではいいのですが、 あらわな形で断熱条件下での\(TP\)の関係を記述するのは、 ジュール-トムソン効果と同様にやっかいで、密度\(\rho\)を介したパラメーター表示の形にするのが無難でしょう。
|
|
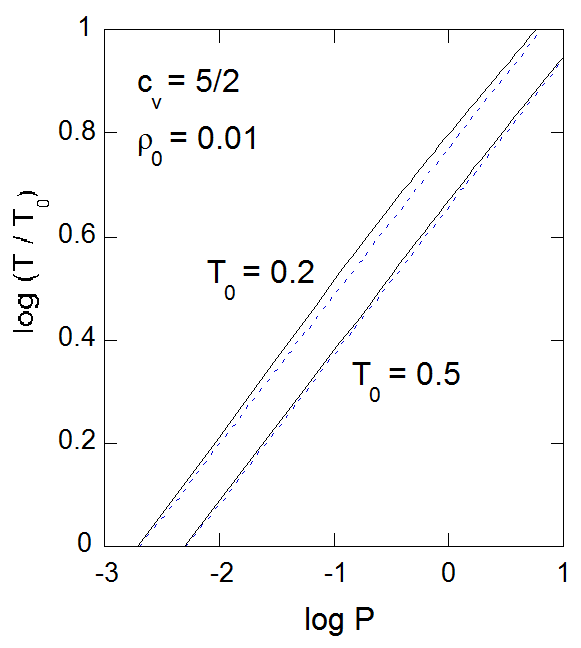
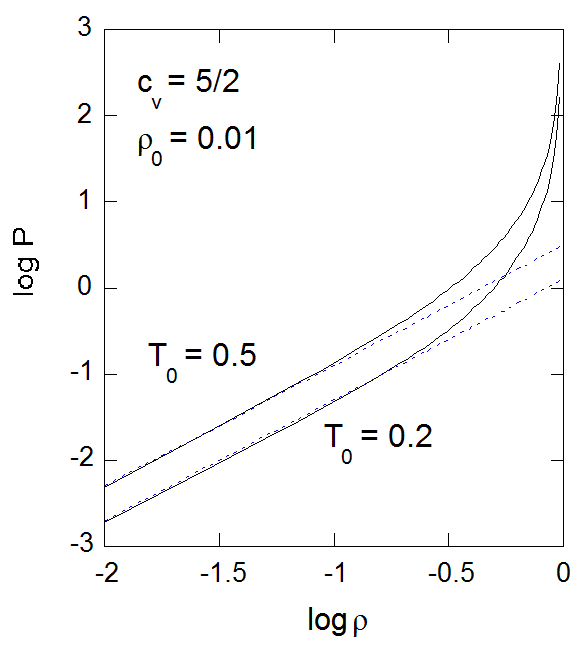
| 図4-4. 断熱圧縮における温度の圧力依存性。 図では定積熱容量 \(c_v = 5/2\)(2原子分子相当)の流体を、 初期状態で密度 \(\rho = 0.01\) から断熱可逆圧縮した場合の温度上昇を、 初期温度 \(T_{0} = 0.2\) と \(T_{0} = 0.5\) の場合について示してある。 | 図4-5. 断熱圧縮における圧力の密度依存性。 図4-4と同じく、定積熱容量\(c_v = 5/2\)(2原子分子相当)の流体を、 初期状態で密度\(\rho = 0.01\)から断熱可逆圧縮した場合の温度上昇を、 初期温度 \(T_{0} = 0.2\) と \(0.5\) の場合について示してある。 |
図4-4には圧力に対する温度の変化の様子を示しました。 概ね理想気体の振舞いに近いものの、若干、到達温度は高めになります。 圧縮した時の圧力については、図4-5に示すように、低密度側で少し低めになることがありますが、 高密度側で高く振れます。
断熱圧縮率は音速\(c\)と密接に関わります。 音速cはモル質量を\(M\)とすると次式で表されます(ニュートン-ラプラスNewton-Laplaceの式):
\begin{align} M c^{2} &= \pdifA{P}{\rho}{s} = -\pdifA{P}{s}{\rho} \pdifA{s}{\rho}{P} = -\pdifA{P}{T}{\rho} \pdifA{T}{s}{\rho} \pdifA{s}{T}{\rho} \pdifA{T}{\rho}{P} \\ &= \frac{c_P}{c_v} \pdifA{P}{\rho}{T} \end{align}
ここで定圧熱容量に関する表式を用いると
\begin{align} M c^{2} &= \pdifA{P}{\rho}{T} + \frac{T}{c_{v} \rho^{2}} \left[ \pdifA{P}{T}{v} \right]^{2} \label{eq:soundspeed}\\ &= T f'(\rho) - 2 \rho + \frac{T}{c_{v} \rho^{2}} f(\rho)^{2} \\ &= \frac{1 + c_v} {c_v} \frac{T}{(1 - \rho)^2} - 2 \rho \end{align}
|
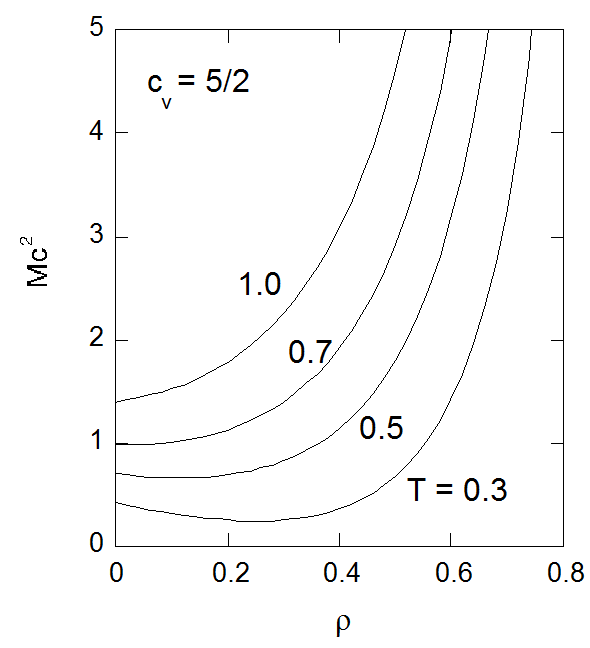
図4-6. 種々の温度における音速の密度依存性。 図では定積熱容量 \(c_v = 5/2\)(2原子分子相当)とした結果を示してある。 |
音速は低密度において\(T \gt c_v/(1+c_v)\) なら密度を上げると単調に増大します。 この一方\(T \lt (c_v /(1+cv)\)なら密度を上げると最初減少し、 それから増加するという挙動を示します。 なおファンデルワールス状態方程式からは、 等温圧縮率が発散するスピノーダル曲線上あるいは臨界点において音速は0になったり発散したりしません。 スピノーダル曲線上の音速 \(c_{\rm{sn}}\) は次式で与えられます (式 \eqref{eq:soundspeed} で\(\partial P/\partial \rho = 0\)になることに注意します)。
\begin{equation} M c_{\rm{sn}}^2 = \frac{T}{c_v (1 - \rho)^2} \end{equation}
特に臨界点における音速\(c_{\rm{c}}\)は次のようになります
\begin{equation} M c_{\rm{c}}^2 = \frac{2}{3 c_v} \end{equation}