|
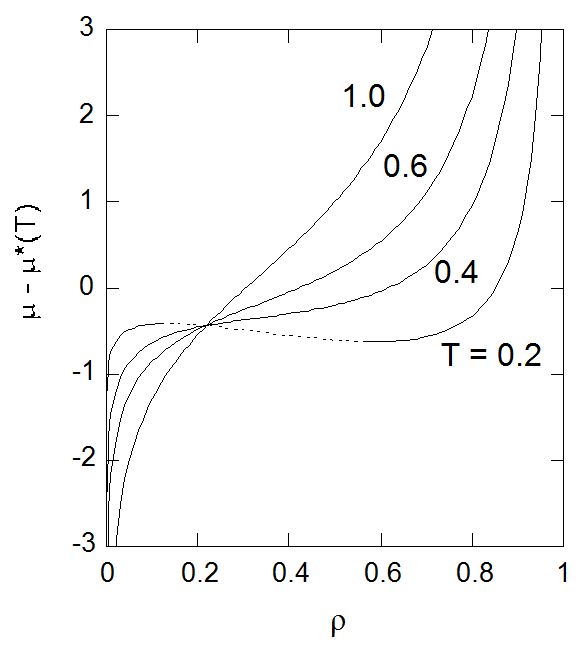
図5-1. 化学ポテンシャルの密度依存性。 \(T = 0.2\) では物質不安定性が現れる(点線部分)。 |
エネルギー、エントロピーと見てきて、ここでは化学ポテンシャル、 そして自由エネルギーなどについて見てみることにしましょう。 一成分系で均一相を扱う限りにおいては、系の加成性から、 化学ポテンシャルをことさらに取り上げる必要はないという考えも可能です。 けれども二相共存領域を扱う上では化学ポテンシャルの問題は避けて通れません。 また何より多成分系への適用を考える上で、その表式を得ておくことは重要です。
化学ポテンシャルについても、状態方程式\(P(T, \rho)\)からは、 化学ポテンシャルそのものの温度依存性の表現は出て来ないので、 ある基準となる状態の密度\(\rho_0\)における化学ポテンシャルを考えて、 評価する形をとることになります。 ギブズ-デュエムの関係から導かれる、次の化学ポテンシャルの圧力微分の式から出発しましょう:
\begin{equation} \pdifA{\mu}{P}{T} = v \end{equation}
ここから化学ポテンシャルの表式として次の式を得ます。
\begin{align} \mu &= \mu(T, \rho_0) + \int^{P}_{P_0} {v \rmd P} \\ &= \mu(T, \rho_0) + \left[ Pv \right]^{P}_{P_0} - \int^{v}_{v_0} {P \rmd v} \\ &= \mu(T, \rho_0) + Pv - P_{0}v_{0} - \int^{v}_{v_0} \left( \frac{T}{v - 1} - \frac{1}{v^2} \right) {\rmd v} \\ &= \mu^{*}(T) + \frac{vT}{v - 1} - T \ln (v - 1) - \frac{2}{v} \\ &= \mu^{*}(T) + \frac{T}{1 - \rho} + T \ln \frac{\rho}{1 - \rho} - 2 \rho ~ \left[ = \mu^{*}(T) + \frac{RT}{1 - b \rho} + RT \ln \frac{b\rho}{1 - b\rho} - 2 a \rho \right ] \end{align}
ここで \(\mu^{*}(T)\) は、エントロピーの表式の場合と同様、 化学ポテンシャルから密度依存の項を除いたものに相当しています。 この表式は、すでに得ているモル内部エネルギーとモルエントロピーの表式から与えられるものと合致します:
\begin{align} \mu &= u + P/\rho - Ts \\ &= u^{*}(T) - \rho + \frac{T}{1 - \rho} - \rho - T \left[ s^{*}(T) - \ln \frac{\rho}{1 - \rho} \right] \\ &= [u^{*}(T) - Ts^{*}(T)] + \frac{T}{1 - \rho} + T \ln \frac{\rho}{1 - \rho} - 2\rho \end{align}
化学ポテンシャルの密度微分は、次のように圧力の密度微分と対応付けられます:
\begin{equation} \pdifA{\mu}{\rho}{T} = \pdifA{\mu}{P}{T} \pdifA{P}{\rho}{T} = v \pdifA{P}{\rho}{T} \label{eq:dmudd} \end{equation}
この関係を用いて、過剰化学ポテンシャル \(\mu_{\rm{ex}}\) は次のように与えられます:
\begin{align} \mu_{\rm{ex}} &= \int_{0}^{\rho} {\left[ \pdifA{\mu}{\rho}{T} - \pdifA{\mu}{\rho}{T, \rm{ideal}} \right]} \rmd \rho \\ &= \int_{0}^{\rho} {\left[ v \pdifA{P}{\rho}{T} - v \pdifA{P}{\rho}{T, \rm{ideal}} \right]} \rmd \rho \\ &= \int_{0}^{\rho} {\left[ \frac{T}{(1- \rho)^2} + \frac{T}{1- \rho} - 2 \right]} \rmd \rho \\ &= \frac{\rho T}{1 - \rho} - T \ln (1 - \rho) - 2 \rho \label{eq:muex} \end{align}
図5-1 には、化学ポテンシャルの密度依存性を示しました。 化学ポテンシャルの密度微分が圧力の密度微分と対応付けられる(式 \eqref{eq:dmudd})ことからも明らかに、 化学ポテンシャルも圧力の場合と同様に、低温で密度とともに化学ポテンシャルが減少する不安定領域が現れ、 その領域は機械的な不安定性を示す領域と一致します。

|
図5-1. 化学ポテンシャルの密度依存性。 \(T = 0.2\) では物質不安定性が現れる(点線部分)。 |
ただしその不安定性のありようは少し違っています。 機械的な不安定性の時には体積の変化を考えたのですが、化学ポテンシャルに基づく不安定性では物質の移動が基本になります。 つまり \(\partial \mu /\partial \rho \lt 0\) であれば、ある領域の密度がほんの少し周りより高くなった時、 化学ポテンシャルが周りより下がってしまいます。 すると化学ポテンシャルのつり合いが崩れて、周りから流体が流れ込み、 さらに密度が上がり化学ポテンシャルが下がる(周りでは逆の現象が起きる)。 こうしたプロセスが密度の増加にともない化学ポテンシャルが増加する状態に達するまで続き、 気液の相分離に至るわけです。 このように化学ポテンシャルのつり合いに関わって相が不安定になる挙動を、 物質不安定性 material instability あるいは拡散的な不安定性 diffusive instability と呼びます。
こうした機械的不安定性と物質不安定性のシナリオのちがいは、一見どうでもよいことのように思われるかもしれません。 体積が増減しても、物質が流入・流出しても、結果的には密度の変化が起きるには違いがありません。 式 \eqref{eq:dmudd} はまさにこのことを示しています。 しかし話を多成分系に拡張すると単純ではありません。 例えば水に少量のエーテルが溶け込んだ状態を考えと、体積が一定であっても水が流入しエーテルが流出することで、 機械的な不安定性は起きずに物質不安定性は起きうるわけです。 ですからこのあたりの記述には、少し意を用いてほしいところなのです。
さてファンデルワールス流体の配置の化学ポテンシャルの重要な特徴は、 圧力と同様、温度に比例する項と密度のみに依存する項の和で表されていることです。
\begin{equation} \mu - \mu^{*}(T) = T \left[ \frac{\rho}{1 - \rho} + \ln \frac{\rho}{1 - \rho} \right] - 2\rho \end{equation}
ここで興味深いのは \(T\) に比例する項が、\(\rho = 0.2178 \ldots\) の時に0になり、 \(\mu - \mu^{*}(T)\) の値は温度依存性を失い \(-0.4356 \ldots\) で一定になることです。 次の関係に注意すると
\begin{equation} \pdifA{\mu}{T}{\rho} = \pdifA{\mu}{T}{P} + \pdifA{\mu}{P}{T} \pdifA{P}{T}{\rho} = -s + v \pdifA{P}{T}{\rho} = -s + \frac{\rho}{1 - \rho} \end{equation}
エントロピーの密度依存の項は \(\rho = 0.5\) でゼロになるわけですが、 化学ポテンシャルでは温度依存の項がエントロピーにのみ依っているわけではないので挙動が変わってきます。
なお化学ポテンシャルと深くかかわる量として、最近の物理化学の教科書では登場する機会が減っているようですが、 逃散能(フガシティー fugacity)があります。 逃散能 \(f\) は通常、十分希薄な状態で圧力と等しくなるように取り、次のように定義されます:
\begin{equation} f = P^{\circ} \exp \left( \frac{\mu - \mu^{\circ}}{T} \right) \label{eq:fugacity} \end{equation}
ここで上付き \(\circ\) を付けたのは基準に取る状態の熱力学量(通常圧力 1 bar あるいは1 atm の状態が取られます)で、 流体が理想気体として振舞うとして評価されるものです。 先の過剰化学ポテンシャルを用いれば、次の関係に注意して
\begin{align} \mu_{\rm{ex}} &= \mu - \mu_{\rm{ideal}} \\ &= \mu - [\mu^{*}(T) + T \ln \rho ] \\ &= \mu - [\mu^{\circ} + T \ln \frac{\rho}{\rho^{\circ}}] \\ \end{align}
式\eqref{eq:fugacity} は次のように書けます(\(P^{\circ} = \rho^{\circ} T\) に注意):
\begin{align} f &= P^{\circ} \frac{\rho}{\rho^{\circ}} \exp \left( \frac{\mu_{\rm{ex}}}{T} \right) \\ &= \rho T \exp \left( \frac{\mu_{\rm{ex}}}{T} \right) \end{align}
逃散能は、今日、理学部で物理化学を学ぶ文脈では、活動度(活量)activity と呼んだ方が通りがいいかもしれません。 先の過剰化学ポテンシャルの表現、式 \eqref{eq:muex}を用いると、 ファンデルワールス流体の逃散能は
\begin{equation} f = \frac{\rho T}{1 - \rho} \exp \left( \frac{\rho}{1 - \rho} - \frac{2\rho}{T} \right) \end{equation}
あるいはよく用いられるフガシティー係数 \(\phi = f/P\) の形で書けば
\begin{equation} \ln \frac{f}{P} = \frac{\rho}{1 - \rho} - \frac{2\rho}{T} - \ln \left[ 1 - \frac{\rho (1 - \rho)}{T} \right] \end{equation}
のように表されることになります。
自由エネルギーは物理化学でよく言及されますが、実のところ言うと、 物理化学での自由エネルギーは、 第2法則から平衡条件を与えるのに登場するものの(例えば \(TVN\) 一定の条件で、ヘルムホルツエネルギーが最小となる)、 自由エネルギーそれ自体が観測の対象になることはほとんどなく、 もっぱら種々の熱力学量を導出したりするのに登場し、 いわば「黒幕」と言ってもいいでしょう。 直接的に自由エネルギーが関心事となるのは、最大仕事といった、 どちらかというと工学的な用途(こういう文脈ではエクセルギーexergyという形で語られます)と言えるかもしれません。 ここではファンデルワールス状態方程式から導かれる、 この「黒幕」の構成について簡単に触れるにとどめます。
モルギブズエネルギーは化学ポテンシャルに等しいので、特に触れるまでもないでしょう。 モルヘルムホルツエネルギー \(\alpha = A/N\) は、モル体積による微分が圧力です:
\begin{equation} \pdifA{\alpha}{v}{T} = -P \end{equation}
ですからこれを基準となる密度から積分することで、 モルヘルムホルツエネルギーの表現が次のように得られます
\begin{align} \alpha &= \alpha(T, v_0) - \int^{v}_{v_0} {P {\rm{d}} v} \\ &= \alpha(T, v_0) - \left[ T \ln (v - 1) + \frac{1}{v} \right]^{v}_{v_0} \\ &= \alpha^{*}(T) - T \ln (v - 1) - \frac{1}{v} = \alpha^{*}(T) - T \ln \frac{\rho}{1 - \rho} - \rho \end{align}
ここで \(\alpha^{*}(T)\) はモルヘルツエネルギーの中のモル体積(あるいは密度)に依存しない部分で、 モル内部エネルギー、モルエントロピーなどと合致するように取っています。 このことは次の関係式から確認できます:
\begin{align} \alpha &= u - Ts \\ &= u^{*}(T) - \rho - T \left[ s^{*}(T) - \ln \frac{\rho}{1 - \rho} \right] \\ &= [u^{*}(T) - T s^{*}(T)] + T \ln \frac{\rho}{1 - \rho} - \rho \end{align}
また過剰モルヘルムホルツエネルギーは、次のように表されます:
\begin{equation} \alpha_{\rm{ex}} = - T \ln (1 - \rho) - \rho \end{equation}
|
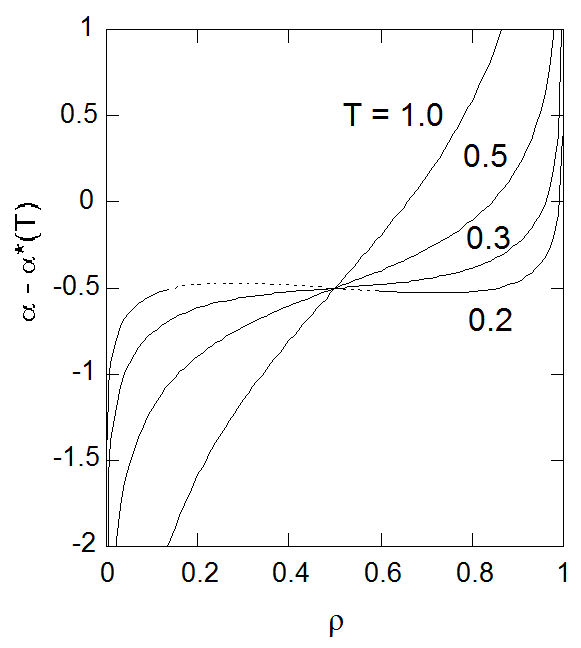
図5-2. モルヘルムホルツエネルギーの密度依存性。 図中 \(T = 0.2\) の点線部分は物質不安定性の起きる領域。 |
図5-2 にはモルヘルムホルツエネルギーの等温線を示しました。 配置のエントロピーが \(\rho = 0.5\) で0になることを反映して、 \(\rho = 0.5\) で配置のモルヘルムホルツエネルギーは温度依存性を失います。
さてもともとの状態方程式に立ち返ってみると、 \(P(T, V, N)\) の形になっているわけですから、 熱力学変数の組を \((T, V, N)\) になるように内部エネルギー \(U\) にルジャンドル変換をほどこしたヘルムホルツエネルギー \(A\) から出発すれば、 簡単な微分操作でここまで見てきた種々の熱力学量の導出が可能です (温度微分をとればエントロピー、物質量微分で化学ポテンシャル、体積微分でもとに帰って状態方程式)。 こうしたアプローチは統計力学でいえば、カノニカル状態和(分配関数)を得て、 そこから種々の熱力学量を導くという手法と同断で、見通しがよく美しいと思う方が多いかもしれません。 けれどもそれでファンデルワールス状態方程式が理解できたことになるのでしょうか? ここではそういったアプローチは取らず、 ファンデルワールス状態方程式から出発して、 一つ一つの熱力学量に寄り添い、 そこから見えるファンデルワールス状態方程式の風景を紹介しようと思います。
熱力学ポテンシャル(グランドポテンシャル) \(\Omega = -PV\) は \((T, v)\) で表現するとまさに状態方程式そのもので、 極めて簡単な構造を持ちます。 しかし熱力学ポテンシャルは、熱力学変数として \((T, V, \mu)\) を取って見た時に、 本来の意味を持つ量であることを忘れてはならないでしょう( \(\Omega = U - TS - \mu N\))。 ですからヘルムホルツエネルギーなどとは違って、 熱力学ポテンシャルはモル熱力学ポテンシャル \(\Omega/N\) といった形ではなく、 熱力学ポテンシャル密度( \(\Omega/V = -P\) )の形で議論するのが便利です。 熱力学ポテンシャル密度を、 化学ポテンシャル \(\mu\) の関数としてあからさまな形で記述するのは厄介で、 密度を用いてパラメーター表示すると、図5-3に示すような \(\mu\) 依存性が得られます。
|
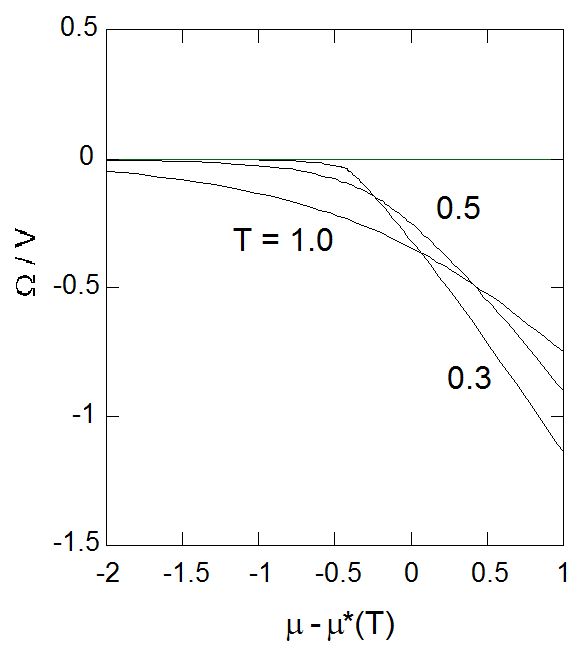
図5-3. 熱力学ポテンシャル密度( \(\Omega/V = -P\) )の化学ポテンシャル \(\mu\) 依存性。 等温線の勾配が密度 \(-\rho\) に相当する。 |
高密度では熱力学ポテンシャル密度( \(\Omega/V = -P\) )は化学ポテンシャルにほぼ比例するようになります (図の勾配が密度に対応することに注意)。 先に見たように、密度を変えた時 \(\rho = 0.2178 \ldots\) で \(\mu - \mu^{*}(T)\) は温度依存性を持たなくなって \(-0.4356 \ldots\) になるわけですが、 このことは図5-3で \(\mu - \mu^{*}(T) = -0.4356 \ldots\) で熱力学ポテンシャル密度 \(\Omega/V\) の勾配が温度を変えても変化しないことに対応しています。
臨界温度以下では、熱力学ポテンシャルの等温線に尖点(カスプ)が現れます。 等温線上の尖点は機械的不安定性(物質不安定性)の起きる点、スピノーダルに対応します。 またスピノーダル曲線にも尖点があり、これは \(TP\) 面でのスピノーダル曲線同様、臨界点に対応します。 また折れ曲がった曲線が交わる点は、次章以下で触れますが、2つの密度で圧力・化学ポテンシャルが等しくなる点、 つまり気液2相の共存点を示します。 そして共存点で交わる2つの曲線のそれぞれの勾配は、 共存点での気液の飽和密度に相当するわけです。 同様の図は縦軸にモルギブズエネルギー(つまり化学ポテンシャル)、 横軸に圧力をとる形で物理化学の教科書に紹介されますが、 ここで紹介したような熱力学ポテンシャルの立場からの理解の方が、 多成分系への拡張等を考えるとより自然なものだと思います。
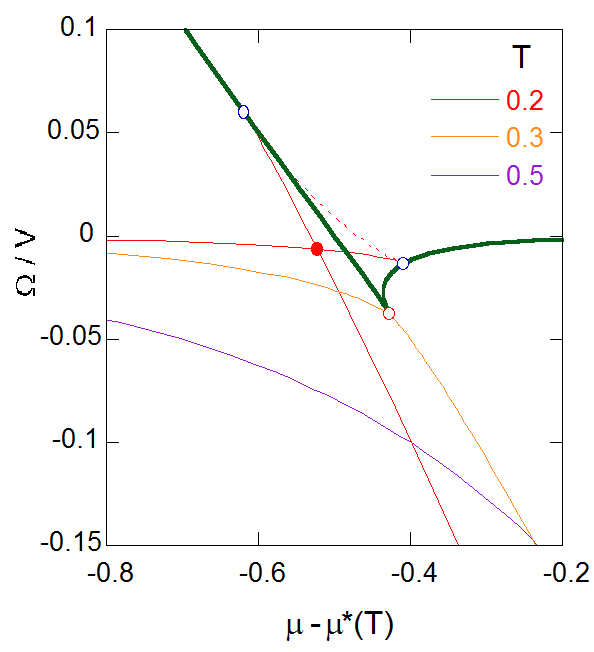
|
図5-4. 臨界温度を挟んだ、熱力学ポテンシャル密度( \(\Omega/V = -P\) )の等温線の挙動。 臨界温度( \(T_{\rm {c}} = 8/27 = 0.296\ldots\) )以下では、 等温線がスピノーダル曲線(図中緑色の線。赤丸は臨界点)で折れ曲がる。 図中 \(T = 0.2\) の等温線の点線部分は不安定領域、 青丸はスピノーダル、 塗りつぶした赤丸は、気液2相共存点に対応する。 |
今回のお話ではこれ以上触れませんが、 \(\mu P\) 面の等温線上で密度 \(\rho\) を変化させて点 \((\mu(\rho), P(\rho))\) が移動していく時、 不安定性が生じる点では \(\rmd P/\rmd \rho = \rmd \mu/\rmd \rho = 0\) が同時に成立し、 曲線の法線方向が逆転する、つまり尖点が生じることになります。 この等温線上の尖点に対応することが、そもそもの「スピノーダル曲線」の名前の由来のようです (カスプをスピノードspinode (spine(棘) + node(結び目。節))とも呼ぶようです)。 また不安定性を生じる点を結んだスピノーダル曲線にも、 \(TP\) 面上でのスピノーダル曲線の議論と同様に尖点が現れ、 これは臨界点に相当します。