相が安定に存在するのにはいくつかの条件が必要です。 すでに触れたところですが、等温圧縮率が負になると機械的な不安定性を示すので、 等温圧縮率は正でないといけません。
\begin{align} \rho \kappa_{T} &= \pdifA{\rho}{P}{T} \\ &= \frac{(1 - \rho)^2}{T - 2\rho (1 - \rho)^2} = \frac{\rho (1 - \rho)}{P - \rho^{2} (1 - 2 \rho)} \end{align}
物質不安定性に関わる次の要件
\begin{equation} \pdifA{\rho}{\mu}{T} \gt 0 \end{equation}
は1成分系では機械的安定性と同等の要件となります。 気液の臨界点というのは、こうした不安定性が起きなくなる（あるいは起きるようになる）温度・圧力条件といえ、 先にスピノーダル曲線の所で述べたところです。
\begin{align} \pdifA{P}{\rho}{T} &= 0 \\ \pdifAn{2}{P}{\rho}{T} &= 0 \end{align}
この関係が成り立つと、同様の関係式が化学ポテンシャル
\begin{align} \pdifA{\mu}{\rho}{T} &= \pdifA{\mu}{P}{T} \pdifA{P}{\rho}{T} = v \pdifA{P}{\rho}{T} = 0 \\ \pdifAn{2}{\mu}{\rho}{T} &= -\frac{1}{\rho^2} \pdifA{P}{\rho}{T} + v \pdifAn{2}{P}{\rho}{T} = 0 \end{align}
あるいは温度
\begin{align} \pdifA{T}{\rho}{P} &= -\pdifA{T}{P}{\rho} \pdifA{P}{\rho}{T} = -f(\rho) \pdifA{P}{\rho}{T} = 0 \\ \pdifAn{2}{T}{\rho}{P} &= -f'(\rho) \pdifA{P}{\rho}{T} - f(\rho) \pdifAn{2}{P}{\rho}{T} = 0 \end{align}
についても成立します。
ここからくどいようですが、臨界温度、臨界圧力、臨界密度の表式として次式が得られます：
\begin{align} T_{\rm{c}} &= \frac{8}{27} ~&\left[ = \frac{8}{27} \frac{a}{Rb} \right] \\ P_{\rm{c}} &= \frac{1}{27} ~&\left[ = \frac{1}{27} \frac{a}{b^2} \right] \\ \rho_{\rm{c}} &= 1/3 ~&\left[ = 1/(3 b) \right] \end{align}
ここで考えた不安定さは、均一な相の中で何らかの微視的な不均一さが生じた時、 その微視的なつり合いの破れが次々拡大するというものでした。 これが気液２相の分離につながるわけですが、 最終どのような圧力・組成の相が実現するかを考えてみます。 話を具体的にするため、温度は \(T = 0.25\) で一定に保たれているとし、 最初は均一な相で \(\rho = 0.4\) であったとします。
この時、機械的不安定性（物質不安定性）から低密度・高密度の２相に分離していくわけですが、 低密度相（蒸気相）は \(\rho = 0.19\) 、高密度相（液相）は \(\rho = 0.50\) になれば機械的不安定性（物質不安定性）は解消します。 しかしこれで安定になるわけではありません。 それぞれの相内の不安定性は解消しても、今度は生まれた２相の間の圧力・化学ポテンシャルのつり合いが取れていません。 蒸気相 \(\rho = 0.19\) で \((P, \mu - \mu^{*}(T))\) は \((0.023、-0.434)\) 、 液相 \(\rho = 0.50\) では \((P, \mu - \mu^{*}(T))\)は \((0、-0.5)\) です。 したがって蒸気相の膨張（あるいは物質の流出）、液相の収縮（あるいは物質の流入）が起き、 圧力・化学ポテンシャルの等しくなったところで変化は落ち着くという経緯をたどることになります。 これが気液２相の平衡状態ということになります （この時の圧力は \(P = 0.0181\) 、化学ポテンシャルは \(\mu - \mu^{*}(T) = -0.469\)）。
|
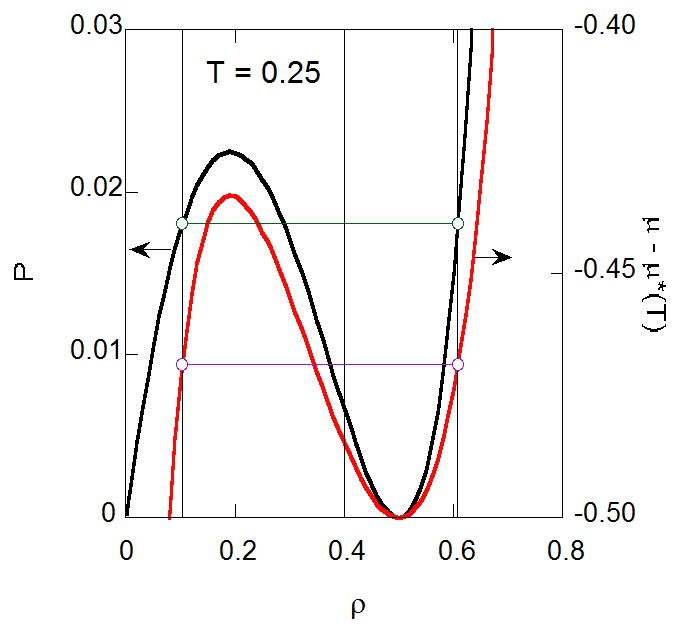
図6-1. 機械的不安定性（物質不安定性）にある流体の等温的な相分離にともなう、
圧力（黒い曲線）・化学ポテンシャル（赤い曲線）の変化の挙動。
温度 \(T = 0.25\) で、初期密度 \(\rho = 0.4\) の状態におかれた流体は相分離し、 最終的に密度 \(\rho = 0.103\) の蒸気相と \(\rho = 0.608\) の液相を形成する。 ２相共存平衡時の圧力は \(P = 0.0181\) （図中緑の線）、 化学ポテンシャルは \(\mu - \mu^{*}(T) = -0.469\) （図中紫の線）。 |
気液２相の共存条件は、温度が等しいという条件の下、 圧力・化学ポテンシャルのつり合いを与える次の連立方程式を解けば得られます：
\begin{align} P(T, x) &= P(T, y) \\ \mu(T, x) &= \mu(T, y) \\ \end{align}
ここで\(x\)は液相の、\(y\)は蒸気相（気相）の密度（つまり\(x \gt y\)）を表すものとします。 後の議論とも関係する部分があるので、この節では、 圧力が等しくなるだけでは不十分で、化学ポテンシャルのつり合いも必要になる事情を、 近似計算を取り入れて少し詳細に見ておきます。
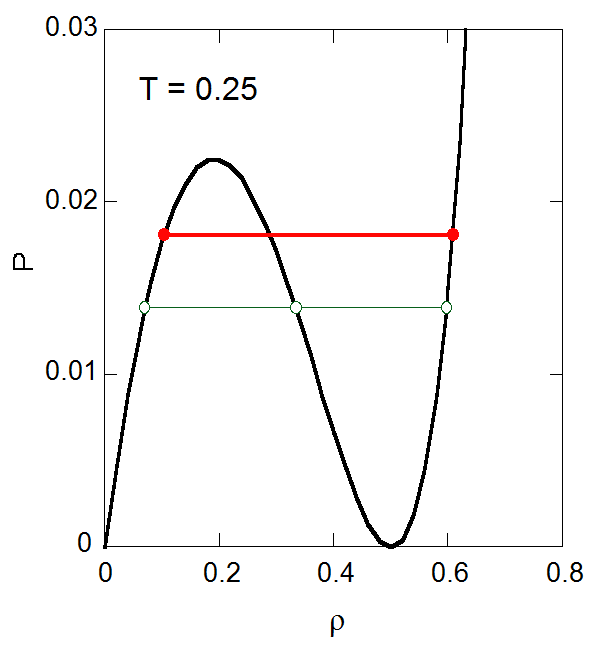
図 6-2 には \(P\rho\) 面における \(T = 0.25\) の場合の等温線の挙動を示しました。 ファンデルワールス状態方程式は、密度についての3次式の形で書くと次のようになります：
\begin{equation} \rho^3 - \rho^2 + (P + T)\rho - P = 0 \end{equation}
気液の相分離が起きる場合には、温度 \(T\) を与えたとすると平衡圧力で \(\rho\) には３個の実根があり、 これを \(\rho_{1} \lt \rho_{2} \lt \rho_{3}\) とします。 ここで気液の平衡密度の平均 \((\rho_{1} + \rho_{3})/2\) が臨界密度 \(1/3\) に等しいとしてみましょう （直径線の法則で温度依存性を無視したことに相当）。 この近似は臨界点の近くではよい近似になっていると考えられます。 さて \((\rho_{1} + \rho_{3})/2 = 1/3\) と仮定すると、 根と係数の関係から\(\rho_{1} + \rho_{2} + \rho_{3} = 1\) が成り立っているので、 この中間の根 \(\rho_{2}\) （不安定状態に相当）は臨界密度1/3に等しくなります。 また \(\rho_{1}\) と \(\rho_{3}\) は次の２次方程式の根です：
\begin{equation} \rho^2 - (2/3)\rho - 3P = 0 \end{equation}
ですから、\(\rho_{1}\) と \(\rho_{3}\) は次の式で与えられることになります（復号が \(-\) は \(\rho_1\) 、+ は \(\rho_3\) ）：
\begin{equation} \rho ＝ \frac{1}{3} \pm \sqrt{\frac{1}{9} - 3P} = 0 \end{equation}
臨界圧力 \(P_{\rm{c}} = 1/27\) からの差 \(\pi = P - P_{\rm{c}}\) を用いるとさらに簡単に表記できます。
\begin{equation} \rho ＝ \frac{1}{3} \pm \sqrt{- 3\pi} \end{equation}
同様に温度を用いても表すことができ、 臨界温度 \(T_{\rm{c}} = 8/27\) からの差 \(\tau = T - T_{\rm{c}}\) を用いると簡単に表記できます。
\begin{equation} \rho ＝ \frac{1}{3} \pm \sqrt{- \frac{2}{3}\tau} \end{equation}
|
|
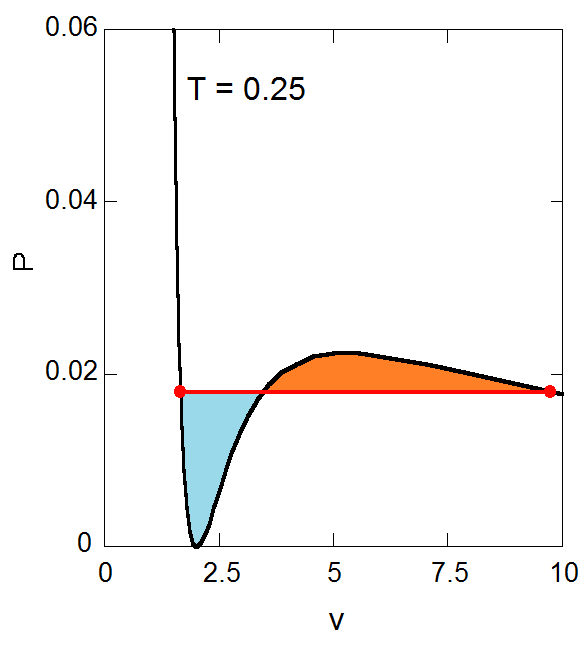
| 図6-2. 気液の密度の平均値が臨界密度に等しいと仮定した場合の平衡密度の評価。 | 図6-3. マクスウェルの等面積則。 図の青色の部分と橙色の部分の面積が等しくなるように、平衡圧力の線を引く。 |
こうした近似的な手法で求めたのが図6-2 の緑色の線です。 一方図6-2 に赤線で示してあるのは、圧力と化学ポテンシャルのつり合いから決まる平衡圧力です。 近似的な手法では \(T = 0.25\) では圧力が \(0.0139\) で、 化学ポテンシャルのつり合いも考えて得られる平衡圧力 \(0.0181\) に対し、まったく見当外れというわけではありませんが、 かなり過小評価してしまいます。 精確なところを知るためには、まっとうに非線形の方程式と取り組む必要があります。
なおこの平衡圧力を求める手法として古来有名なマクスウェルの等面積則 Maxwell equal area rule （あるいはマクスウェルの作図 Maxwell construction）と呼ばれるものは、 図6-3 のように横軸に密度の代わりにモル体積を取り、 等温線から平衡圧の直線で切り取られる２つの部分の面積（図の青と橙色の部分）が等しくなるように平衡圧を決めるというものです。 これは化学ポテンシャルの表式を導いた５章の式(3)を見てもらうと、 化学ポテンシャルが等しくなるように決めるのと同じことになっていて、 先の連立方程式を解くのと同じであることがわかります。
歴史的にはアンドリュースによる二酸化炭素の臨界点の実験(1869年)に触発されてマクスウェルが等面積則を創出し(1871年。"Theory of Heat")、 ファンデルワールスが分子論的な考察で導出した状態方程式にそれを適用する(1873年)という足取りをたどります。
気液２相の共存条件は、温度が等しいという条件の下、 圧力・化学ポテンシャルのつり合いを与える次の連立方程式を解けば得られます：
\begin{align} \Delta P(x, y) &= P(x) - P(y) \\ \Delta \mu(x, y) &= \mu(x) - \mu(y) \end{align}
ここで\(x\)は液相の、\(y\)は蒸気相（気相）の密度（つまり\(x \gt y\)）です。 こうした式を書き下すのは簡単ですが、実際に解を求めるのは結構厄介です。 与えられた温度における気液の平衡密度（飽和密度）を求めるには、 非線形の連立方程式を解かないといけないのですが、 初等的な解法は無理で、数値計算に頼らざるを得ません。 数値計算にはニュートン法を用いるのが便利です。
ある温度\(T\)で液相・蒸気相の密度として\((x, y)\)を与えた時、圧力に\(\Delta P(x, y)\)、 化学ポテンシャルに\(\Delta \mu(x, y)\)の違いがあったとします（引数の\(T\)は省略します）
\begin{align} \Delta P(x, y) &= P(x) - P(y) \\ \Delta \mu(x, y) &= \mu(x) - \mu(y) \end{align}
ここで先に見た次の関係に注目します
\begin{equation} \rho \left( \frac{\partial \mu}{\partial \rho} \right)_{T} = \left( \frac{\partial P}{\partial \rho} \right)_{T} \end{equation}
するとある適当な密度の組み合わせ\((x, y)\)の微小量の変化\((\delta x, \delta y)\)に対し次の関係を得ます：
\begin{equation} \begin{pmatrix} \Delta P(x, y) \\ \Delta \mu(x, y) \end{pmatrix} = \begin{pmatrix} x & -y \\ 1 & -1 \end{pmatrix} \begin{pmatrix} \mu' (x) \delta x \\ \mu' (y) \delta y \end{pmatrix} \end{equation}
したがって適当な初期値から始めて、次のような逐次近似を繰り返せば、 設定した温度における液相・蒸気相の密度を得ることができるわけです：
前節で紹介した数値計算の手法は直接的で、他のタイプの状態方程式にも容易に拡張できて適用範囲が広く、 今日的には推奨されるものであると思います。 けれども古くからおこなわれてきたパラメーター表示で平衡密度を表示する手法も記憶されていてよいでしょう。 以下で紹介するような計算を行って、平衡密度に関してパラメーター化した方程式の形で解を与えたのは、 今では量子力学で有名なプランクでした。
プランクの1881年の論文（M. Planck, Ann. Physik 249 [13], 535 (1881)）で扱われているのは
\[
P = \frac{RT}{v - \alpha} - \frac{c}{T (v + \beta)^2}
\]
という形の状態方程式です（当時クラウジウスが二酸化炭素の \(pvT\) をよりよく再現する式として提唱していた模様）。
プランクの取り扱いは、ファンデルワールス状態方程式にも適用可能ですが、そのためには式を次のように変形し
\[
PT = \frac{RT^2}{v - \alpha} - \frac{c}{(v + \beta)^2}
\]
ここで \(v' = v + \beta\) として、 \(PT\) を圧力 \(P\) 、 \(T^{2}\) を温度 \(T\) と読み替えることになります。
なおプランクが刊行した1880年の論文（未見。学位論文？）の中には、
より詳細な叙述がある由で、もしかするとそこでファンデルワールス状態方程式も扱われていたかもしれません。
まず圧力のつり合いの式をあからさまに書くと次のようになります：
\begin{equation} P(x) = \frac{xT}{1 - x} - x^2 = \frac{yT}{1 - y} - y^2 = P(y) \end{equation}
ここから次の関係が得られ
\begin{equation} \frac{x - y}{(1 - x)(1 - y)} T = (x - y)(x + y) \end{equation}
ここで \(x \ne y\) なので温度 \(T\) は次式のように気液の飽和密度で表されます：
\begin{equation} T = (1 - x)(1 - y)(x + y) \label{eq:tcoex} \end{equation}
次に化学ポテンシャルのつり合いの式をあからさまに書くと
\begin{equation} \mu(x) - \mu^{*} = \frac{xT}{1 - x} + T \ln \left( \frac{x}{1 - x} \right) - 2x = \frac{yT}{1 - y} + T \ln \left( \frac{y}{1 - y} \right) - 2y = \mu(y) - \mu^{*} \end{equation}
ここから次の関係を得、
\begin{equation} T \ln \left( \frac{x (1 - y)}{y (1 - x)} \right) = \frac{x - y}{(1 - x)(1 - y)} T + 2(x - y) \end{equation}
先の温度の表現を代入して次の飽和密度 \((x, y)\) についての関係式がえられます
\begin{equation} \ln \left( \frac{x (1 - y)}{y (1 - x)} \right) = \frac{(x - y)(2 - x- y)}{(1 - x)(1 - y)(x + y)} \end{equation}
式の見通しをよくするため、次の変数 \(X, Y\) を導入します
\begin{align} X = f(x) = \frac{x}{1 - x} \\ Y = f(y) = \frac{y}{1 - y} \end{align}
\(X, Y\) を使って式を書きなおすと次のようになります
\begin{equation} \ln \frac{X}{Y} = \frac{(X - Y)(2 + X + Y)}{2XY + X + Y} \end{equation}
ここでプランクにならって次のように、パラメータ \(r\) と \(\theta\) を用いて \(X\) と \(Y\) を表します （ \(0 \lt \theta \lt \pi/2\) ）
\begin{align} X = r \cos^{2} \frac{\theta}{2} \\ Y = r \sin^{2} \frac{\theta}{2} \end{align}
これを式に代入すると次の関係を得ます
\begin{equation} \ln (\cot \frac{\theta}{2}) = \frac{(2 + r) \cos \theta}{2 + r \sin^{2} \theta} \end{equation}
これを \(r\) について解けば
\begin{equation} \frac{r}{2} = -\frac{\cos \theta + \ln (\tan \frac{\theta}{2})}{\cos \theta + \sin^{2} \theta \ln (\tan \frac{\theta}{2})} \end{equation}
したがって、 \(\theta\) に何らかの数値を入れてやればここから \(r\) が求まり、 \(r\) と \(\theta\) が定まれば \(X\) と \(Y\) が定まり、気液の飽和密度 \(x\) と \(y\) が決まる。 そこから式 \eqref{eq:tcoex} の関係から温度 \(T\) 、さらに状態方程式から圧力 \(P\)は自ずと決まるというわけです。 これで解が求まったことになるわけですが「ある温度での飽和密度を知りたい」という要望に直ちに応えられません。 また式が複雑でいささか見通しが悪く、少なくともぼくの手元の教科書類では見かけません （M. PlanckのTreatise on Thermodynamics（第３版の翻訳1926）にもありません）。 ぼくなどには何か懐かしい香りがあるので、忘れられてしまうのは惜しいですが・・・