|
|
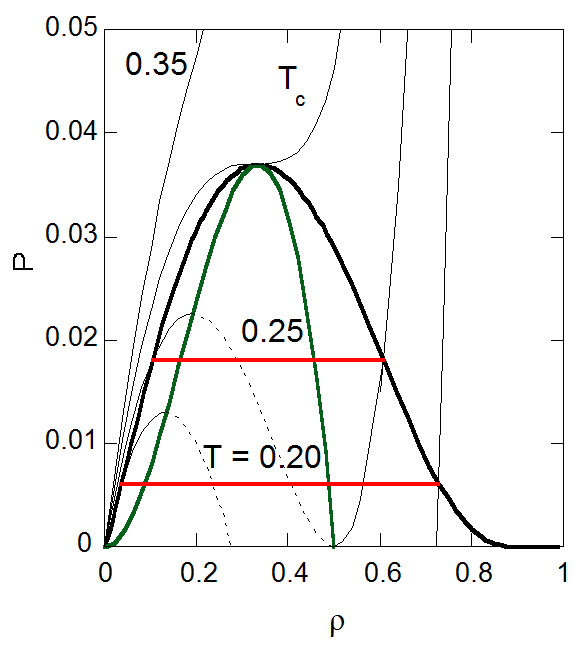
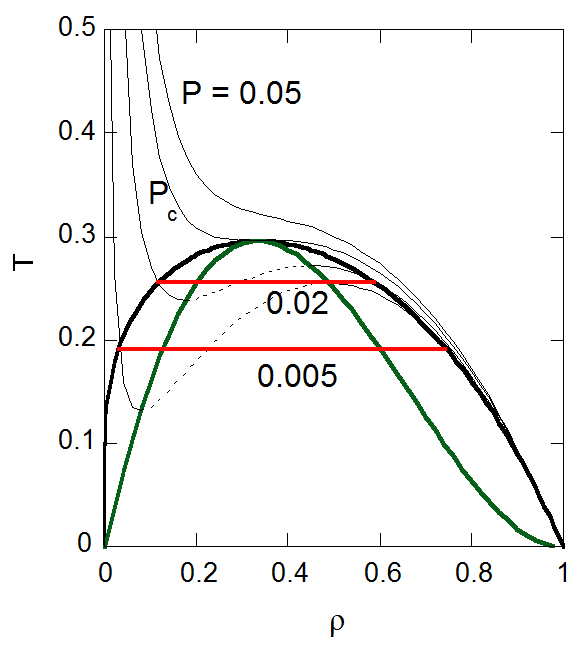
| 図7-1. ファンデルワールス状態方程式から得られる \(\rho P\) 面における飽和密度曲線。 緑の線はスピノーダル曲線、等温線の破線部分は不安定領域。 | 図7-2. ファンデルワールス状態方程式から得られる \(\rho T\) 面における飽和密度曲線。 緑の線はスピノーダル曲線、等圧線の破線部分は不安定領域。 |
ファンデルワールス状態方程式に基づく気液平衡の計算はすでに多数行われてきたはずだと思うのですが、手近な本に見当たらないので、 表7-1と図7-1、7-2に実際に計算した結果を示します。
| \(T\) | \(P\) | \(y\) | \(x\) |
| 0.29630 | 0.03704 | 0.333 | 0.333 |
| 0.296 | 0.03689 | 0.312 | 0.354 |
| 0.294 | 0.03590 | 0.276 | 0.393 |
| 0.292 | 0.03493 | 0.255 | 0.415 |
| 0.29 | 0.03397 | 0.240 | 0.433 |
| 0.28 | 0.02942 | 0.187 | 0.495 |
| 0.26 | 0.02149 | 0.125 | 0.576 |
| 0.24 | 0.01503 | 0.085 | 0.636 |
| 0.22 | 0.00996 | 0.056 | 0.686 |
| 0.20 | 0.00615 | 0.036 | 0.729 |
| 0.18 | 0.00346 | 0.021 | 0.767 |
| 0.16 | 0.00170 | 0.011 | 0.801 |
| 0.14 | 0.00069 | 0.005 | 0.832 |
| 0.12 | 0.00021 | 0.002 | 0.861 |
| 0.10 | 0.00004 | 0.000 | 0.887 |

|

|
| 図7-1. ファンデルワールス状態方程式から得られる \(\rho P\) 面における飽和密度曲線。 緑の線はスピノーダル曲線、等温線の破線部分は不安定領域。 | 図7-2. ファンデルワールス状態方程式から得られる \(\rho T\) 面における飽和密度曲線。 緑の線はスピノーダル曲線、等圧線の破線部分は不安定領域。 |
現実の物質では固相が出現したり、もっと複雑な挙動を示しますが、 ファンデルワールス状態方程式にのみよる限り2相が現れるだけです。 飽和密度線は、縦軸に圧力をとった場合と温度を取った場合で、 臨界点近傍については坊主頭の似通った形ですが、 臨界点から外れに従ってそれぞれの個性が現れます。
密度-圧力で取った場合、低圧・低密度の蒸気相に注目するとほぼ直線的に飽和密度線が立ち上がっていきます。 後でも触れますが、これは低圧側で蒸気密度 \(y\) が \(-P \ln P\) で評価されることに対応しています。 また低圧・高密度の液相で密度の増加とともに平衡圧力が急激に減少していくのは、 液相密度が温度の低下とともに直線的に増加する一方で、 蒸気圧が指数関数的に減少することに対応しています。
密度-温度で取った場合は、密度-圧力で取った場合に比べて全体にずんぐりした形状になります。 低温・低密度の蒸気相では、蒸気密度の増大に従って急激に平衡温度は増大していきます ( \(T = 0.1\) でも \(y = 0.0004\) でほぼ縦軸に張り付いています)。 これは蒸気圧が温度の逆数に対し指数関数的に増加することに対応しています。 また低温・高密度側では、平衡温度が下がるにしたがってほぼ温度に比例して密度が1になりますが、 これは後述するバチンスキーの法則といわれるものに対応しています。
このようなずんぐり型の飽和密度の温度依存性については、 直径線の法則(カイユテ-マチアスCailletet - Mathiasの法則)が成り立つことが知られています。 これは気液の飽和密度の平均が、温度に比例する直線になるというものです。
\begin{equation} \frac{x + y}{2} = \rho_{\rm{c}} + k (T_{\rm{c}} - T) \label{eq:diameter} \end{equation}
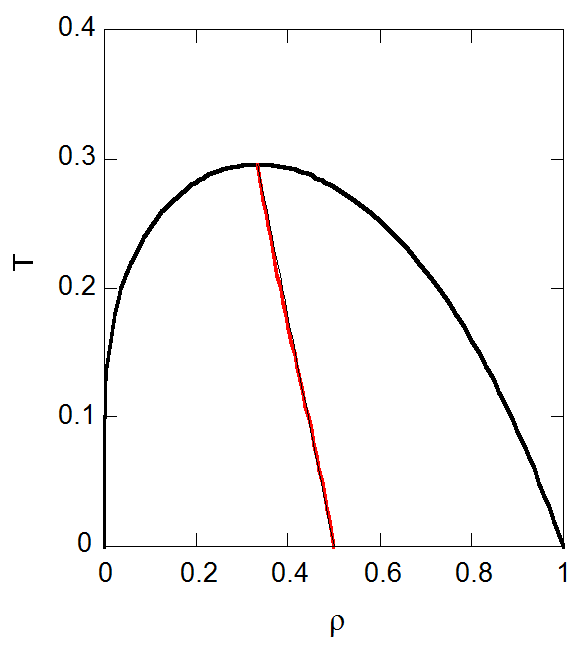
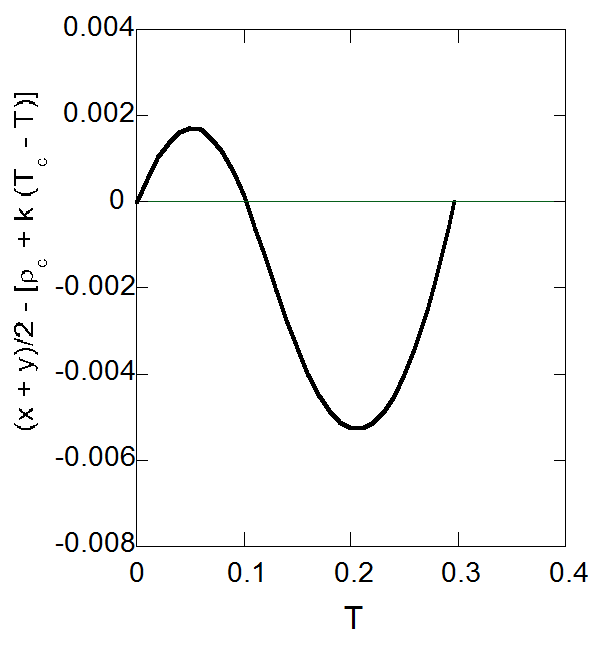
もしこの関係が臨界点から \(T = 0\) にいたるまで正確に成立するなら、 \(k = 9/16\) になるはずです。 ファンデルワールス状態方程式から得られる相図では、厳密に成り立つわけではありませんが、 図7-3に示すように、低温に至るまでよい近似で成り立っています。 図7-3b には式からの偏差を示しましたが、低温側で正に、高温側で負に若干振れますが、偏差は最大で1.4%程度です。 同様のことを飽和密度の圧力依存性について試みても、低圧側に行くにつれて偏差が大きくなり成功しません。
|
|
| 図7-3a. 気液の飽和密度の平均値の温度依存性(直径線の法則)。 | 図7-3b. 直径線の法則からの偏倚。 |
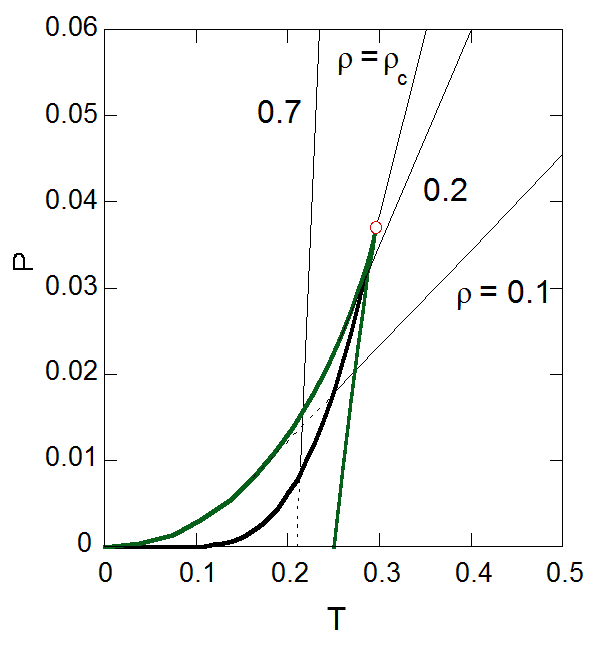
ここでTP面の挙動、蒸気圧曲線に注目してみましょう。 図7-4 には蒸気圧曲線とスピノーダル曲線を示しました。 先に見たようにスピノーダル曲線は等密度線の包絡線に相当し、逆にスピノーダル曲線の接線は等密度線になります。蒸気圧曲線は臨界点でスピノーダル曲線のカスプと交わります。
|
図7-4. 蒸気圧曲線とスピノーダル曲線。 図中、等密度線の破線部分は過冷却・過熱領域にあることを示す。 |
等密度線に沿って流体の温度を下げていくことを考えると、 蒸気圧曲線を通り過ぎても、過熱あるいは過冷却状態の形でスピノーダル曲線まで1相で比較的安定に存在することができます。 では蒸気圧曲線と交わるところで、もっとも安定な状態である気液2相分離した状態になったとして、 さらに温度を下げていったらどうなるでしょう? もし密度が臨界密度以下であれば蒸気圧曲線に達したところで液体の生成(凝縮)が起き、 臨界密度以上であれば蒸気の発生(沸騰)が起きるはずです。 ある一定体積の容器中で、密度 \(\rho\) の流体を冷却し、こうした2相分離が起きるとしましょう。 この時、全体の中の液体の占める体積の割合 \(V_{L}/V\) は、 その温度における液体・蒸気の平衡密度 \(x\) と \(y\) を用いて次式で表されます:
\begin{equation} \frac{V_{L}}{V} = \frac{\rho - y}{x - y} \end{equation}
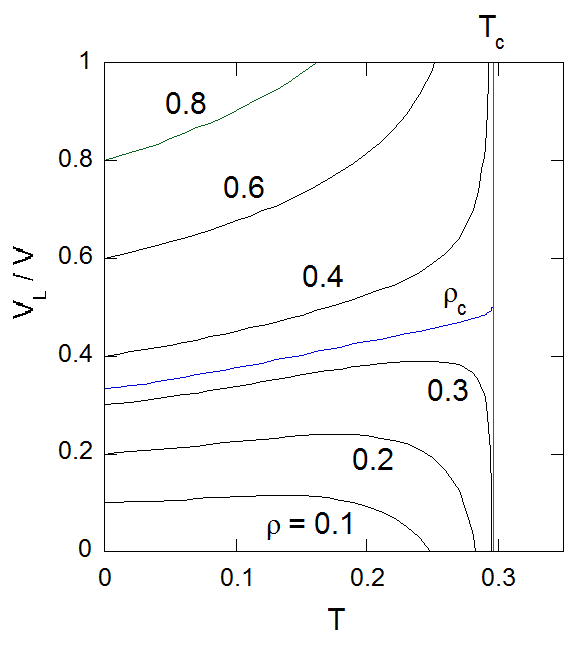
図7-5 には種々の密度の流体を臨界温度以上から密度 \(\rho\) 一定で冷却していった時、 生じる液相の体積比 \(V_{L}/V\) の温度変化示しました。 この図で等密度線が \(V_{L}/V= 1\) あるいは \(V_{L}/V= 0\) に達する温度はそれぞれ沸点・露点に対応することになります。 温度を下げていくと低密度では凝縮した液相が増えていき、 ある極大に達した後、液相は収縮していきます。 一方高密度では温度を下げるにつれ、気相(泡)が生じた後、 液相の収縮が一貫して続きます。 なおファンデルワールス状態方程式による限り、 温度を下げていった時、生じた液相が再び消失、 あるいは生じた気相が再び消失したりすることは起きません(等密度線は蒸気圧曲線と2カ所で交わることがない)。
|
図7-5. 2相共存域での、温度変化にともなう液相の体積比の変化。 |
通常われわれが常圧下で液体と認識するのは蒸気圧が1気圧以下、 せいぜい0.1気圧程度の流体です。 たいていの液体の臨界圧力は数十~百気圧ぐらいですから、 今回の圧力のスケールでいうと \(0.0001\) 以下程度で温度は \(0.1\) 以下というところです。 こうした状態では液体側の密度 \(x\) を扱う上で、平衡圧力(蒸気圧)を \(0\) とおく近似が有効になります:
\begin{equation} P = \frac{xT}{1 - x} - x^2 \approx 0 \label{eq:vdw0} \end{equation}
したがってここから
\begin{equation} x - x^2 \approx T \end{equation}
となり、液相の密度はほぼ温度に比例することになります:
\begin{equation} x \approx \frac{1 + \sqrt{1 - 4T}}{2} \approx 1 - T \label{eq:batschinski} \end{equation}
これはバチンスキーBatschinski の法則といわれる関係式に相当します。 図7-2で低温・液相側の飽和密度線が、平衡温度に比例して減少していくのはこのことに対応しています。 また直径線の法則(式 \eqref{eq:diameter})からは、 \(x \approx 1 - (9/8) T\) になるはずですが、 温度依存性は若干小さくなります。 これは図7-3b で、直径線の法則が低温側で気液の平均密度を少し小さく評価していることに対応しています。 なお式 \eqref{eq:batschinski} で、もう一つの根 \((1 - \sqrt{1 - 4T})/2\) は不安定な解に相当し実現しません (式 \eqref{eq:vdw0} の根として \(\rho = 0\) と \((1 \pm \sqrt{1 - 4T})/2\) がえられ、 \(0 \lt (1 - \sqrt{1 - 4T})/2 \lt (1 + \sqrt{1 - 4T})/2\) であることに注意してください)。
蒸気相の密度 \(y\) を求めるには、化学ポテンシャルが次のように書けることに注意します( \(O(T^{2})\) は無視):
\begin{align} \mu - \mu^{*}(T) &=T \ln \frac{x}{1 - x} + \frac{xT}{1 - x} - 2x \\ &\approx T \ln \frac{x}{1 - x} + x^{2} - 2x \\ &\approx T \ln \frac{1 - T}{T} - 1 \end{align}
蒸気相の密度 \(y\) は、 \(y \ll 1\) に注意して
\begin{align} \mu - \mu^{*}(T) &= T \ln \frac{y}{1 - y} + \frac{yT}{1 - y} - 2y \\ &\approx T \ln y \end{align}
であることから、次式のように表されます:
\begin{equation} y \approx \frac{1 - T}{T} \exp \left( -\frac{1}{T} \right) \end{equation}
さらに蒸気圧は次式で与えられます:
\begin{align} P &\approx yT \\ &\approx (1 - T) \exp \left( -\frac{1}{T} \right) \label{eq:vaporpressure} \end{align}
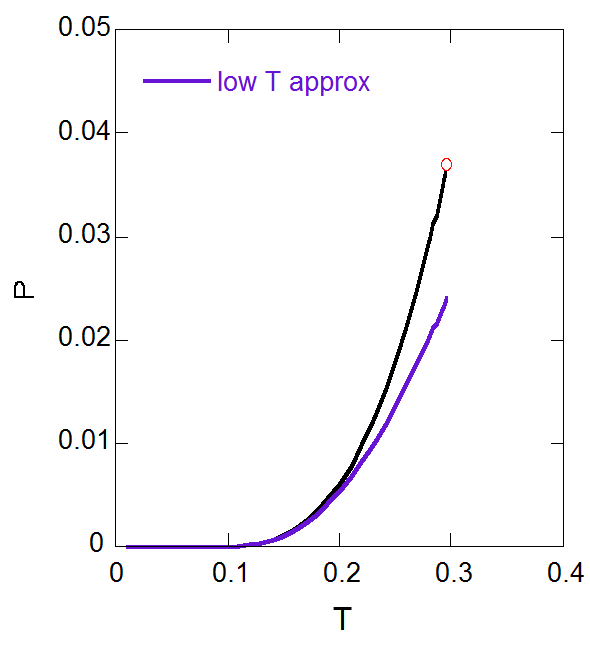
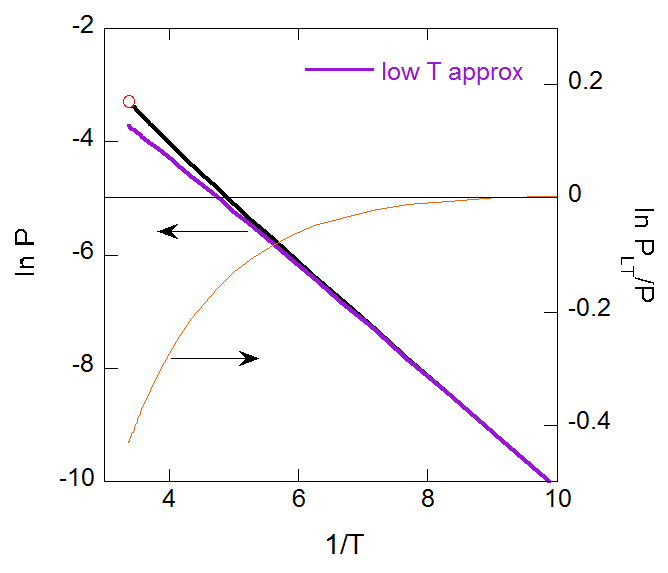
正確な蒸気圧曲線と比較してみると、温度が \(T = 0.15\) 程度以上では蒸気圧を過小評価しますが、 それ以下では近似が非常に良く成り立っていることがわかります。
|
|
| 図7-6a. 蒸気圧に対する近似式と厳密に計算された蒸気圧との比較。 | 図7-6b. 対数スケールで見た蒸気圧の近似式の偏倚。 |
なお十分 \(T\) が小さければ \(1/T \approx -\ln P\) であることに注意して、 蒸気圧 \(P\) と蒸気密度 \(y\) の関係として次式を得ることができます:
\begin{equation} y \approx - P \ln P \end{equation}
図6-1で見た低圧・蒸気側の飽和密度線の挙動はこのことに対応しています。
さて蒸気圧曲線については、その勾配 \(\rmd P/\rmd T\) は相変化にともなうエントロピー変化 \(\Delta s\) 、 体積変化 \(\Delta v\) との間に、次のクラペイロン-クラウジウスの式が成立します
\begin{equation} \frac{\rmd P}{\rmd T} = \frac{\Delta s}{\Delta v} \end{equation}
蒸発のエントロピー変化 \(\Delta s\) は蒸気のモルエントロピー \(s_{\rm{G}}\) と液体のモルエントロピー \(s_{\rm{L}}\) の差で、 ファンデルワールス流体の配置のモルエントロピーは密度のみで決まるので、 気液の平衡密度を用いて次式のように表されます:
\begin{equation} \Delta s = s_{\rm{G}} - s_{\rm{L}} = -\ln \frac{y (1 - x)}{x (1 - y)} \end{equation}
ここで低温・低圧域で成り立つ先の関係を用いれば、エントロピー変化について
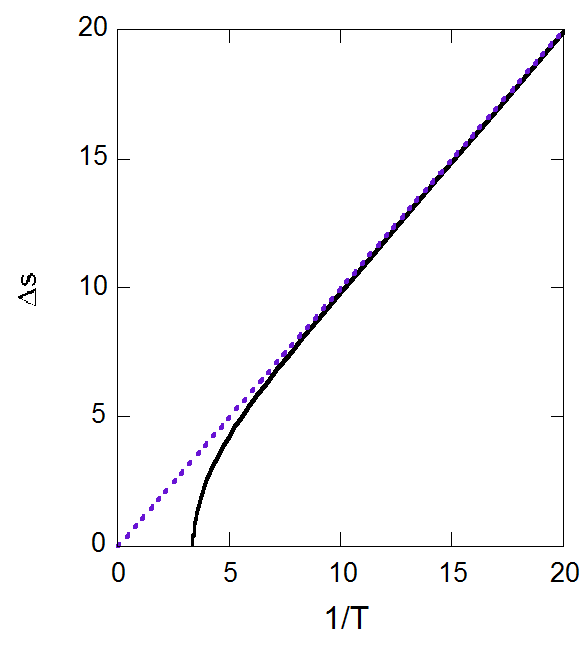
\begin{equation} \Delta s \approx -\ln \frac{yT}{1 - T} = \frac{1}{T} \end{equation}
という関係を得ます。 実際に計算したエントロピー変化の温度変化を図に示しますが、 \(T \lt 0.15\) 程度であれば、この関係は極めてよく成立しています。
|
図7-7. 蒸発のエントロピー変化 \(\Delta s\) の温度依存性。 |
なおわれわれの身近に見る液体について、 標準沸点での蒸発のエントロピーがほぼ \(10 R\) になるというトルートン Trouton の通則はよく知られていますが、 ファンデルワールス状態方程式からだけでは説明は困難です。
さてクラペイロン-クラウジウスの式に立ち返ると、 蒸発にともなう体積変化 \(\Delta v\) は、 蒸気のモル体積 \(1/y\) が液体のモル体積 \(1/x\) より圧倒的に大きいのでほぼ \(1/y\) に等しく、
\begin{align} \frac{\rmd P}{\rmd T} &= \frac{\Delta s}{\Delta v} \\ &\approx \frac{y}{T} = \frac{1 - T}{T^2} \exp(-\frac{1}{T}) \end{align}
という表現を得ます。 これは先の蒸気圧の式 \eqref{eq:vaporpressure} を温度微分して得られる式で \(O(T^{2})\) の項を落としたものになっています。
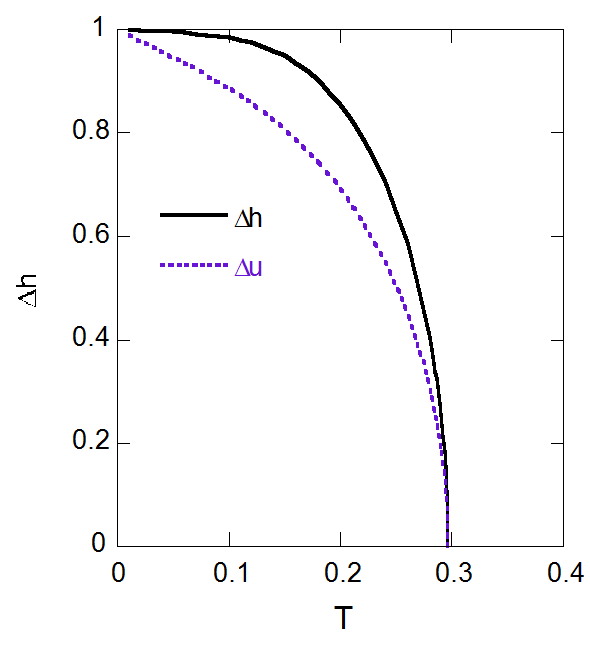
さて蒸発のエンタルピー変化 \(\Delta h\) はエントロピー変化 \(\Delta s\) に温度をかけたものに等しく、 温度によらずほぼ一定ということになります:
\begin{align} \Delta h &= T \Delta s \\ &\approx T \frac{1}{T} = 1 \end{align}
この一方、蒸発の内部エネルギー変化は蒸気と液体の密度差に等しく、温度の上昇とともに減少します:
\begin{align} \Delta u &= x - y \\ &\approx x \approx 1 - T \end{align}
実際にこれを確認してみたのが図 7-8 です。 低温では内部エネルギー変化がほぼTに比例して減少していくのに対し、 エンタルピー変化の変動は小さいものにとどまっています。 内部エネルギー変化の減少を、 蒸気になって膨張することにともなう \(PV\) 仕事が打ち消す構造といってよいでしょう。
|
図7-8. 蒸発のエンタルピー変化 \(\Delta h\) と内部エネルギー変化 \(\Delta u\) の温度依存性。 |
気液の臨界点近傍の挙動は、 今日スケーリング理論などに立脚した臨界現象の一般論の枠組みの中で議論されています。 しかしファンデルワールス状態方程式それ自体に寄り添った形での議論は、 ランダウの理論や平均場近似一般の議論に付属する形で行われ、 必ずしも十分知られていないように見えます。 ここでは初歩的な形で、ファンデルワールス流体の臨界点近傍の挙動を臨界指数などに注目する形で紹介しておきましょう。
まず臨界点における状態方程式の挙動を復習しておきましょう。臨界点では次の条件が成立します:
\begin{align} \left( \frac{\partial P}{\partial \rho} \right)_{T} &= T f'(\rho) - 2\rho = 0 \\ \left( \frac{\partial^2 P}{\partial \rho^2} \right)_{T} &= T f''(\rho) - 2 = 0 \\ \end{align}
また同様に化学ポテンシャルについて次の条件が成立します
\begin{align} \pdifA{\mu}{\rho}{T} &= \pdifA{\mu}{P}{T} \pdifA{P}{\rho}{T} = v \pdifA{P}{\rho}{T} = \frac{T}{\rho} f'(\rho) - 2 = 0 \\ \pdifAn{2}{\mu}{\rho}{T} &= -\frac{1}{\rho^2} \pdifA{P}{\rho}{T} + v \pdifAn{2}{P}{\rho}{T} = - \frac{T}{\rho^2} [f'(\rho) - \rho f''(\rho)] = 0 \label{eq:dmuddd} \end{align}
くどいですが、ここから臨界温度、臨界圧力、臨界密度の表式として次式が得られます:
\begin{align} T_{\rm{c}} &= \frac{8}{27} \\ P_{\rm{c}} &= \frac{1}{27} \\ \rho_{\rm{c}} &= 1/3 \end{align}
この臨界点の近くでの相挙動を議論する上で、 臨界点周りで圧力・化学ポテンシャルを温度・密度について級数展開することを考えます。 そのために、温度・密度について次のようなパラメーターを用意します。
\begin{align} \tau &= T - T_{\rm{c}} \\ z &= \rho - \rho_{\rm{c}} \end{align}
以下ではもっぱら、臨界温度以下の温度領域での挙動を問題にすることにします(\(\tau \lt 0\))。 そして\(z \lt 0\)は蒸気相、\(z \gt 0\)は液相を意味するわけです。
さて臨界点周りで、圧力・化学ポテンシャルを\(\tau\)と\(z\)のベキで展開するわけですが、 温度\(\tau\)については1次から取ればいいのですが、 密度\(z\)については2階微分まで0なのでちょっと注意が必要です。 実際に展開項を計算してみると次のような式を得ます
\begin{align} P(\tau, z) &= P_{\rm{c}} + P_\tau \tau + P_{\tau \rho} \tau z + \frac{1}{2!} P_{\tau \rho \rho} \tau z^2 + \frac{1}{3!} P_{\rho \rho \rho} z^3 \label{eq:pexpand} \\ &= \frac{1}{27} + \frac{1}{2} \tau + \frac{9}{4} \tau z + \frac{27}{8} \tau z^2 + \frac{3}{2} z^3 \end{align}
\begin{align} \mu(\tau, z) &= \mu_{\rm{c}} + \mu_\tau \tau + \mu_{\tau \rho} \tau z + \frac{1}{3!} \mu_{\rho \rho \rho} z^3 \\ &= \mu_{\rm{c}} + \mu_{\tau} \tau + \frac{27}{4} \tau z + \frac{9}{2} z^3 \end{align}
ここで臨界点における偏微分係数を次のように略記しています:
\begin{equation} X_\tau = \pdifA{X}{\tau}{z}, ~~X_\rho = \pdifA{X}{z}{\tau} \end{equation}
化学ポテンシャルについて \(\tau z^2\) の項が現れないのは、 式\eqref{eq:dmuddd} に見たように \(\partial^2 \mu/\partial \rho^2\) が \(T\) に比例するためです:
\begin{equation} \mu_{\tau \rho \rho} = \frac{1}{T} \mu_{\rho \rho} = 0 \end{equation}
さてここで\(\tau \lt 0\)の下で、
\begin{align} P(\tau, z_1) &= P(\tau, z_2) \\ \mu(\tau, z_1) &= \mu(\tau, z_2) \\ \end{align}
を満たすような\(z_1 \gt z_2\)を求めることを考えます。 すると\(\mu (z_1) =\mu(z_2)\)から
\begin{equation} -\frac{3}{2} \tau =z_1^2 + z_1 z_2 + z_2^2 \end{equation}
\(P (z_1) =P (z_2)\)と上の条件から、液相と蒸気相の密度については次の結果がえられます。
\begin{equation} z_1 + z_2 = 0 \end{equation}
したがって6-2節で取り上げた近似計算と同様に、\(z_1\)、\(z_1\)の表現として次式が得られます:
\begin{equation} z_1 = - z_2 = \sqrt{{\frac{3}{2} \tau}} \end{equation}
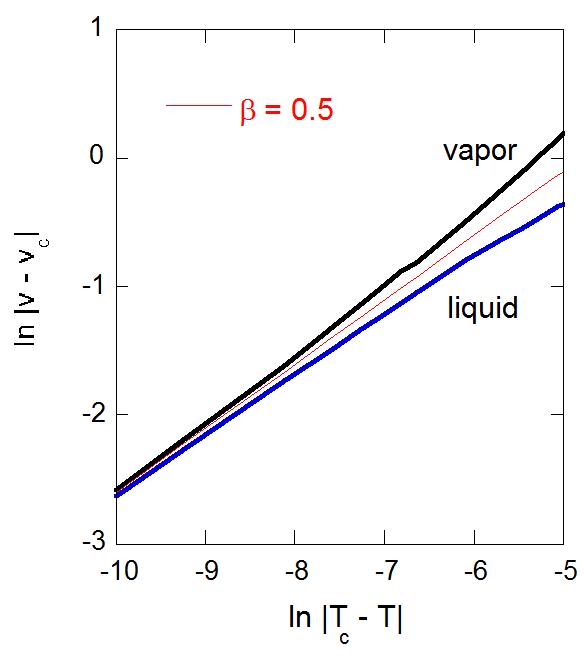
臨界点近傍で次のような関係から、 臨界指数\(\beta\) が定義されます。
\begin{align} | v_{{\rm {L}}} -v_{{\rm {c}}} | \propto |\tau|^{\beta} \\ | v_{{\rm {G}}} -v_{{\rm {c}}} | \propto |\tau|^{\beta} \\ \end{align}
ファンデルワールス流体の\(\beta\) は1/2というわけです。
|
図7-9. 臨界点における飽和密度線の曲率に関わる臨界定数 \(\beta\) 。 |
他に臨界指数として知られているものについてみておくと、 定容熱容量についての臨界指数\(\alpha\)は\(T \gt T_C\)で臨界点に近づくのであれば、 \(c_v\)が密度によらないので0です(\(\alpha^{+}\)とされるもの)。 等温圧縮率については臨界密度で温度を下げて臨界点に近づくことを考えると
\begin{equation} \left( \frac{\partial P}{\partial \rho} \right)_T = \frac{T}{(1 - \rho_{\rm{c}})^2} - 2\rho_{\rm{c}} = \frac{9}{4} |\tau| \end{equation}
ですから臨界指数\(\gamma\) = 1です(\(\gamma^{+}\)とされるもの)。 また臨界指数\(\delta\) は臨界温度で密度を臨界密度に近づけていった時の圧力変化
\begin{equation} |P - P_{\rm {c}}| \propto |\rho - \rho_{\rm {c}}|^{\delta} \end{equation}
に相当するわけですが、式\eqref{eq:pexpand} を見ていただくと、 \(\tau = 0\) での圧力の密度の展開は3次から始まりますから\(\delta\) = 3です。