\[
\exp(-mgz/T)
\]
\[
\exp[-(m - m')gz/T]
\]
流体中の物体に浮力が働くこと、 また「物体が押しのける液体の重さに等しい浮力が働く」というアルキメデスの原理などは、 中学校までに教わります。 けれども浮力が分子についても働くのか、 いったいどれだけの浮力が働くのかについては、 大学でも正面切って議論されることはまずないでしょう。
|
\[
\exp(-mgz/T)
\]
|
\[
\exp[-(m - m')gz/T]
\]
|
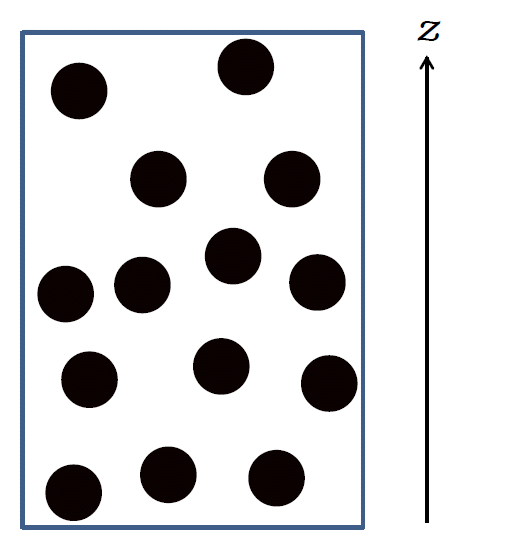
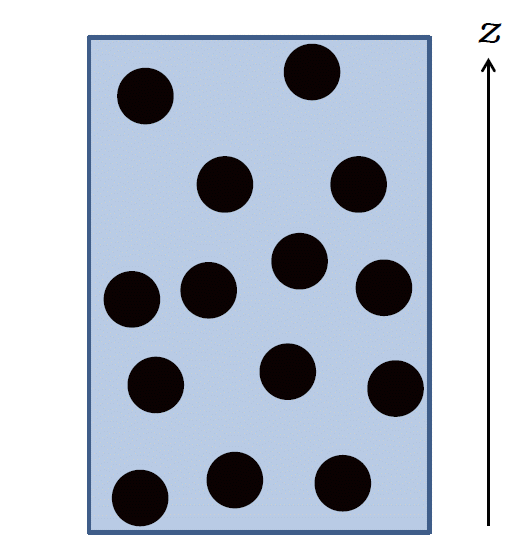
| 図 0-1. 測高公式とペランの実験。 気体中では浮力が働かないのに、 液体中では浮力が働く？ | |
たぶん大学の物理系の授業で、多くの学生がこの手の問題に出会うのは、 ボルツマン分布に関わって、いわゆる測高公式（hypsometric equation）とペランの実験が登場する時でしょう。 測高公式は大気圧から高度を得るもので、高度 \(z\) での密度 \(\rho(z)\) は次のように表されます：
\begin{equation} \rho(z) = \rho(0) \exp (-mgz/T) \label{eq:hypso} \end{equation}
ここで \(m\) は分子の質量、\(g\) は重力加速度、\(T\) は熱力学温度です。 後でも触れますが、このおはなしでは簡単のためボルツマン定数 \(k_\mrm{B}\)を 1 とします。 一方、分子の存在を実証した研究として著名なペラン Perrin の沈降平衡の実験で、 水中に分散させたコロイド粒子の沈降平衡を表す式はというと、 次のようになります：
\begin{equation} \rho(z) = \rho(0) \exp [-(m-m')gz/T) \label{eq:perrin} \end{equation}
ここで \(m'\) は「コロイド粒子が押しのける」流体の質量で、 アルキメデスの原理から \(m'g\) はコロイド粒子に働く浮力です。
演習などでこうした問題を解きはするものの、 コロイド粒子が小さくなり分子サイズになったらどうなるか、 ふと疑問に思う学生も多いのではないでしょうか？ もし測高公式 \eqref{eq:hypso} に浮力の補正を入れると、 アルキメデスの原理からは「分子が押しのける流体の重さに等しい」浮力が働くわけですが、 空気の分子の押しのける空気の重さは自身の重さです。 これでは重力と浮力が釣り合って、高度を上げても密度は変化しないことになってしまいます。 どこに問題があるのでしょう？ 自分自身に働く力を考えるからおかしいのでしょうか？ そもそも分子には異なる力学法則が働くのでしょうか？ ・・・・・・・
このおはなしではもっぱら一成分の流体について、 平衡状態で分子に働く浮力の問題を考えます。 何かの参考になれば幸いです。
目次