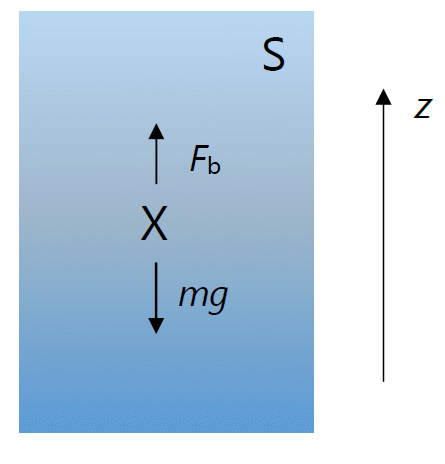
流体中の分子に働く浮力を考えようというわけですが、 何か捉えどころのない問題といえるかもしれません。 平衡状態にある流体中には巨視的な流れはなく、 分子に注目してみればランダムな運動はありますが、それを平均すれば分子の流れも 0 になっているはずです。 同様に流体に重力が働いていても、 それと釣り合う力が圧力勾配という形で働いていて、 平均すれば流体に働く力は 0 ですし、分子あたりに働く力も平均すれば 0 です。 まずはこの「流体に働く力」について、 少し冷めた目で考えてみましょう。
高度 \(z\) で流体に働く力 \(F(z)\) というのは、熱力学的に考えると、 化学ポテンシャル \(\mu(z)\) の勾配と関係づけて考えることができます。 平衡状態では、化学ポテンシャルは場所によらずに同じで、 上の「流体に働く力は平均すれば 0 になる」という話は、 次のように考えることができます。 なおこのおはなしでは、全編、温度 \(T\) 一定で考えているので、偏微分の際の条件(添字)の \(T\) は省略します。
\begin{eqnarray} -F(z) &=& \frac{\rmd \mu(z)}{\rmd z}\\ &=& \pdifA{\mu(z)}{z}{\rho} + \pdifA{\mu(z)}{\rho(z)}{z} \frac{\rmd \rho(z)}{\rmd z} = 0 \label{eq:thforce} \end{eqnarray}
密度が一定であれば化学ポテンシャルは位置エネルギー \(mgz\) だけ増えますから、 式 \eqref{eq:thforce} の第一項は \(mg\) であり、次式が得られます(\(\partial \mu/\partial P = \rho^{-1}\) に注意):
\begin{equation} mg + \frac{1}{\rho(z)} \pdifA{P(z)}{\rho(z)}{z} \frac{\rmd \rho(z)}{\rmd z} = mg + \frac{1}{\rho(z)} \frac{\rmd P(z)}{\rmd z} = 0 \label{eq:thforcex} \end{equation}
この式は、測高公式を導く際の圧力の釣り合いの式と同じです。 流体に働く力を熱力学的に検討してみても、 先に考えたのと同じ結果が得られます。 でもここで扱っている流体に働く力 \(F(z)\) は、 流体に働く力を単純に各分子に割り振ったもので、 分子の流入・流出といった問題は考慮していません。 必ずしも流体中の分子に働く力というわけではありません。
式 \eqref{eq:thforcex} で、少し精密に考えると \[ \frac{\rmd P(z)}{\rmd z} = \pdifA{P(z)}{\rho(z)}{z} \frac{\rmd \rho(z)}{\rmd z} + \pdifA{P(z)}{z}{\rho(z)} \] なわけですが、右辺第2項は、圧力が温度、密度の関数で、\(z\) にあらわに依存しないと考えているので 0 になります。
ここでは分子に働く力について考えるわけですが、 力に限らず、液体中の種々の現象について、たいていわれわれ化学者は、ある分子に乗って物事を見ています。 これは何気なく行われていることですが、 ちょうど均一な水中で、水分子の「拡散」を考えるのにも似ています。 均一ですから拡散は起きませんが、われわれはある水分子を特別視することで、水の拡散を考えます。 これを自己拡散(あるいはトレーサー拡散)と呼んでいますが、つまり自己と他者を弁別し、 1成分系でありながら、あたかも(一方の成分が無限希釈量の)2成分系だと考えているわけです。 このことを、あからさまに取り扱ってみましょう。
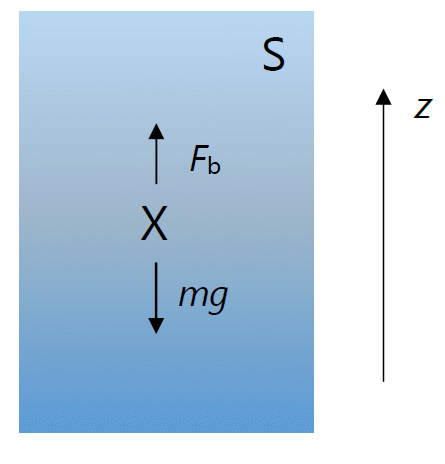
|
| 図 2-1. 溶媒 S の中に無限希釈量溶け込んだ、 S と化学的に同一の性質を持つ溶質分子 X。 X には重力 \(mg\) と、溶媒 S との相互作用により、 S の密度勾配に応じた浮力 \(F_\mrm{B}\) が働き、 X の密度(濃度)勾配が生まれます。 |
溶媒 S にごく微量、無限希釈量溶け込んだ、 溶質分子 X に働く力を考えます。 分子 X は溶媒分子 S と化学的には全く同等に振舞い、分子質量 \(m\) も同じであるものとします。 つまり X は、流体 S 中で、われわれが注目する分子というわけです。 この仮想的な分子種 X の化学ポテンシャルは、次のように表すことができます (温度 \(T\) について \(k_\mrm{B} = 1\) とする単位系を取っていることに注意):
\begin{equation} \mu_\mrm{X}(z) = \mu_\mrm{X}^\circ(z) + T \ln \rho_\mrm{X}(z) \label{eq:xcp} \end{equation}
ここで \(\circ\) は標準状態であることを示します。 ここでは標準状態として、単位体積中に1個の X 分子が存在する状態を考えます。
平衡状態で流体中の分子種 X に働く力は 0 です。 したがって標準状態の X に働く力 \(F^\circ_\mrm{X}(z)\) は X の密度分布 \(\rho_\mrm{X}(z)\) (「濃度分布」と呼びたいところですが、 溶媒同様に「密度分布」と呼ぶことにします)を用いて次のように表されます:
\begin{equation} -F_\mrm{X}(z) = \frac{\rmd \mu_\mrm{X}(z)}{\rmd z} = \frac{\rmd \mu_\mrm{X}^\circ(z)}{\rmd z} + T \frac{\rmd \ln \rho_\mrm{X}(z)}{\rmd z} = 0 \label{eq:xforcebalance} \end{equation} \begin{equation} F^\circ_\mrm{X}(z) = -\frac{\rmd \mu_\mrm{X}^\circ(z)}{\rmd z} = T \frac{\rmd \ln \rho_\mrm{X}(z)}{\rmd z} \label{eq:xforce} \end{equation}
ここで X の密度勾配が問題となりますが、 X は S と化学的には同等に振舞うと考えていますから、 平衡状態で X と S の組成比 \(\rho_\mrm{X}(z)/\rho_\mrm{S}(z)\) は高度 \(z\) によらず一定になり( \(\rmd \ln [\rho_\mrm{X}(z)/\rho_\mrm{S}(z)]/\rmd z = 0\) )、 両者の密度勾配の間には次の関係が成立します:
\begin{equation} \frac{\rmd \ln \rho_\mrm{X}(z)}{\rmd z} = \frac{\rmd \ln \rho_\mrm{S}(z)}{\rmd z} \label{eq:xdensgrad} \end{equation}
流体の密度勾配についての式 \eqref{eq:thforcex} を参照すると、 標準状態の X に働く力は次のように表せます:
\begin{equation} F^\circ_\mrm{X}(z) = -mgT \pdifA{\rho(z)}{P(z)}{z} = -mg \kappa_T(z) \rho(z) T \label{eq:xavecforce} \end{equation}
ここで \(\kappa_T\) は等温圧縮率 \(\rho_\mrm{S}^{-1} (\partial \rho_\mrm{S}/\partial P)\) です。 X には重力 \(mg\) が働いていますから、 それ以外の力は流体の密度勾配、圧力勾配によって生み出される力です。 これが分子 X に働く浮力 \(F_\mrm{b}\) に相当します。
\begin{equation} F^\circ_\mrm{X}(z) = -mg + F_\mrm{b}(z) = -mg + [v(z) - \kappa_T(z) T] \rho(z) mg \label{eq:xforcea} \end{equation}
ここで \(v(z)\) は分子あたりの体積 \(\rho^{-1}\) です。 高度 \(z\) についての引数を外した形で、改めて分子に働く浮力の表式を示すと次のようになります:
\begin{equation} F_\mrm{b} = (v - \kappa_T T) m\rho g = (1 - \rho \kappa_T T) mg \label{eq:bforcea} \end{equation}
こうしてみると、分子に働く浮力についてもアルキメデスの原理、 「浮力は物体が押しのける流体の重さに等しい」は成立するのですが、 その際の物体、分子が押しのける体積は \(v - \kappa_T T\)、 昔ぼくが論じた部分モル体積についての「配置の寄与」になっているわけです。
実際に気体と液体で、浮力がどう違うかを見積もってみると、 理想気体の等温圧縮率は \(1/P\) で、分子容は \(T/P\) ですから、配置の寄与は 0 であり、 気体中の浮力は 0。 液体に目を転じれば、常温常圧でエタノールやヘキサンなど、通常の溶媒のモル体積は 100 cm3/mol 程度とみてよく、 等温圧縮率は 1 GPa-1 ぐらいですから、\(\kappa_T T\) は 3 cm3/mol 程度。 われわれが通常目にする液体中の分子に働く浮力は、 分子に働く重力とだいたい釣り合っている、 分子はほとんど ”浮いている” と見てよいわけです。
液体論を齧ったことのある方のためにコメントしておくと、距離 \(r\) 離れた分子間の平均力 \(\avg{F(r)}\) (あるいは平均力ポテンシャル)と出会われたことがあるでしょう: \[ \avg{F(r)} = T \frac{\rmd \ln g(r)}{\rmd r} \] ここで \(g(r)\) は動径分布関数です。 動径分布関数の勾配を平衡状態での密度勾配と読み替えれば、分子間の平均力を与える関係式は、 式 \eqref{eq:xforce} と同等である(あるいは平均力ポテンシャルが標準状態の化学ポテンシャル \(\mu_\mrm{X}^\circ(z)\) と同等である)ことが見て取れるでしょう。
|
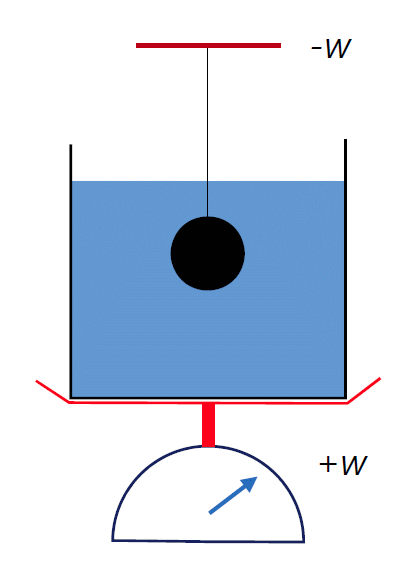
| 図 2-2. 浮力をはかるには、液体に浸した状態で、物体にかかる力の変化(-w)を調べてもよいし、 液体の重さの変化(+w)を調べてもよい。 |
先の節では溶媒 S に無限希釈量溶け込んだ、 化学的には溶媒 S と同じ性質を持つ溶質分子 X に注目して、 X 分子に働く力を分子種の密度勾配から評価して、 アルキメデスの原理に言う「分子が押しのける流体の重さ」を考えました。 ここでは X 分子が押しのける流体の重さに注目して、分子に働く浮力を考えてみましょう。 巨視的な実験に準じていえば、物体に働く浮力を測るのに、 物体を紐で吊るして、容器に満たした溶媒に浸した時に、 物体を吊るした紐にかかる荷重の変化を見てもよいし、 容器の重さの変化を調べてもよいわけです。 ここではこの容器の重さの変化を調べる立場といっていいでしょう。
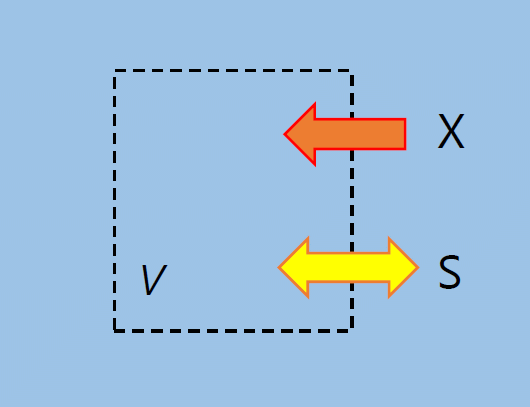
さて分子 X が押しのける流体の重さというのは、 体積 \(V\) の容器に X を入れた時に、容器から出てくる溶媒 S の量を見ればよいわけですが、 どのような条件で X を入れるかに注意が必要です。 挿入する X 分子は、自由に動き回らないように固定しておく必要があります (先に X に働く力を考えた際には、X が溶液中に平衡分布して重力下、濃度勾配を持つことになっていました)。 これはいわば、S 分子は通すが X 分子を通さない半透膜の箱に X を閉じ込めておくようなものです。 つまり、S の化学ポテンシャルを一定にした条件で、体積 \(V\) を一定にした半透膜で区切られた領域に X を入れた時の、 S 分子の出入りを評価することになるわけです。 この S 分子の出入りを評価するには、次式のように一端、 粒子数一定の条件の下での体積変化の比の形に書き換えた方が、手になじんだ圧力、体積を用いた表現に持ち込むことができ、 見通しがよいようです。
|
| 図 2-3. 溶媒 S は通すが X は通さない半透膜で囲われた中に、 X 分子を挿入した際の S 分子の出入りを考えます。 |
\begin{equation} \pdifA{N_\mrm{S}}{N_\mrm{X}}{V, \mu_\mrm{S}} = -\pdifA{N_\mrm{S}}{V}{N_\mrm{X}, \mu_\mrm{S}} \pdifA{V}{N_\mrm{X}}{N_\mrm{S}, \mu_\mrm{S}} = -\rho \pdifA{V}{N_\mrm{X}}{N_\mrm{S}, \mu_\mrm{S}} \label{eq:exchangex} \end{equation}
ここで \((\partial V/\partial N_\mrm{S})_{\mu_\mrm{S}, N_\mrm{X}} = (\partial V/\partial N_\mrm{S})_{P, N_\mrm{X}} = V/N_\mrm{S} = \rho^{-1}\) であることを用いました。 ここで問題になるのは \((\partial V/\partial N_\mrm{X})_{N_\mrm{S}, \mu_\mrm{S}}\) で、 圧力 \(P\) 一定での微分であれば X の部分モル体積ですが (「部分分子体積」と呼んだ方が良いかもしれませんが、なじみのある呼称で通します)、溶媒の化学ポテンシャル \(\mu_\mrm{S}\) 一定の条件では、 話は変わってきます:
\begin{equation} \pdifA{V}{N_\mrm{X}}{\mu_\mrm{S}, N_\mrm{S}} = \pdifA{V}{N_\mrm{X}}{P, N_\mrm{S}} + \pdifA{V}{P}{N_\mrm{X}, N_\mrm{S}} \pdifA{P}{N_\mrm{X}}{\mu_\mrm{S}, N_\mrm{S}} \label{eq:cvolx} \end{equation}
ここで右辺第1項は X の部分モル体積であり、 X は溶媒 S と化学的に同一の性格を持つので S の部分モル体積、モル体積 \(v = \rho^{-1}\) に等しくなります。 そして右辺第2項の \(\partial P/\partial N_\mrm{X}\) は、X を挿入したことによる圧力変化、 浸透圧 \(T/V\) の発生に対応します。 式を整理すると次のようになります:
\begin{eqnarray} \pdifA{V}{N_\mrm{X}}{\mu_\mrm{S}, N_\mrm{S}} &=& V_\mrm{X} + \pdifA{V}{P}{N_\mrm{X}, N_\mrm{S}} \frac{T}{V} \\ &=& v - \kappa_T T \label{eq:cvol} \end{eqnarray}
ここで \(\kappa_T\) は等温圧縮率 \(-V^{-1} (\partial V/\partial P)\) です。 アルキメデスの原理からすると、浮力は X が押しのける S の重さになるわけですが、 式 \eqref{eq:exchangex} より、次のように表され
\begin{equation} F_\mrm{b} = -\pdifA{N_\mrm{S}}{N_\mrm{X}}{V, \mu_\mrm{S}} mg = \rho (v - \kappa_T T) mg = (1 - \rho \kappa_T T) mg \label{eq:bforceb} \end{equation}
先に濃度勾配から評価した X の浮力の表式、式 \eqref{eq:bforcea} と一致することがわかります。
ここでは詳しく述べませんが、化学ポテンシャルを一定にした下での、粒子数変化に対する体積の応答を表す式 \eqref{eq:cvol} は、 液体論でよく知られた圧縮率方程式 \[ \rho \kappa_T T = 1 + \rho \int {(g(r) - 1 ) \rmd \vec{r}} \] に対応しています。ここで \(g(r)\) は動径分布関数です。
分子に働く浮力の表式を得たので、 具体的に浮力が高度、密度とともにどう変化するかを、ファンデルワールス流体について見てみましょう。 問題となるのは \(\rho \kappa_T T\) という項ですが、 この項にはさまざまな顔があります。 この項は、 粒子数の揺らぎ(あるいは濃度、体積の揺らぎ)として理解できますし、 部分モル体積に対する「並進運動の寄与」の度合と捉えることもできます。
|
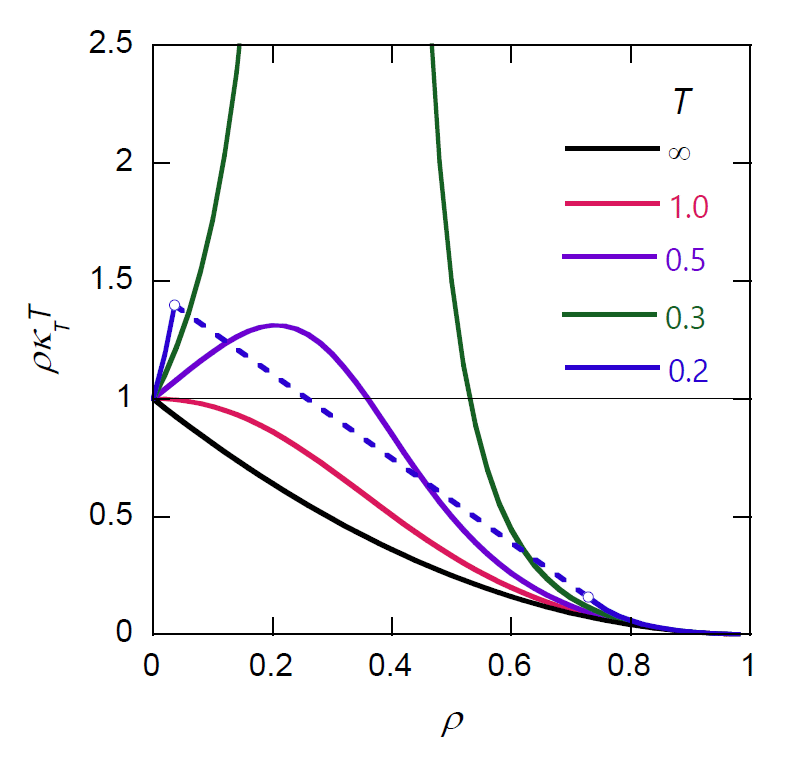
| 図 2-4. ファンデルワールス流体における、 種々の温度における部分モル体積に対する並進運動の寄与 \(\rho \kappa_T T\) の密度依存性。 \(T = 0.2\) では密度が \(0.036 \lt \rho \lt 0.729\) の範囲では気液の相分離が起きます。 |
この部分モル体積に対する並進運動の寄与 \(\rho \kappa_T T\) は、 相が安定(機械的安定性)であれば正であり、 理想気体では 1 で、高密度では 0 に漸近します。 また一般に、密度一定では温度の低下とともに増加し、 臨界温度以下では気液の相分離にともなって発散します (この話では固相の存在や、過冷却、過熱状態は考慮しません。 また系中に気液2相が共存する状態では、等温圧縮率は発散します)。 ですから気体から液体へ密度を増加させた時、十分温度が高ければ、\(\rho \kappa_T T\) は 1 から 0 へと単調に減少しますが、 温度が低くなると、単調でない挙動が現れます。
先の章でも触れたファンデルワールス流体について、 \(\rho \kappa_T T\) をあらわに書き下すと次のようになります:
\begin{equation} \rho \kappa_{T} T= \frac{T(1 - \rho)^2}{T - 2\rho (1 - \rho)^2} \label{eq:dkt_vdw} \end{equation}
図 2-4 にいくつかの温度について、ファンデルワールス流体の \(\rho \kappa_T T\) の密度依存性の挙動を示しました。 式 \eqref{eq:dkt_vdw} からも明らかに、 温度低下とともにファンデルワールス流体の部分モル体積に対する並進運動の寄与 \(\rho \kappa_T T\) は増加します。 高密度では相分離が生じるので明瞭ではありませんが、 温度低下にともなう \(\rho \kappa_T T\) の増大は、低中密度領域で顕著に認められます (臨界密度 \(\rho_\mrm{c} = 1/3\) では臨界温度 \(T_\mrm{c} = 8/27\) に向かって発散する形になります)。 これにともなって、ボイル温度以下では密度依存性も単調ではなくなり、 \(\rho \kappa_T T\) は 1 以上になり、極大を持つようになります (ファンデルワールス流体のボイル温度 \(T_\mrm{B}\) は \(1\) です)。 そして \(\rho \kappa_T T\) が 1 以上になると、 式 \eqref{eq:bforcea}、式 \eqref{eq:bforceb} から明らかに、浮力は負になり、いわば「沈力」として働くようになります。
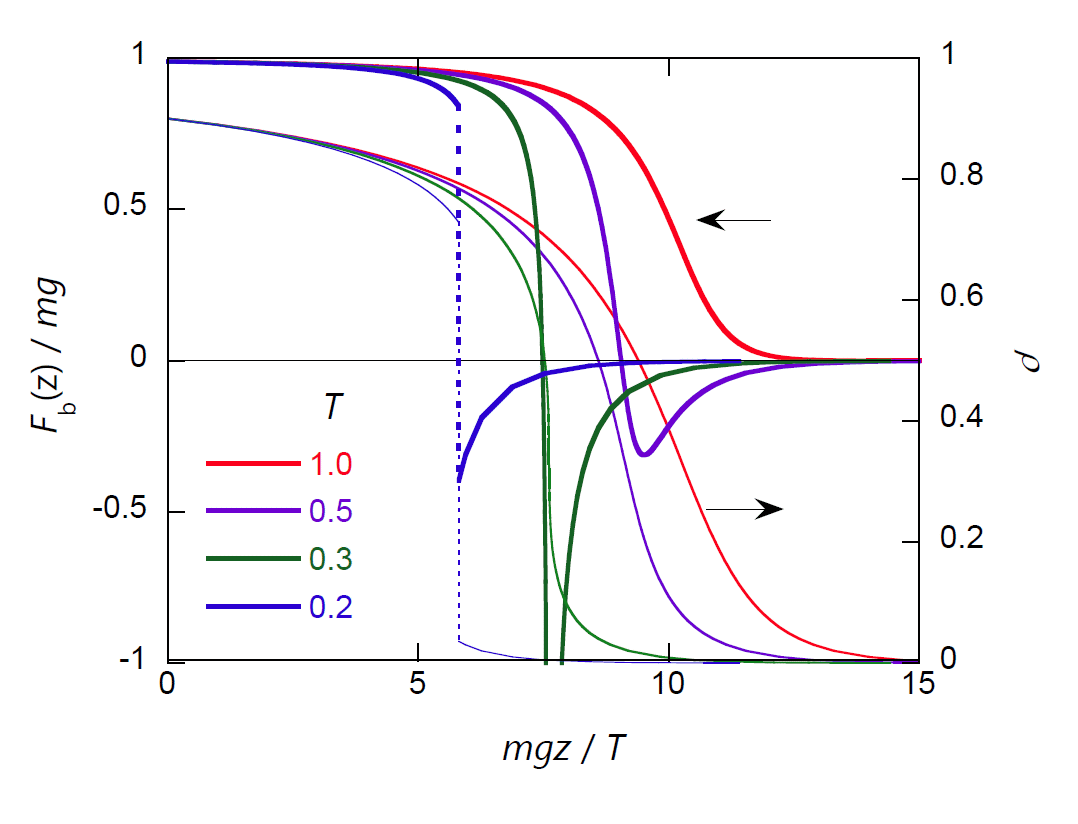
この部分モル体積に対する並進運動の寄与 \(\rho \kappa_T T\) の挙動を踏まえ、 前章で見た密度分布に対応させる形で、 図 2-5 では分子に働く浮力の高度による変化を見てみました。 分子に働く浮力と、密度勾配の間には次の関係が成り立っています:
\begin{equation} F_\mrm{b} (z) = T \frac{\rmd~\ln \rho(z)}{\rmd~z} + mg \label{eq:bf_gradd} \end{equation}
ですから密度勾配が十分大きいと、浮力が「沈力」になるわけで、 実際、気液の相分離近くの、密度勾配が大きい時に大きな「沈力」が働くことが見て取れます。 臨界点近傍の流体の実験では、しばしば重力による密度勾配の影響が問題になります。 こうした現象を解釈する上で、それは分子に「沈力」が働くためであると解釈する事も可能なわけです。
|
| 図 2-5. いくつかの温度における、 ファンデルワールス流体中の分子に働く浮力の高度 \(z\) 依存性。 細い線は密度依存性を示します。 温度がボイル温度より低いと(\(T \lt 1\))、浮力が「沈力」になる領域が存在します。 |