１．重力の下での流体の平衡密度分布

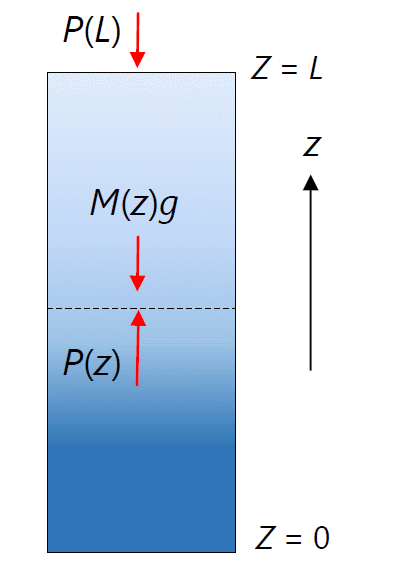
図 1-1. 重力下の流体中の力の釣り合い。 高さ \(L\) の単位断面積の円筒を考えると、高さ \(z\) より上方の流体については、 上からの圧力 \(P(L)\) と流体に働く重力 \(M(z)g\) が、下からの圧力 \(P(z)\) と釣り合っている。

１-１．重力下の流体の平衡

重力が働く液体中、平衡状態で密度がどう分布するかについて考えましょう。 鉛直方向に \(z\) 軸を取り、流体には一様な重力が働き、物体には鉛直下向きに一定の重力加速度 \(g\) が及ぼされるものとします。 流体を構成する分子の質量を \(m\) とすると、分子は \(-z\) 方向に \(mg\) だけの力を受けて、 運動することになります。

平衡状態で、流体の温度 \(T\) は高さ \(z\) によらず均一になります。 一方、圧力 \(P\)、数密度 \(\rho\) は 下方の圧力・密度が高く、 上方の圧力・密度が低くなります。 単位断面積で高さ \(L\) の円筒を考え、その中での力の釣り合いを考えると、次の関係が成り立ちます：

\begin{equation} P(z) = P(L) + M(z)g \label{eq:fbalance} \end{equation}

ここで \(M(z)\) は高さ \(z\) より上方の流体の質量で、次式で与えられます：

\begin{equation} M(z) = \int_z^L {m\rho(z') \rmd z'} \label{eq:fmass} \end{equation}

これを微分形で表現すると、次の圧力の釣り合いの式が得られます：

\begin{equation} \frac{\rmd P(z)}{\rmd z} = -m \rho(z) g \label{eq:pbalance} \end{equation}

ですから圧力と密度の関係式、状態方程式が与えられれば、 圧力、あるいは密度の高度 \(z\) 依存性が評価できることになります。

式 \eqref{eq:pbalance} は流体力学のオイラーの運動方程式 \[ m\rho \frac{\mrm{D} \vec{v}}{\mrm{D} t} = \rho \vec{K} - \mrm{grad}~ P \] で、流速 \(\vec{v}\) の時間依存のない場合に相当します（\(\vec{K}\) は分子１個当たりに働く外力。オイラーの平衡の式）。

１-２．測高公式 ―― 圧力の釣り合いとボルツマン分布

流体密度の高度依存性を表すものとして、よく知られた大気についての測高公式 hypsometric equation を見てみましょう。 理想気体の状態方程式は、次式のように表現できます。

\begin{equation} P = \rho T \label{eq:igaseos} \end{equation}

ここで \(\rho\) は数密度、\(T\) は熱力学温度です。 このお話では全編通じて温度は高さによらず一定であるとし、 最初にも触れましたが、簡単のためボルツマン定数 \(k_\mrm{B}\)（= 1.380649 ×10^-23 J K^-1）を 1 とします。 温度 \(T\) はエネルギーの次元を持ち、 \(k_\mrm{B} = 1\) とした、あるいは \(k_\mrm{B}T\) を \(T\) と表記していると見てもらってもよいでしょう。 1 気圧（約 0.1 MPa）、300 K の気体であれば、 \(T\) はおよそ 4 ×10^-21 J、 \(\rho\) は 2.4 ×10²⁵ m^-3 になります。 理想気体の状態方程式、式 \eqref{eq:igaseos} を先の式 \eqref{eq:pbalance} に入れると次式が得られ

\begin{equation} T \frac{\rmd P(z)}{\rmd z} = -m P(z) g \label{eq:hypsode} \end{equation}

ここから圧力と高度の関係式、測高公式を得ることができます。

\begin{equation} \frac{P(z)}{P(0)} = \exp{\lpar{-\frac{mgz}{T}}} = \exp{\lpar{-\frac{z}{H}}} \label{eq:hypso} \end{equation}

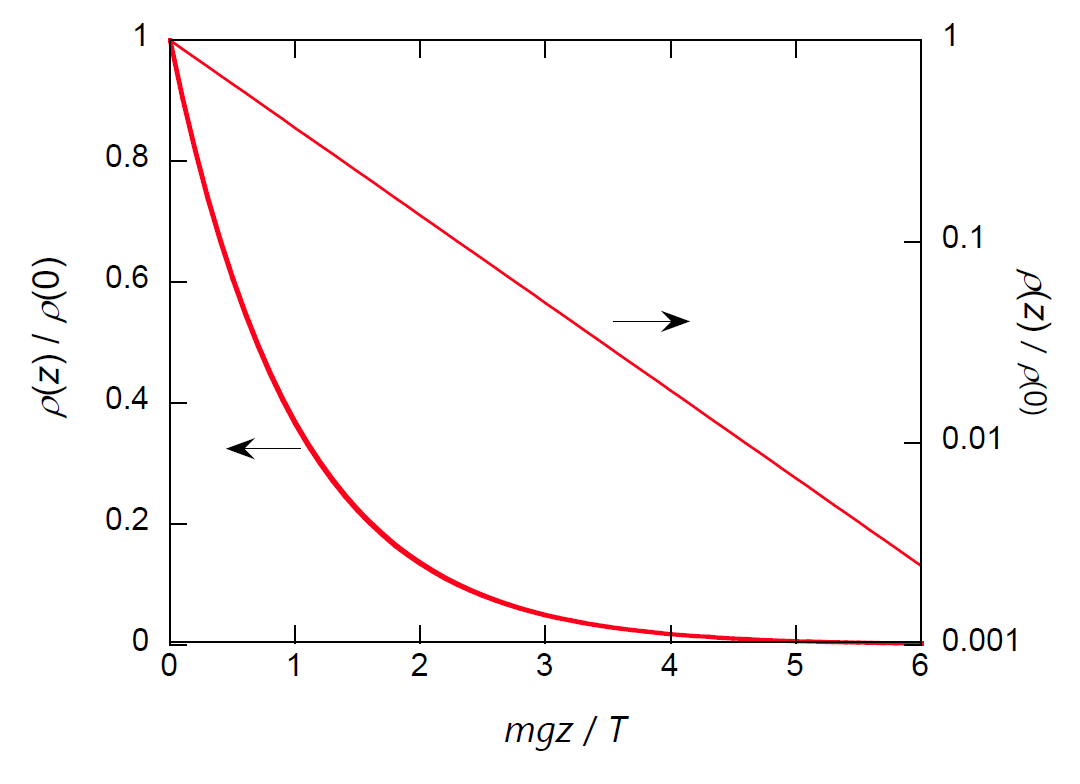
図 1-2. 測高公式から得られる密度分布。

ここで \(H = T/mg\) というのはスケールハイト scale height と呼ばれ、 気温を 290 K、モル質量を 30 g/mol、重力加速度 \(g\) 10 m s^-2 とすると 8.3 J/(mol K) × 290 K/ (0.03 kg/mol × 10 m s^-2) ∼ 8 km ぐらいになります。 大気科学ではよく用いられますが、今回のお話では、温度、重力の影響を明示するため、用いない方針で行きます。 また大気は完全な平衡状態にはなく、気温の高度依存性が問題になりますが、このおはなしでは一切考えません。

重力場のもとでのボルツマン分布から、測高公式を導くのも、 たぶん皆さんおなじみでしょう。

\begin{equation} \frac{\rho(z)}{\rho(0)} = \frac{P(z)}{P(0)} = \exp{\lpar{-\frac{mgz}{T}}} \label{eq:boltz} \end{equation}

図 1-2 には式 \eqref{eq:boltz} から得られる密度分布を示しました。 気体の平衡密度は高度の増加にともなって急速に減少していきます。

圧力の釣り合いからも（式 \eqref{eq:hypso}）、ボルツマン分布からも（式 \eqref{eq:boltz}）同じ密度分布が得られるわけですが、 空気がおおむね窒素と酸素の 4:1 の混合気体であることに注意すると、 ボルツマン分布から得られる式は \[ \rho(z) = \rho_\mrm{N_2}(0) \exp{\lpar{-\frac{m_\mrm{N_2}gz}{T}}} + \rho_\mrm{O_2}(0) \exp{\lpar{-\frac{m_\mrm{O_2}gz}{T}}} \] となって、単純な指数関数にはなりません。 あるいは \[ \frac{\rho_\mrm{O_2}(z)}{\rho_\mrm{N_2}(z)} = \frac{\rho_\mrm{O_2}(0)}{\rho_\mrm{N_2}(0)} ~\exp{\left[-\frac{(m_\mrm{O_2} - m_\mrm{N_2})gz}{T}\right]} \] となって、組成が高度とともに変化することになります。 このような組成の変化に踏み込んだ考察には（ボルツマン分布では暗黙の内に考慮されている）化学ポテンシャルを考えることが必要で、 圧力の釣り合いだけでは評価できません。 なおこうした組成の変化は同位体分離とも関わって興味深い問題ですが、 拡散速度は圧力の緩和に比べて極めて遅く、大気では観察されません。

１-３．化学ポテンシャルの釣り合いと密度分布

先には圧力の釣り合いから密度分布を考えたわけですが、 化学ポテンシャルからも密度分布を得ることができます。 またここでは１成分系を考えていますが、化学ポテンシャルからは多成分系についても、 その平衡分布を評価することもできます。

平衡状態では化学ポテンシャルは温度同様、 高度によらず一定になっていますから次式が成り立ちます：

\begin{equation} \mu(\rho(z), z) = \mu(\rho(0), 0) \label{eq:cpbalance} \end{equation}

ここで化学ポテンシャルの密度 \(\rho\)、高度 \(z\) 依存性を明示するため、 化学ポテンシャルを \(\mu(\rho(z), z)\) と表記しています。 この一方、密度が同じであれば、化学ポテンシャルは位置エネルギー \(mgz\) だけ大きくなり、 次式が成り立ちます：

\begin{equation} \mu(\rho(z), z) = \mu(\rho(z), 0) + mgz \label{eq:cppot} \end{equation}

したがって、化学ポテンシャルと密度の関係が分かっておれば、 次式から高度 \(z\) における密度 \(\rho(z)\) が分かることになります。

\begin{equation} \mu(\rho(z), 0) = \mu(\rho(0), 0) - mgz \label{eq:cpden} \end{equation}

圧力の釣り合いを表す式 \eqref{eq:pbalance} は、この関係式の微分形に相当します （温度を一定であるとしているので、偏微分の際の条件（添字）に温度を書くのは省略します。 \(\partial \mu/\partial P = 1/\rho\) であることに注意）：

\begin{equation} \frac{\rmd \mu(\rho(z), 0)}{\rmd z} = \pdif{\mu(\rho(z), 0)}{P(z)} \frac{\rmd P(z)}{\rmd z} = \frac{1}{\rho(z)} \frac{\rmd P(z)}{\rmd z} = - mg \label{eq:cpden_v} \end{equation}

１-４．重力下でのファンデルワールス流体の密度分布

浮力を考える状況では分子が互いに押し合いへし合いしているでしょうから、 理想気体に止まらず、流体が液化したりする状況を考慮する必要があるでしょう。 そうした流体として、ファンデルワールス状態方程式にしたがう流体（ファンデルワールス流体）について、 どのような密度分布が得られるか見てみましょう。 ファンデルワールス状態方程式は次のように書けます：

\begin{equation} P = \frac{\rho T}{1- \rho} - \rho^2 \label{eq:vdw_eos} \end{equation}

ここではファンデルワールスのパラメーター、\(a\) と \(b\) を 1 としています。 ですから臨界定数はそれぞれ次のようになります：

\begin{equation} T_\mrm{c} = 8/27,~~P_\mrm{c} = 1/27,~~\rho_\mrm{c} = 1/3 \label{eq:vdw_crpara} \end{equation}

このファンデルワールス状態方程式から、化学ポテンシャルの表現として次式が得られます：

\begin{equation} \mu = \mu^*(T) + \frac{T}{1- \rho} + T \ln \frac{\rho}{1 - \rho} - 2\rho \label{eq:vdw_cp} \end{equation}

ここで \(\mu^*(T)\) は、密度に依存しない関数です。 すると高度 \(z = 0\) における流体の密度 \(\rho(0)\) が与えられれば、 高度 \(z\) における密度は、次式を解くことで得られます：

\begin{equation} \mu(\rho(z)) = \mu(\rho(0)) - mgz \label{eq:vdw_densdist} \end{equation}

十分密度が低ければ、化学ポテンシャルは次式のように表され

\begin{equation} \mu \approx \mu^*(T) + T + T \ln \rho \label{eq:vdw_cpx} \end{equation}

先の測高公式が得られます：

\begin{eqnarray} \mu(\rho(z)) - \mu(\rho(0)) &=& T \ln \rho(z)/\rho(0)\\ &=& - mgz \label{eq:vdw_densdistx} \end{eqnarray}

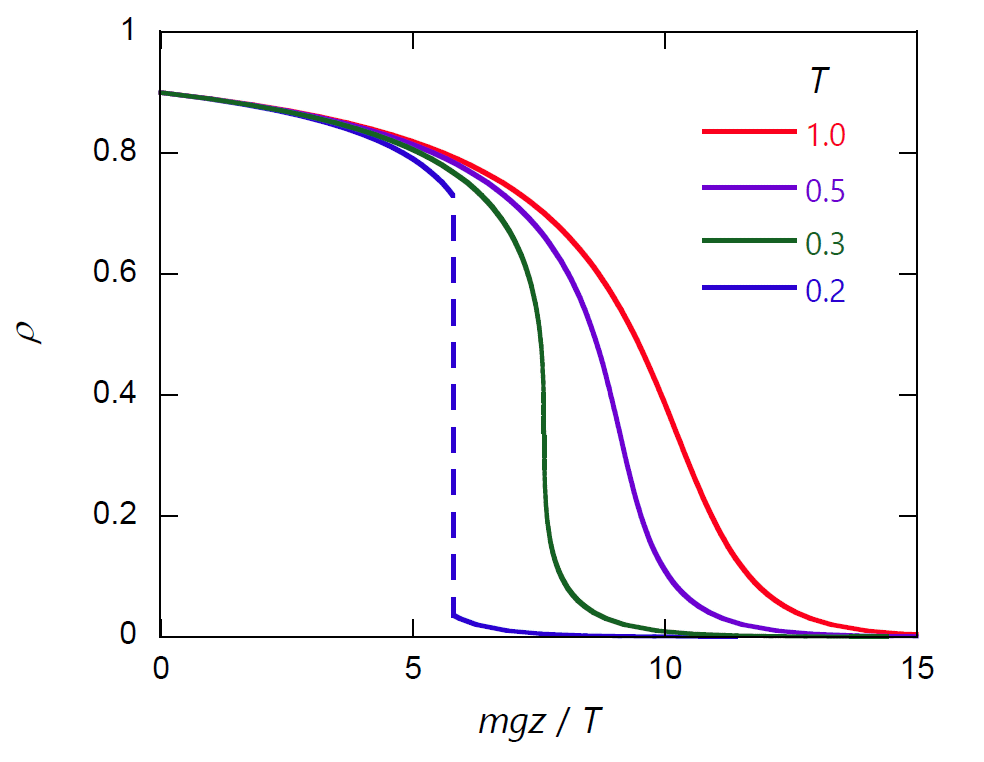
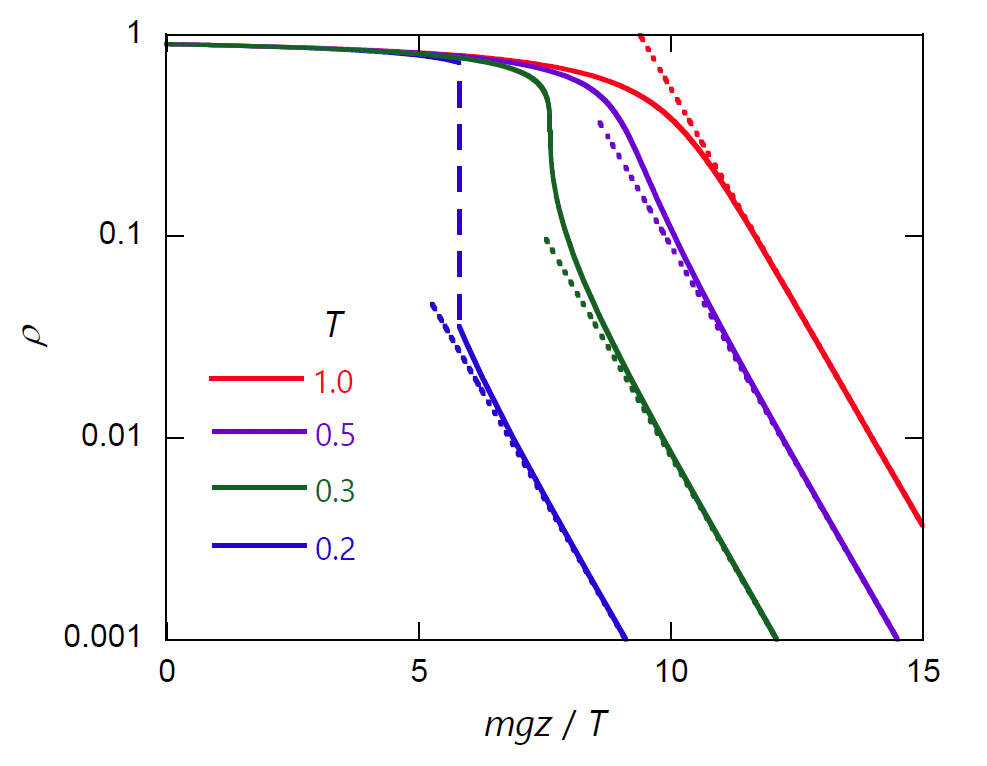
密度の増加、温度の低下とともに、測高公式からの偏倚は大きくなり、 特に臨界温度 \(T_\mrm{c} = 8/27 ~(= 0.296\ldots)\) 以下では、気液の相分離が起きるようになります。 図 1-3 には高度 \(z = 0\) の密度を \(\rho = 0.9\) とした場合の、 種々の温度での密度の高度依存性を示しました。 \(T = 0.2 \lt T_\mrm{c}\) の場合、\(mgz/T = 5.81\) で \(\rho = 0.036\) の蒸気と\(\rho = 0.729\) の液体に相分離が起きています。 これを現実の物質でいうと、ガスライターに使われるブタンだと、臨界温度が 425 K で、臨界密度が 0.228 g/cm³、モル質量が 58 g/mol ですから、 温度 T = 0.2 はほぼ室温の 290 K、密度 ρ = 0.9 は 0.62 g/cm³ に対応します（290 K のブタンの液相の飽和密度は 0.58 g/cm³）。 温度 290 K では、\(mgz/T = 5.81\) は \(gz = 2.4 \x 10^5~ \mrm{m^2~s^{-2}}\) に相当します。 仮に z = 10 cm とすると g は 25 万 G で、通常の遠心分離を考えると、ケタ違いに大きな重力加速度が必要になる（超遠心分離）勘定になります。

図 1-3a. 重力の下でのファンデルワールス流体の密度分布（\(\rho(0) = 0.9\)）。 \(T = 0.2\) では、気液の相分離が起きています（\(T_\mrm{c} = 8/27 = 0.296\ldots\) ）。	図 1-3b. 対数スケールで表した重力の下でのファンデルワールス流体の密度分布（\(\rho(0) = 0.9\)）。 点線は測高公式、式 \eqref{eq:boltz}から得られる密度分布。

また十分密度が高ければ、化学ポテンシャルは次式のように表され

\begin{equation} \mu \approx \mu^*(T) + \frac{T}{1- \rho} \approx \mu^*(T) + P/\rho \label{eq:vdw_cpy} \end{equation}

式 \eqref{eq:vdw_densdist} から、圧力が深度に比例するという、 水圧や地圧でよく見られる関係式がえられます（\(\rho \simeq 1\) としています）：

\begin{equation} P(z) - P(0) \approx - mgz \label{eq:vdw_pressdisty} \end{equation}

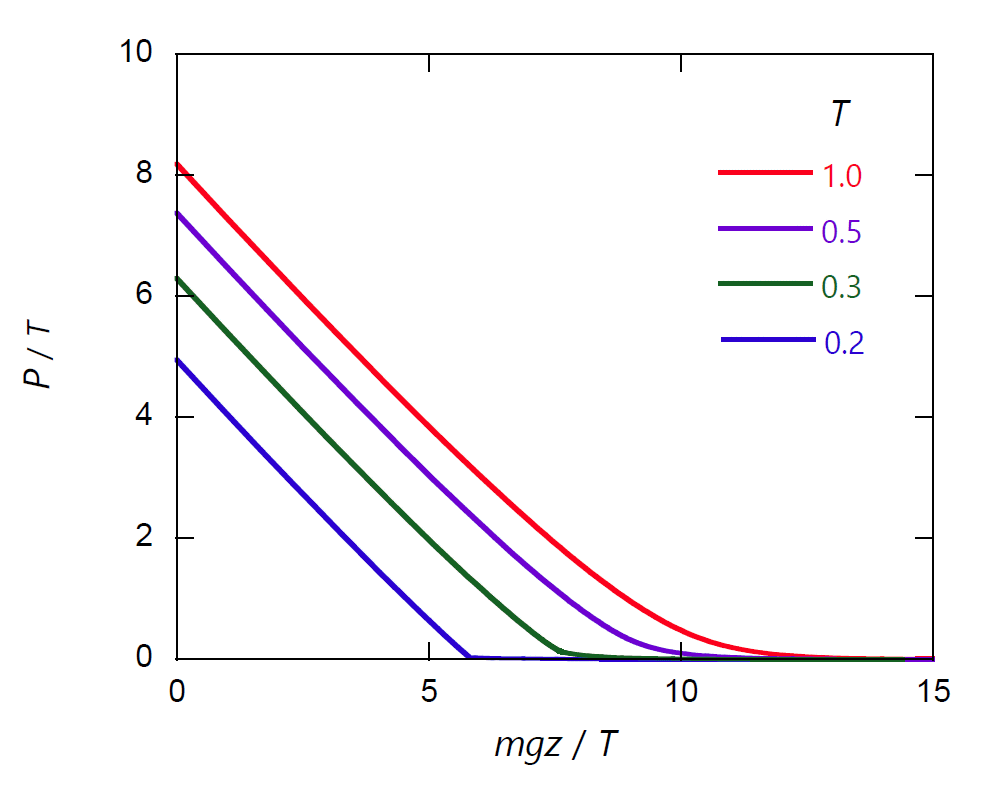
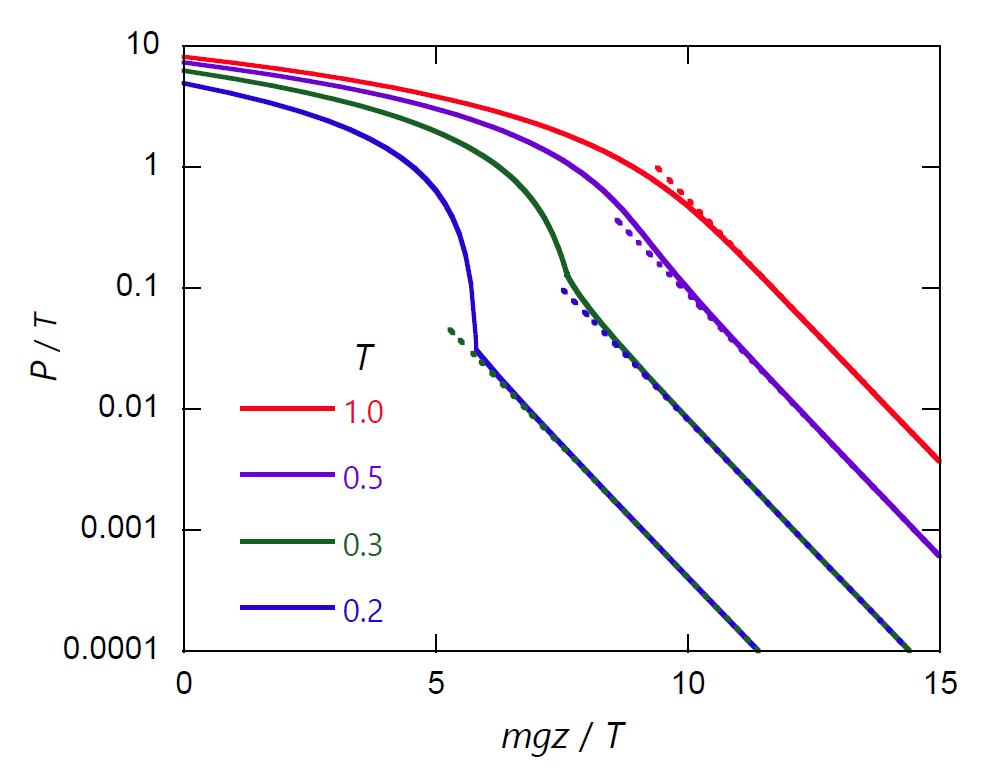
実際、図 1-4 に示すように、 圧力は高密度側で高度 \(z\) の増加にともない直線的に減少し、 低密度側では測高公式、式 \eqref{eq:boltz} に見るように、 指数関数的に減少するようになります。

図 1-4a. 重力の下でのファンデルワールス流体の圧力分布。 高密度域では、高度 \(z\) の減少とともにほぼ直線的に圧力が増加していきます。 \(z = 0\) で \(\rho = 0.9\) になるように設定しているので、 \(z = 0\) で \(P/T = 9 - 0.9/T\) になります。	図 1-4b. 対数スケールで表した重力の下でのファンデルワールス流体の密度分布。 点線は測高公式、式 \eqref{eq:boltz}から得られる圧力分布。 \(T = 0.2 \lt T_\mrm{c}\) では、\(P/T = 0.31\) で気液の相分離が起き、 等温線の勾配が不連続になります。

表紙のページへ