ここまで見てきた話は、基本、熱力学的な考察にもとづくもので、 分子論的な側面はあまり表舞台に出てきませんでした。 ここでは気体分子運動論的な立場から、希薄な気体、特に剛体球分子、パチンコ玉からなる気体に注目して、 流体に働く力と、分子に働く力・浮力を眺めてみることにしましょう。
分子間ポテンシャル \(u(r)\) が次式で与えられる、質量 \(m\)、直径 \(\sigma\) の剛体球分子、パチンコ玉からなる希薄な気体を考えます。 熱力学温度 \(T\) は一定とし、ここまで同様ボルツマン定数を単位に取ります(\(k_\mrm{B} = 1\))。 また分子の数密度 \(\rho\) は十分小さく、剛体球同士の複雑な衝突・相互作用は考えなくてよいものとし、 剛体球は完全弾性体で、ツルツルしている(衝突の際、偶力が働かない)とします。
\begin{equation} u(r) = \left\{ \begin{array}{rl} \infty & r \lt \sigma\\ 0 & r \ge \sigma \end{array} \right . \label{eq:hs} \end{equation}
分子運動論から、分子の速度 \(\vec{v}\) の分布関数 \(f(\vec{v})\) は次式で与えられます:
\begin{equation} f(\vec{v}) = \left( \frac{m}{2\pi T} \right)^{3/2} \exp \left [-\frac{m\vec{v}^2}{2T}\right ] \label{eq:maxwell} \end{equation}
分子の速度分布は等方的で、分子質量と温度によって決まり、密度に依存しません。 初歩の気体分子運動論で学ぶことですが、気体分子が壁面に、単位面積、単位時間当たりに伝える運動量が圧力に相当します。 もう少し一般化すると、圧力は単位時間、単位面積あたりに流入・流出する運動量、運動量の流束と見なせるわけです。 ここではまず流体中の \(z\) 軸に垂直な面について、この運動量の出入りを考えてみましょう。
流体の運動量を担っているのは、その質量を担っている個々の分子です。 分子の流れ、流束について、単位面積当たり、単位時間に \(z\) 方向に流れる速度 \(\vec{v}\) の分子数 \(j_z(\vec{v})\) は次式で与えられます:
\begin{equation} j_z(\vec{v}) = \rho v_z \label{eq:p_fluxa} \end{equation}
平衡状態でこの粒子数の流れを分子の速度分布に対して平均化すれば 0 になります(\(\avg{\vec{v}} = 0\))。 けれども運動量の流れ \(p_z = mv_z j_z(\vec{v})\) の平均は 0 ではなく、 単位面積当たりに働く力、圧力 \(P\) になります。
\begin{equation} P = \avg{m v_z j_z(\vec{v})} = m \rho \int_{-\infty}^\infty v_z^2 f(v_z) \rmd v_z = \rho T \label{eq:p_idx} \end{equation}
こうして理想気体の状態方程式が導かれます。 またこの導出過程からも明らかに、平衡状態の流体中では \(x, y, z\) どの向きを取っても運動量の流れ、 圧力は方向によって大きさ、符号が変化せず等方的です(流体力学のパスカルの原理)。
さてここに \(z\) 方向に重力 \(-mg\) が働くものとします。 すると運動量の流れ \(m \rho(z) v_z^2\) に注目すると、 運動量の流れの変化は重力に対応しますから、次式が成り立ちます(運動量の流れに対する連続の式):
\begin{equation} \frac{\rmd m \rho(z) v_z^2}{\rmd z} = -m \rho(z) g \label{eq:pcont1} \end{equation}
速度についての平均を取ると式 \eqref{eq:p_idx} に見るように \(\avg{v_z^2} = T/m\) であり、 次の測高公式を導く際の圧力の釣り合いの式が得られます:
\begin{equation} \frac{\rmd P(z)}{\rmd z} = -m \rho(z) g \label{eq:p_balance} \end{equation}

|
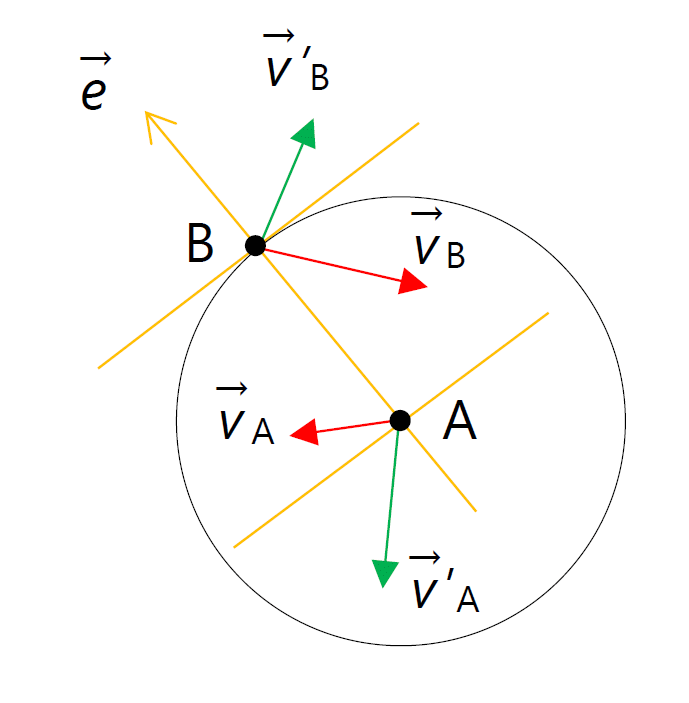
| 図 3-1. 剛体球 A への B の衝突(2次元的な模式図)。 A を中心とする半径 \(\sigma\) の球(排除球)の面上で B との衝突は起きます。 衝突に際しては、A から B を見る方向の単位法線ベクトル \(\vec{e}\) に沿った速度成分 (上付き \(\perp\) で示す)の交換が起き、 A から見ると排除球の表面に \(\rho T\) の圧力が及ぼされることになります。 |
前節では運動量の流れから、分子間相互作用がなくとも流体に力が働くことを見ました。 では流体を構成している剛体球、パチンコ玉に働く力はどうなるでしょう。 少していねいに(くどく)、事情を追ってみましょう。
2個のパチンコ玉 A と B の位置を \(\vec{r}_\mrm{A}\)、\(\vec{r}_\mrm{B}\) とし、 A から B の方位を示す単位ベクトルを \(\vec{e}\) とします。 パチンコ玉の相対位置 \(\vec{r}_\mrm{AB} = \vec{r}_\mrm{B} - \vec{r}_\mrm{A}\) が接触距離にある時 (\(\vec{r}_\mrm{AB} = \sigma \vec{e}\) )、 A と B の相対速度 \(\vec{v}_\mrm{AB} = \vec{v}_\mrm{B} - \vec{v}_\mrm{A}\) が、 距離が縮まる向きを向いておれば( \(\vec{v}_\mrm{AB} \cdot \vec{e} \lt 0\)) A と B の衝突が起きます。 衝突の起きるこの半径 \(\sigma\) の球を排除球、 その体積を排除体積と呼びます。 A から見て B のパチンコ玉の中心は排除球の内部に入れませんが、A と B の排除球同士の重なりは起きることに注意します。 パチンコ玉は完全弾性体で、ツルツルしていると考えているので、 衝突の際の撃力は排除球の接面の法線方向 \(\vec{e}\) に働き、 衝突後の速度 \(v'\) について、接面に平行な成分については変化がなく、 接面の法線方向の成分について、A と B で交換が起きます:
\begin{eqnarray} (\vec{v'}_\mrm{A})^\perp &=& (\vec{v}_\mrm{B})^\perp \\ (\vec{v'}_\mrm{B})^\perp &=& (\vec{v}_\mrm{A})^\perp \label{eq:changevel} \end{eqnarray}
ここで上付き \(\perp\) は排除球の接面の法線方向成分を示します。
さて A を中心とする排除球の接面に垂直方向の運動量の流れ \(p_\mrm{c}\) に注目すると、 衝突に際して流入する運動量と流出する運動量があるので
\begin{eqnarray} p_\mrm{c} &=& \avg{m \vec{v}_\mrm{B}^\perp j^\perp (\vec{v}_\mrm{B})}_{\vec{v}_\mrm{AB}^\perp \lt 0} + \avg{m \vec{v'}_\mrm{B}^\perp j^\perp (\vec{v'}_\mrm{B})}_{\vec{v}_\mrm{AB}^\perp \lt 0} \label{eq:exs_flux} \\ &=& \frac{\rho}{2}\avg{m (\vec{v}_\mrm{B}^\perp)^2 + m (\vec{v}_\mrm{A}^\perp)^2} = \rho T \label{eq:exs_stress} \end{eqnarray}
|
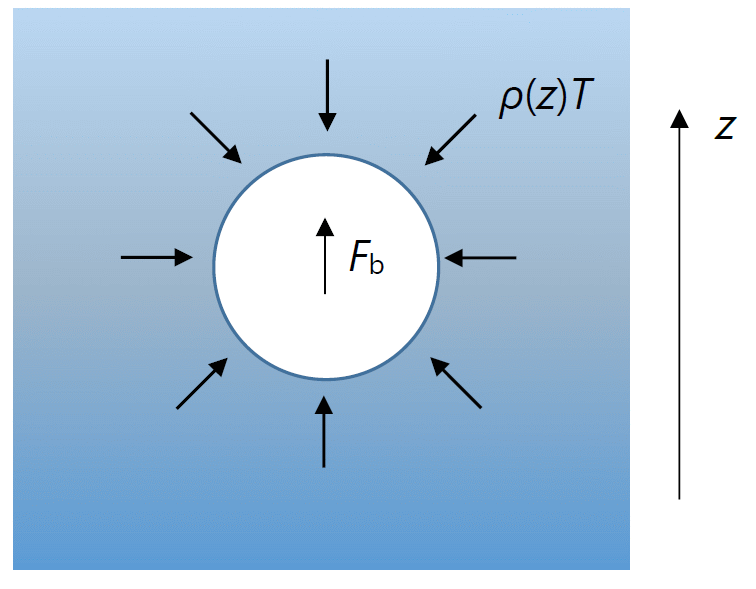
| 図 3-2. 希薄気体中の剛体球には、その排除球の表面に \(\rho T\) の圧力が働いていると考えられます。 密度勾配が存在する時、この球面に働く圧力を足しこんだものが浮力 \(F_\mrm{b}\) に相当します。 |
となり、気体の圧力と同じ \(\rho T\) の圧力(応力)が排除球の表面にかかる勘定になります。 剛体球にかかる力は、この圧力を排除球の表面について積分したものになり、 表面付近の密度 \(\rho\) が一定なら 0 になります。 けれども重力が働き、密度、圧力の勾配があれば、 液体中に沈めた物体同様、 浮力が働きます。
密度勾配が小さく、式 \eqref{eq:p_balance} の右辺で \(\rho(z) = \rho = \mbox{const}\) とすると、 通常の巨視的な物体の浮力同様、ガウス(・オストログラツキー)の定理から、 浮力 \(F_\mrm{b}\) は次式のように与えられます(圧力の向きに注意):
\begin{equation} F_\mrm{b} = -\int_S \vec{P} \cdot \vec{e} ~\rmd s = -\int_V \mrm{div} \vec{P} ~\rmd \vec{r} = -\int_V \frac{\rmd P(z)}{\rmd z} \rmd \vec{r} = m \rho g v_\mrm{ex} \label{eq:buoy_gasx} \end{equation}
ここで \(v_\mrm{ex}\) は排除球の体積、排除体積です。
\begin{equation} v_\mrm{ex} = \frac{4 \pi}{3} \sigma^3 \label{eq:exvol} \end{equation}
剛体球分子は排除球の体積(排除体積 \(v_\mrm{ex}\))分の流体を押しのけ、 その重さだけの浮力を感じることになります。 アルキメデスの原理は、剛体分子の体積として分子容(\(=1/\rho\))ではなく、 排除体積をとることで成立するわけです。
ある分子の上に乗って考える立場からは、重心運動と相対運動に分け、換算質量 \(m_\mrm{r} = m/2\) のパチンコ玉 B が、 静止したパチンコ玉 A に衝突してくると考える方が分かりやすいかもしれません。 この取り扱いでは、衝突パラメーターが \(\sigma\) より小さい場合について \[ p_\mrm{c} = 2\avg{m_\mrm{r} \vec{v}_\mrm{AB}^\perp j^\perp (\vec{v}_\mrm{AB})}_{\vec{v}_\mrm{AB}^\perp \lt 0} \] を評価することになり、 \[ \avg{(\vec{v}_\mrm{AB}^\perp)^2} = 2T/m = T/m_\mrm{r} \] であることに注意してやれば、同じく排除球表面に \(\rho T\) の圧力が働くことが分かります。 分子衝突の議論になじみがある人には、この方がいいかもしれません。
前節まで運動量の流れに注目して、剛体球流体の圧力と剛体球に働く力を眺めてみました。 分子が数密度 \(\rho\) で均一に分布しておれば、 流体には分子の並進運動に由来する \(\rho T\) の圧力が働きます。 またこの一方、分子間衝突(分子間相互作用)の結果、剛体球の排除球面上には \(\rho T\) の圧力が働いています。 ここでは、この両者が流体の圧力とどう関わるかについて考えてみます。
分子運動だけを考えれば、流体中のある平面を通して流れる運動量の流束は \(\rho T\) になります。 けれどもこの平面が剛体球分子の排除球をよぎる時、 その断面には分子が存在せず、分子が直接平面を通過して運搬する運動量はありませんが、 分子間力による運動量の流れが生じます。 つまり分子自体が運動量を運ぶのではなく、 分子間での運動量の受け渡しが起きるわけです。
|
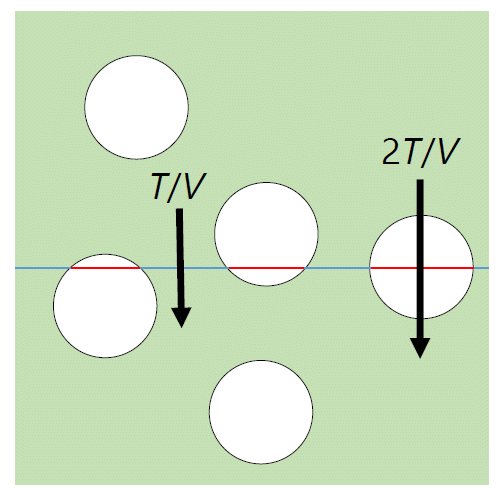
| 図 3-3. 体積 \(V\) の流体中に1個の剛体球を加えた時、 ある平面を通過する運動量の流束の変化を考えます(2次元的な概念図)。 他の剛体球が平面付近になければ、流束は \(T/V\) ですが、 平面が排除球をよぎる場合、分子衝突のため、その断面(図中の赤線)を通る流束は \(2T/V\) です。 |
前節の議論を振り返ってみると、 衝突にともなう運動量の移動が起きる時、 B の運動量が A に移動し、運動量の流れ、流束が生じ、それは平均すれば \(\rho T\) でした。 この時同様に A から B に運動量の流束が存在し、それも平均すれば \(\rho T\) のはずです。 つまり合計すれば、排除球を挟んで \(2\rho T\) の運動量の流束がある、 平面の排除球を切らない部分の 2 倍の運動量の流束、2倍の圧力が働いていることになっているわけです。 ですから平均してみれば、 排除球を切る面積に相当する分だけの圧力の増加が起きることになります。
分子間の衝突(相互作用)を扱うには、2個の分子の間の運動量のやり取りを同時に扱うことになるので少し厄介です。 そこである分子に乗って事態を眺め、 体積 \(V\) 一定の容器に 1 個の分子を挿入した時の圧力増加を考えてみましょう。 この分子の挿入を考える時、他の分子の配置は取りあえず固定して考えることにします。
分子衝突がない場合の圧力増加は、先に考えたのと同じで \(T/V\) です。 分子衝突が起きる場合、ここに \(T/V\) だけ圧力が嵩増しされます。 分子衝突が起きるのは考える平面が排除球を切断した断面で、 この切断面の分だけ、圧力増加が起きることになります。 この2種類の運動量の流束の内、分子自体が表面をよぎって流れる成分を「並進(運動)の圧力」\(p_\mrm{tr}\)、 分子衝突、分子間相互作用にともなう圧力への寄与を「分子間力による圧力」\(p_\mrm{mf}\) と呼ぶことにしましょう。 それぞれの寄与は次のように表すことができます:
\begin{eqnarray} p_\mrm{tr} &=& T/V \\ p_\mrm{mf} &=& \avg{s_\mrm{mf}} T/V \label{eq:p_col} \end{eqnarray}
|
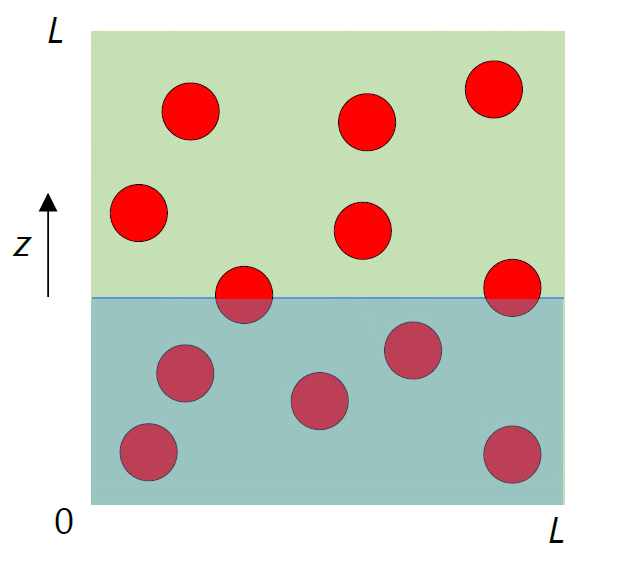
| 図 3-4. 分子間力による圧力を評価するため、 平面による排除球の切断面の面積を平均化して求めます(2次元化した概念図)。 密度が希薄なので排除球の重なりは無視でき、 積分値(式 \eqref{eq:cscal})は剛体球の配置に依存しません。 |
ここで \(s_\mrm{col}\) は、圧力を考える平面に占める、排除球の切断面の面積の割合です。 排除球の切断面の面積の割合の平均を求めるには、 図のように \(N\) 個の剛体球分子の入った1辺 \(L\) の立方体を考え、次式のように立方体の \(z\) 軸に垂直な平面について平均を取ればよいでしょう (数密度 \(\rho = N/L^3\))。 ここでは十分希薄だと考えているので、排除球の断面積の重なりは無視します(というか、重なりが無視できるぐらい希薄だと考えます)。
\begin{equation} \avg{s_\mrm{col}} = \frac{1}{L} \int_0^L s_\mrm{col}(z) \rmd z = \frac{1}{L} \int_0^L \frac{S_\mrm{col}(z)}{L^2} \rmd z = \frac{1}{L^3} N v_\mrm{ex} = \rho v_\mrm{ex} \label{eq:cscal} \end{equation}
ここで \(S_\mrm{col}(z)\) は、平面内の排除球の切断面の面積で、 それを \(z\) 軸方向に積分すれば、\(N\) 個の排除球の体積 \(Nv_\mrm{ex}\) になることを用いています。 なお排除球の断面積の重なりが無視できるぐらい希薄なので、 この値は剛体球分子の配置に依存しません。
こうして希薄な剛体球気体において、分子の挿入による圧力の増加は、 次式のように評価できることになります:
\begin{equation} \pdifA{P}{N}{V} = p_\mrm{tr} + p_\mrm{col} = (T/V) (1 + \rho v_\mrm{ex}) \label{eq:p_inc} \end{equation}
密度微分の形で書けば次式のようになり
\begin{equation} \pdif{P}{\rho} = V \pdifA{P}{N}{V} = T (1 + v_\mrm{ex} \rho) \label{eq:p_dif} \end{equation}
これを積分し、状態方程式をビリアル状態方程式の形で書くと次のようになります:
\begin{equation} \frac{P}{\rho T} = 1 + \frac{1}{2}v_\mrm{ex} \rho = 1 + B \rho \label{eq:p_2ndvir} \end{equation}
ここで \(B\) は第 2 ビリアル係数で、ファンデルワールス状態方程式の b パラメーターの議論でおなじみかもしれませんが、 排除体積の半分になります:
\begin{equation} B = \frac{2\pi}{3} \sigma^3 \label{eq:hs_2ndvir} \end{equation}
「分子間力による圧力」は、 ビリアル定理で言うところの内部ビリアルに対応します。 ここでの導出では簡明を期して、 体積一定の下での圧力の分子数依存性 \(\partial P/\partial N\) (~体積弾性率)を用いていますが、 密度が高くなり分子間の相関が大きくなってくると取り扱いが厄介になります。 むしろ前章で考えたような2成分混合系として扱った方が、 見通しは良く、ビリアル定理との対応もスムーズなようです。
等温圧縮率は、先の粒子数増加に対する圧力の応答の式 \eqref{eq:p_dif} からも明らかに、次式で与えられます。
\begin{equation} \kappa_T = \frac{1}{\rho} \pdif{\rho}{P} = \frac{1}{\rho T} \frac{1}{1 + 2B \rho} \approx \frac{1 - 2B \rho}{\rho T} \label{eq:comp_vir} \end{equation}
さて同様の筆法で、分子に働く浮力 \(F_\mrm{b}\) を考えてみましょう。 まず圧力の高度依存性について、先の圧力の釣り合いの式が成立しています:
\begin{equation} \frac{\rmd P(z)}{\rmd z} = -mg \rho(z) \label{eq:pbalancex} \end{equation}
この圧力の高度勾配を、先の「並進の圧力」と「分子間力による圧力」に分けて考えます。 分子間衝突による圧力が浮力 \(F_\mrm{b}\) を与えるので、圧力の高度依存性は次式のように書けます:
\begin{equation} \frac{\rmd P(z)}{\rmd z} = T\frac{\rmd \rho(z)}{\rmd z} - \rho(z) F_\mrm{b}(z) \label{eq:p_buoyx} \end{equation}
ここで分子間力による圧力の寄与は、浮力の反作用なので符号が逆で \(- \rho(z) F_\mrm{b}(z)\) になることに注意します。 また「並進の圧力」は、式 \eqref{eq:p_buoyx} の右辺第1項、密度勾配の項に相当するわけですが、 前章の扱いでいうと \(F^\circ_\mrm{X}(z)\) に照応します。
さて「並進の圧力」は等温圧縮率を用いて圧力勾配と関係づけられます:
\begin{equation} T\frac{\rmd \rho(z)}{\rmd z} = T \pdif{\rho(z)}{P(z)}\frac{\rmd P(z)}{\rmd z} = T \rho(z) \kappa_T(z) \frac{\rmd P(z)}{\rmd z} \label{eq:transpx} \end{equation}
この関係式を先の式 \eqref{eq:p_buoyx} に代入し、 式 \eqref{eq:pbalancex} を用いて、分子に働く浮力の表現を求めると次のようになります:
\begin{equation} \rho(z) F_\mrm{b}(z) = -[1- \rho(z) \kappa_T(z) T] \frac{\rmd P(z)}{\rmd z} = [1- \rho(z) \kappa_T(z) T] mg \rho(z) \label{eq:bforceq} \end{equation}
式 \eqref{eq:comp_vir} から \(1- \rho(z) \kappa_T(z) T\) は、\(2B\rho(z) = v_\mrm{ex}\rho(z)\) であり、 引数の \(z\) を省くと、 分子に働く浮力として次のように、 先の排除球に及ぼされる圧力から評価した式 \eqref{eq:buoy_gasx} と一致する結果を得ます。
\begin{equation} F_\mrm{b} = v_\mrm{ex} \rho mg \label{eq:bforcex} \end{equation}
前章の扱いと対応するように、 くどい導出を示しましたが、直接、ビリアル状態方程式 \eqref{eq:p_2ndvir} を用い、分子間力による圧力 \(B \rho^2 T\) の高度勾配から、分子に働く浮力を評価しても同じことになります (引数の \(z\) を省きます): \[ -\rho F_\mrm{b} = \frac{\rmd B \rho^2 T}{\rmd z} = 2B \rho T \frac{\rmd \rho}{\rmd z} \approx 2B \rho \frac{\rmd P}{\rmd z} = - v_\mrm{ex} \rho mg \rho \] \[ F_\mrm{b} = v_\mrm{ex} \rho mg \]