|
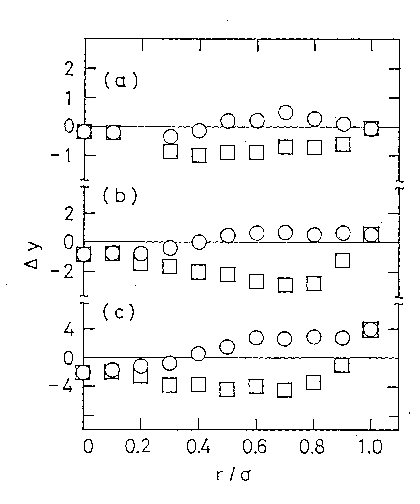
| 図 A5.1. \eqref{eq:A5.2} 式で見積られた空孔分布関数の計算機実験の結果[A5.3]からの偏差(○)。 図には Grundke-Henderson による見積もり[4.6]の偏差(□)も示してある。 (a) \(\eta = 0.3 (\pi/6)\)、(b) \(\eta = 0.5 (\pi/6)\)、(c) \(\eta = 0.7 (\pi/6)\) |
熱ようどう理論は主として、分子の動的な挙動とりわけブラウン運動に対して適用されてきた。 そのため必ずしも、今回問題にする熱力学的な問題についての熱ようどう理論の構成は知られていないように思われる。 一般論は成書[A1.1]にゆずりここでは、その概要を本研究と関連する粒子数のゆらぎに即して述べておくことにする。
ある注目する部分系 Y、そしてそれと接する熱浴としてまた粒子の供給、受容を行なう粒子浴としても機能する系 X とからなる系を考える。 ここで圧力による内部エネルギ-の変化を考慮しなくてもよいように X、Y はいずれも体積が一定に保たれているとする。 また熱浴 X のエントロピ-は粒子の出入りによっては変化しないと考え、また逆に熱の出入りによって粒子数は変化しないする。 これは、X がよく制御されていること、つまりよい観測器として働くことを示す。 われわれは、Y という部分系に対し、ここで考えた X という系のようにふるまっているわけである。
それぞれの系を特徴付ける変数の組を \(\alpha^\mrm{Y}\)、\(\alpha^\mrm{X}\) とし、 これらは熱平衡における値 \(\alpha^\mrm{Y}_0\)、\(\alpha^\mrm{X}_0\) から \(\delta \alpha^\mrm{Y}\)、\(\delta \alpha^\mrm{X}\) だけゆらいでいるものとしよう。 ここで \(\alpha\) は具体的には内部エネルギ-、エントロピ-と粒子数である。 今系が \(\alpha^\mrm{Y}_0 + \delta \alpha^\mrm{Y}\)、 \(\alpha^\mrm{X}_0 + \delta \alpha^\mrm{X}\) という状態にある確率 \(W(\delta \alpha^\mrm{Y}, \delta \alpha^\mrm{X})\) を考える。 熱平衡状態 \((\alpha^\mrm{Y}_0, \alpha^\mrm{X}_0)\) は、この確率を最大にする状態ということになる。 ここで、この確率分布 \(W(\delta \alpha^\mrm{Y}, \delta \alpha^\mrm{X})\)を全系のエントロピ- \(S(\delta \alpha^\mrm{Y}, \delta \alpha^\mrm{X})\)を用いて
\begin{equation} W(\delta \alpha^\mrm{Y}, \delta \alpha^\mrm{X}) = A \exp[ S(\delta \alpha^\mrm{Y}, \delta \alpha^\mrm{X})/k_\mrm{B}] \label{eq:A1.1} \end{equation}
と書けると仮定する。 この確率とエントロピ-を結びつけた表式は、熱平衡でエントロピ-が最大となることにちょうど対応する。 したがって、熱平衡状態の周りにおけるエントロピ-という熱力学量の挙動を調べることによって、系の熱平衡状態でのゆらぎという確率論的な情報を得ることができることになる。 したがって問題は熱平衡の近傍での熱力学諸量の微小な変化にともなうエントロピ-変化の表式を得ることに帰着する。 これは、次のようにして得ることができる。(以下 X、Y の体積は一定に保たれていることに注意されたい)
部分系 Y に対して熱力学第一法則から次の関係が成立する。
\begin{equation} \delta U^\mrm{Y} = Q + \sum_i \mu_i^\mrm{X} \delta N_i^\mrm{Y} \label{eq:A1.2} \end{equation}
全系のエントロピ-変化を考えると
\begin{eqnarray} \delta S &=& \delta S^\mrm{X} + \delta S^\mrm{Y} \nonumber \\ &=& -Q/T^\mrm{X} + \delta S^\mrm{Y} \label{eq:A1.3} \end{eqnarray}
\eqref{eq:A1.3} 式に\eqref{eq:A1.2} 式を代入して
\begin{equation} \delta S = -(\delta U^\mrm{Y} - \sum_i \mu_i^\mrm{X} \delta N_i^\mrm{Y} - T^\mrm{X} \delta S^\mrm{Y})/T^\mrm{X} \label{eq:A1.4} \end{equation}
を得ることができる。 確率分布 \(W(\delta \alpha^\mrm{Y}, \delta \alpha^\mrm{X})\) はXに関わる熱力学的変数のゆらぎも含んでいるわけだが、 \eqref{eq:A1.4} 式にみるように考慮する必要がなくなる。 そこで 、 \eqref{eq:A1.1} 式に\eqref{eq:A1.4} 式を代入し \(\delta \alpha^\mrm{X}\) について積分し
\begin{equation} W(\delta \alpha^\mrm{Y}) = W_0 \exp \left[ -\frac{\delta U^\mrm{Y} - \sum_i \mu_i^\mrm{X} \delta N_i^\mrm{Y} - T^\mrm{X} \delta S^\mrm{Y})}{k_\mrm{B} T^\mrm{X}} \right] \label{eq:A1.5} \end{equation}
式を得る。
一般に熱平衡では \(W\) は極値をとっており \eqref{eq:A1.5} 式の指数部の内容は一次の変分については0である。 したがって、静的にある状態をとらえるためには二次の変分をとる必要が生まれる。 しかし、ただ系がゆらいでいる、それだけでは何らわれわれの関心をひくものではない。 われわれが、観測する、そのことによって観測にかかるものこそが意味を持つ。 したがって、問題とすべきはこの確率分布がわれわれの観測(すなわち X の側の温度・圧力を変化させること)に対していかに応答するかでなければならない。 このとき、ちょうど量子力学で波動関数それ自身は観測にかかるものでないように確率分布そのものが観測にかかるわけではない。 われわれの観測する Y の性質(ここでは粒子数ということになる)の期待値の応答という形でわれわれはこの確率分布の応答を見ることになる。 ここで問題にする粒子数の期待値 \(\langle N_j^\mrm{Y} \rangle\) の化学ポテンシャル変化 \(\mu_i^\mrm{X}\) に対する応答関数は
\begin{equation} \mbox{応答関数}~= \pdif{\langle N_j^\mrm{Y} \rangle}{\mu_i^\mrm{X}} \label{eq:A1.6} \end{equation}
のように定義できる。 ここで \(\langle N^\mrm{Y} \rangle\) は次のように表わされる。
\begin{equation} \langle N^\mrm{Y} \rangle = \int (N_{0}^\mrm{Y} + \delta N^\mrm{Y}) W(\delta \alpha^\mrm{Y}) \rmd (\delta \alpha^\mrm{Y}) \label{eq:A1.7} \end{equation}
したがって、\eqref{eq:A1.7} 式を \eqref{eq:A1.6} 式に代入して
\begin{equation} \pdif{\langle N_j^\mrm{Y} \rangle}{\mu_i^\mrm{X}} = \pdif{\langle N_i^\mrm{Y} \rangle}{\mu_j^\mrm{X}} = \frac{\langle \delta N_i^\mrm{Y} \delta N_j^\mrm{Y} \rangle}{k_\mrm{B} T} \label{eq:A1.8} \end{equation}
をえる。 ここで、\(\langle \delta N^\mrm{Y} \rangle = 0\) となることを用いた。 本研究でしばしば問題とする粒子数ゆらぎはこのように、粒子数の化学ポテンシャルに対する応答として観測にかかる量なのである。
上で、粒子数ゆらぎについての表式を与えた。 ここで \(i, j\) の密度が十分低い場合、溶液でいえば無限希釈状態での粒子数ゆらぎを考えてみよう。 \(i \ne j\) の時には両者の間には相関がないはずで、\eqref{eq:A1.8} 式は0である。 \(i = j\) の時には
\begin{eqnarray} \pdif{\langle N_i^\mrm{Y} \rangle}{\mu_i^\mrm{X}} &=& \frac{\langle (\delta N_i^\mrm{Y})^2 \rangle}{k_\mrm{B} T} \nonumber \\ &=& \frac{\langle N_i^\mrm{Y} \rangle}{k_\mrm{B} T} \label{eq:A1.9} \end{eqnarray}
が成立する。 これは、次のような確率論的考察からえることができる。 多数の箱(\(N\)個あるとする)を考えここに \(i\) 種の粒子を 1 個ずつ \(IN\) 個投入していくとする。 このとき一回の試行ごとにある箱の中に入る確率は \(1/N\) である。 (\(i\) 種の粒子の間には相関がないと考えているのでそれぞれの試行は独立である) こうしてえられる粒子数分布は二項分布に従いその期待値は
\begin{equation} IN \x (1/N) = I \label{eq:A1.10} \end{equation}
であり、その分散、ゆらぎは
\begin{equation} I N \x (1/N) (1 - 1/N) = I (1-1/N) \label{eq:A1.11} \end{equation}
である。 \(N\) が十分大きければゆらぎの大きさは \(I\)、すなわち粒子数の期待値に一致する。 つまり、\eqref{eq:A1.9} 式がえられたわけである。
Kirkwood と Buff は1951年多成分系のゆらぎを論じ、部分分子容に対するゆらぎからの表現を与えた[A2.1]。 原論文におけるその導出はいささか回りくどいものなので、ここではもっと直接的な導出を行なうことにする。
1 章で見た部分分子容の表式は、われわれが容易に実現しうる条件におけるものである(\(T\),\(P\) および粒子数を一定に保つのは比較的容易)。 これを熱ようどう理論における表式に近づけるためには、示強的変数を一定にした条件、つまり粒子数一定の条件を、化学ポテンシャル一定の条件にひきなおさねばならない。 ヤコビアンによる表現を用いて、それは以下のように行なうことができる。
\begin{eqnarray} \bar{V}_j\ &=& \pdif{(T,P, V, N_{i \ne j})}{(T,P, N_{i})} \nonumber \\ &=& \pdif{(T, V, N_i)}{(T, P, N_i)} \pdif{(T,P, V, N_{i \ne j})}{(T,V, \mu_{i})} / \pdif{(T, V, N_i)}{(T,V, \mu_{i})} \nonumber \\ &=& \kappa_T \sum_i (N_i A_{ij}^{-1}) \label{eq:A2.1} \end{eqnarray}
ここで、\(\mu\) は化学ポテンシャル、\(\kappa_T\) は等温圧縮率、\(A\) は、その \((i,j)\) 成分 \(A_{ij}\) が
\begin{equation} A_{ij} = \pdif{N_i}{\mu_j} = \pdif{N_j}{\mu_i} \end{equation}
である行列であり \(A^{-1}\) はその逆行列である。 \(A\) のそれぞれの成分は、体積を固定したときの粒子数ゆらぎに相当する。(付録1を見よ)
\eqref{eq:A2.1} 式の表現から、部分分子容は圧縮率を通して、注目する分子種についての粒子数ゆらぎと密接な関係にあることがわかる。 さらに、圧縮率は次のように全体系の粒子数ゆらぎと関係付けられている。
\begin{eqnarray} -V \kappa_T &=& \pdif{(T, V, N_i)}{(T,P, N_{i})} \nonumber \\ &=& \pdif{(T, V, N_i)}{(T, V, \mu_i)} / \pdif{(T,P, N_i)}{(T,V, \mu_i)} \nonumber \\ &=& - (\tilde{\vec{n}} A^{-1} \vec{n})^{-1} \label{eq:A2.2} \end{eqnarray}
ここで、\(\vec{n}\) はその \(i\) 行目が \(i\) 成分の濃度 \(N_i / V\) である列ベクトルであり、~ はそれを転置したものを示す。 したがって、部分分子容について最終的な表式として次式をえる。
\begin{equation} \vec{\bar{V}} = \frac{A^{-1} \vec{n}}{\tilde{\vec{n}} A^{-1} \vec{n}} \label{eq:A2.3} \end{equation}
ここで、\(\vec{\bar{V}}\) はその \(i\) 行目が \(i\) 成分の部分分子容である列ベクトルである。 爾来、分子の配置のみによって部分分子容が決まるといわれてきたが、その具体的な形がここにある。
本研究ではすべて、古典的な体系としての取扱いを行なうわけだが、粒子間に強い相互作用が働く場合には量子化の効果を無視することができなくなる。 極端な場合をいえば、2個の粒子が強い相互作用の結果まったく同じ並進運動を行なう(2個の粒子が融合する)場合には、 部分分子容に対する並進の寄与は半減する( \(\kappa_T k_\mrm{B} T\) だけ減少する)。 化学反応でこのような問題を扱う際には今回のように頭から粒子数の変化として扱うが、粒子数は変化していないとする扱いもありうる。 後者の立場から問題を処理するには量子化の問題はさけられない。 ここでは流体における量子効果の度合を論じ、それが普通われわれが取扱うような流体においては十分無視できる程度のものであることを示す。
一般に状態和は、プランク定数の2乗 \(\hbar^2\) の巾で展開することができる。 並進運動をあつかう際には展開して
\begin{equation} \frac{Z}{Z_\mrm{cl}} = 1 - \frac{\hbar^2 \langle F^2 \rangle}{ 24 (k_\mrm{B} T)^2 m} \label{eq:A3.1} \end{equation}
がえられる [A1.1a]。 ここで \(Z\) は体系の状態和、\(Z_\mrm{cl}\) はそれに対する古典近似、\(F\) は考える粒子に働く力そして \(m\) はその粒子の質量である。 このような表式だけではどの程度の量子補正が現われるものか明らかでないので、実際にこの量子補正の項の大きさを見積ってみることにしよう。
代表的な値として \(m = \mrm{2 \x 10^{-25}~ kg}\) (分子量 120), \(T = 300~\mrm{K}\) を用いれば
\begin{equation} Z/Z_\mrm{cl} = 1 - (3.3 \x 10^{16} \mrm{~N^{-2}}) \langle F^2 \rangle \label{eq:A3.2} \end{equation}
したがって、1個の分子にかかる力の期待値が ~10-9 N よりも大きくなれば量子補正が重要となる。 液体について単純な概算を行なってみよう。 液体中で一辺の長さ \(\sigma\) が分子のサイズ程度の小さな立方体を考えよう。 互いに向き合う面にかかる圧力を \(P_1, P_1', \cdots, P_3, P_3'\) とすれば
\begin{equation} \langle F^2 \rangle/\sigma^4 \sim \sum \langle (P_i - P_i')^2 \rangle \label{eq:A3.3} \end{equation}
ここで等方的に力がかかるとし、さらに各面に働く圧力のゆらぎ \(\delta P \) はそれぞれ独立であるとすると \eqref{eq:A3.3} 式は次のようになる。
\begin{equation} \langle F^2 \rangle/\sigma^4 \sim 6 \langle (\delta P)^2 \rangle \label{eq:A3.4} \end{equation}
ここで、圧力のゆらぎを十分大きな体系についての表現
\begin{equation} \langle (\delta P)^2 \rangle = k_\mrm{B} T / (V \kappa_S) \label{eq:A3.5} \end{equation}
で見積る。ここ \(\kappa_S\) は断熱圧縮率である。 \(V = \sigma^3\) であり \eqref{eq:A3.4} 式から粒子に働く力のゆらぎは
\begin{equation} \langle F^2 \rangle \sim 6 k_\mrm{B} T \sigma / \kappa_S \label{eq:A3.6} \end{equation}
となる。ここで、\(\sigma = 0.5~\mrm{nm}\)、\(\kappa_S = 1 \x 10^{-9}~\mrm{ Pa^{-1}}\) とすれば
\begin{equation} \langle F^2 \rangle \sim 1.2 \x 10^{-20}~\mrm{N^2} \label{eq:A3.7} \end{equation}
という結果をえる。 したがって、普通考える液体については \eqref{eq:A3.2} 式によって古典的な状態和は 10-4 のオ-ダ-まで妥当であることがわかる。
希薄気体中における厳密な結果として、4.2b 節の \(\delta V\) についての結果と、 \(v(\mrm{配置})\) が \((\pi/6)(\sigma + \sigma_\mrm{S})^3\) であることを用いて \(\alpha\) と \(\beta\) をえることができる。 ここでは、 \(\alpha\) と \(\beta\) という視点ではなく5章での分子各部のパッキングという観点から、希薄気体中の部分分子容を考えてみることにする。
5.5 節によれば、シリンダ-部分、半球部分のコアの体積の部分分子容への寄与の度合 \(a_1\)、\(a_2\) は
\begin{equation} a_1 = [v + \Delta v]/[\mbox{単位シリンダ-のコアの体積}] \label{eq:A4.1} \end{equation}
\begin{equation} a_2 = [v(\mbox{配置})]/[\mbox{半球部分ののコアの体積}] \label{eq:A4.2} \end{equation}
である。 したがって、6章でのモデルにおける単位シリンダ-のコアの体積としてメチレン基に相当するコアの体積をとって、\(a_1\)、\(a_2\) を求めることができる。 具体的に書けば \(d \lt \sigma\) の場合について
\begin{equation} a_1 = \frac{(\pi/4) (\sigma + \sigma_\mrm{S})^2 L - (\pi/12) L^3}{(\pi/4) \sigma^2 L - (\pi/12) L^3} \label{eq:A4.3} \end{equation}
\begin{equation} a_2 = \frac{(\pi/6) (\sigma + \sigma_\mrm{S})^3}{(\pi/6) \sigma^3} \label{eq:A4.4} \end{equation}
整理して
\begin{equation} a_1 = \frac{3 (1 + s)^2 - (L/\sigma)^2}{3 - (L/\sigma)^2} \label{eq:A4.5} \end{equation}
\begin{equation} a_2 = (1 + s)^3 \label{eq:A4.6} \end{equation}
ここで \(s = \sigma_\mrm{S}/\sigma\) とおいた。 この両者の大きさを比較するためこの差をとると
\begin{equation} a_2 - a_1 = \frac{s^2 (2s + 3) + [1 - (L/\sigma)^2] [(1+s)^3 -1]}{3 - (L/\sigma)^2} \label{eq:A4.7} \end{equation}
ここで \(L/\sigma \lt 1\) であるから、\(a_2\) の方が \(a_1\) よりも大きい。 つまり、半球部分の方がシリンダ-部分に比べてパッキングのされ方が悪いという5章での結果がこの希薄気体における取り扱いでも示されたわけである。 ここでは、剛体球の集まりとしてアルカン分子のコアを記述することによってこの結果を得たわけだが、5章で用いたアルカン分子のコアによっても同様にこれを示すことができる。
\eqref{eq:A4.5} および \eqref{eq:A4.6} 式からは、溶媒のサイズよるパッキングのようすの変化も評価することができる。 \(L, \sigma\) を一定にしておけば、溶媒のサイズ \(\sigma_\mrm{S}\) が大きくなるにしたがい \(a_2\) の方は \(\sigma_\mrm{S}\) の3次関数にしたがい増大するのに対して、 \(a_1\) の方は \(\sigma_\mrm{S}\) の2乗に依存する。 つまり、半球部分の方が溶媒のサイズについてより敏感なのである。 たとえば、\(L/\sigma\) を 0.4 としたとき \(s = \sigma_\mrm{S}/\sigma\) を 0、0.5、1 と大きくしていくと \(a_1\) は 1、2.32、4.17 となるのに対し、 \(a_2\) は 1、3.38、8 となる。 なお普通の溶媒について \(s\) の値は少なくとも 1 以上であるはずで、これらの \(a_1\) 、\(a_2\) の値は5章でみたものよりはるかに大きく、また溶媒に対してはるかに敏感である。 これは多体的な相互作用がここには入っていないためで、それについては本文を見られたい。
空孔分布関数をどのように解析的な形で見積るかについてはまだ決定的といえるものは与えられていないようである。 ここでは、Grundke-Henderson(G-H) による方法 [4.6](これに少し手を加えたものに Pratt らによるもの [A5.1]がある)を基礎に空孔分布関数の解析的な形を与える。 ここでは、問題にする相関の距離が剛体球の直径\(\sigma\)よりも短いところを取り扱う。剛体球からなる系でこの領域は単調な変化をすることが知られている。
Percus-Yevick 方程式からの動径分布関数の解からは空孔分布関数として
\begin{equation} y(r) = c_0 + c_1 r + c_3 r^3 \label{eq:A5.1} \end{equation}
で与えられる。ここでは、これと似た形で
\begin{equation} \ln y(r) = a_0 + a_1 (r/\sigma) + a_3 (r/\sigma)^3 \label{eq:A5.2} \end{equation}
という関数形で空孔分布関数を近似することを考える。 この式は \eqref{eq:A5.1} 式と \(\eta \to 0\) の極限で一致する。 この式はまた 4.2b 節で見たように剛体球同士が重なるときの体積変化の表現には \(r\) について2次の項が現われないことに対応している。 (\eqref{eq:A5.2} 式の圧力微分が配置の体積変化に対応することに注意されたい)
このように空孔分布関数の形が決まればその係数を次の関係から定めることができる。
ここで上付き CS は 4.4a 節(4.4.1)式にある Carnahan-Starling 式を示す。 \(\mu^\mrm{E}\) は過剰の化学ポテンシャル、つまり溶媒との相互作用がない場合の化学ポテンシャルと実際の化学ポテンシャルとの差、 5.6 節における \(W\) に相当する。 ここで、\eqref{eq:A5.3-4} 式は"0距離定理"と呼ばれるものである[A5.2]。 この過剰の化学ポテンシャルは Carnahan-Starling の式からえられる溶液の \(PVT\) 挙動から容易に算出することができる。 この、3 個の条件から定まった係数 \(a_0\)、\(a_1\)、\(a_3\) はあからさまな形では次のようになる。
\begin{equation} a_0 = (-1 + 3s^2 - 2s^3) \ln (1 - \eta) + \frac{3 \eta}{1 - \eta} s + \frac{3 \eta (2-\eta)}{(1-\eta)^2} s^2 + \frac{\eta (1-6 \eta + 3 \eta^2)}{(1-\eta)^3} s^3 \label{eq:A5.6} \end{equation}
\begin{equation} a_1 = -\frac{3}{2} s (1+s)^2 \eta \left[ \frac{1}{1 - \eta} + \frac{3 s}{1 + s} \frac{\eta}{(1-\eta)^2} + 2 \left(\frac{s}{1+s} \right)^2 \frac{\eta^2}{(1-\eta)^3} \right] \label{eq:A5.7} \end{equation}
\begin{equation} a_3 = \ln \left[ \frac{1}{1-\eta} + \frac{3}{2} s \frac{\eta}{1-\eta} +\frac{s^2}{2} \frac{\eta^2}{(1-\eta)^3} \right] - a_0 - a_1 \label{eq:A5.8} \end{equation}

|
| 図 A5.1. \eqref{eq:A5.2} 式で見積られた空孔分布関数の計算機実験の結果[A5.3]からの偏差(○)。 図には Grundke-Henderson による見積もり[4.6]の偏差(□)も示してある。 (a) \(\eta = 0.3 (\pi/6)\)、(b) \(\eta = 0.5 (\pi/6)\)、(c) \(\eta = 0.7 (\pi/6)\) |
今回得られた結果と、モンテカルロ法を用いた計算機実験(\(\sigma = \sigma_\mrm{S}\))の結果[A5.3]との一致はきわめて良好である。 モンテカルロ計算の結果からの \eqref{eq:A5.2} 式のはずれを
\begin{equation} \Delta y = 100 [y^\mrm{A5}(r) - y^\mrm{MC}(r)]/y^\mrm{MC}(r) \label{eq:A5.9} \end{equation}
でもって評価して図に示した。 ここで上付き A5 はここでの見積もりの結果を、MC はモンテカルロ計算の結果を表わしている。 密度が高くなると偏差は大きくなる傾向にある。 しかし \(r = \sigma\) の点におけるはずれがその中でも大きく現われているように、これは係数の評価に用いた Carnahan-Starling 式の偏差に起因しているように思われ、 \eqref{eq:A5.2} 式の関数形自身は十分なもののように思われる。
最初に触れた G-H による見積もりからの結果を同じく図に示しておく。 G-H によるものは今回のものよりも項の数は多く(\(r\) について2次の項を含む)、より一致はよくなるものと期待されるが、皮肉なことに簡単な今回の式よりも一致はよくない。 これはおそらく、かれらが \eqref{eq:A5.8}式に加えて用いた接触距離における \(y(r)\) の傾きの評価に問題があったためと思われる。