1．呼気の赤外吸収スペクトル測定

呼気の赤外吸収スペクトルのこと

ここではまず、 最も身近な気体といえる呼気の赤外吸収スペクトルを測り、 地球温暖化と関わってよく話題に上る二酸化炭素に注目して、 気体の赤外スペクトルを眺めてもらうことに主眼をおいています。 そもそもどんなスペクトルが得られ、 それがどんな風に解釈できるのか、 教科書で習うことを念頭に、 いろいろ考えてもらえればよいでしょう。

呼気の赤外吸収スペクトルの測定

測定にあたっては、これまで有機化学実験でおなじみの ATR 装置のユニットを、 透過測定のユニットに付け替えます。 気体を容器に閉じ込めておかないと拡散して測れなくなってしまうわけですが、 ここでは拡散してなくならないうちに測ってしまうという戦略を取ります。 これは呼気のように、毒性や腐食性がなく大量に供給可能な気体サンプルについては有効な手法になります。 検討課題にあるように都市ガス、 あるいはエアダスター（用意してあるのはジメチルエーテルを使ったもの）を測ったりしてもらってよいでしょう。

図1a. 有機化学実験でおなじみの ATR 法の測定ユニット。 今回は主役ではありません。	図1b. 透過型のユニットに付け替え、 ここに呼気を吹き込む。 二酸化炭素濃度が高すぎて測定値が振り切れたら、 適当に扇いで濃度を下げる。

呼気と二酸化炭素の赤外吸収スペクトル

実際にどんなスペクトルがえられるのか、 まずはお示ししましょう。 息を吹き込み過ぎると 2300 cm^-1 ぐらいのピークが振り切れたりしますが、 そこは適当に団扇であおいだりして、吸光度がだいたい 1 以内になるように収めるようにしましょう。

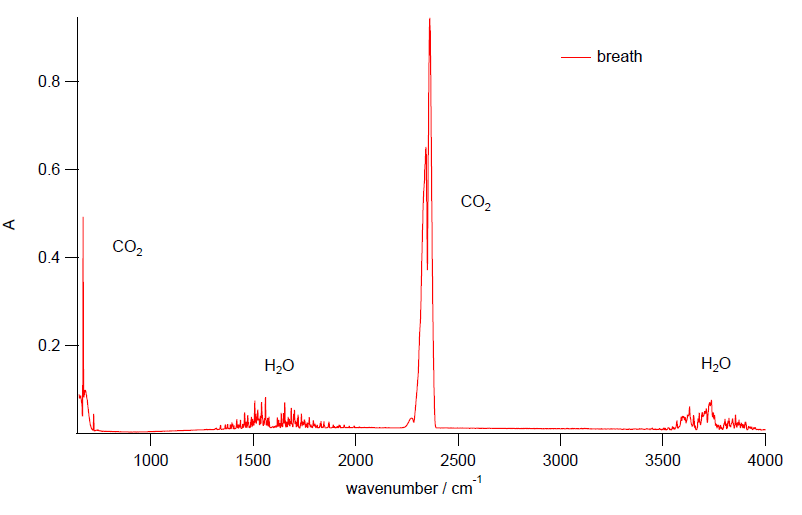
図2. 呼気の赤外吸収スペクトル。 テキストの解説、分子の基準振動の数値を参考に、 吸収を二酸化炭素と水に帰属。 「教科書的」にはこれでいいのだが・・・

課題にもありますが、 呼気の中で赤外吸収を示すと期待されるのは、 二酸化炭素 CO₂ と水 H₂O です （CO₂ は、 平衡位置では極性（双極子モーメント）がありませんが、 振動することで極性を獲得できることに注意）。 テキストの解説、分子の基準振動をみると、

二酸化炭素 CO₂ には、 対称伸縮振動：1340 cm^-1、 変角振動：666 cm^-1、 逆対称伸縮振動：2350 cm^-1

水 H₂O には 対称伸縮振動：3652 cm^-1、 変角振動：1596 cm^-1、 逆対称伸縮振動：3756 cm^-1

があると書いてあります。 そして課題の２番目にもありますが、 二酸化炭素の対称伸縮振動（1340 cm^-1）は、振動しても極性が現れないので、 赤外線は吸収しないでしょう。 測定される赤外吸収スペクトルには、 それぞれ不思議な形状の吸収帯が大きく４カ所にあり、 この基準振動数を割り振ってみると、図2 のように

700 cm^-1 付近は CO₂ の変角振動
1500 cm^-1 付近は H₂O の変角振動
2300 cm^-1 付近は CO₂ の逆対称伸縮振動
3500 cm^-1 付近は H₂O の伸縮振動（対称・逆対称）

と割り振られ、 それぞれに回転運動にともなう、 奇妙な構造が付いているという風に考えられます。

回転スペクトルのかたち

回転運動にともなうスペクトルの構造を二酸化炭素 CO₂ について簡単に見てみましょう （H₂O の回転運動は複雑でここでは取り上げません）。 図 3 に対応する領域のスペクトルを拡大して示しました。 700 cm^-1 付近の変角振動の吸収では中央に鋭いピークがあり、 その両脇になだらかな吸収帯が伸びています。 この吸収帯の左右のなだらかな吸収帯を P 枝（P branch）、R 枝、 中央の鋭いピークを Q 枝と呼んでいます。 一方 2300 cm^-1 付近の逆対称伸縮振動では、 中央のピーク、Q 枝がなく、両脇の吸収帯 P 枝と R 枝が見られます。

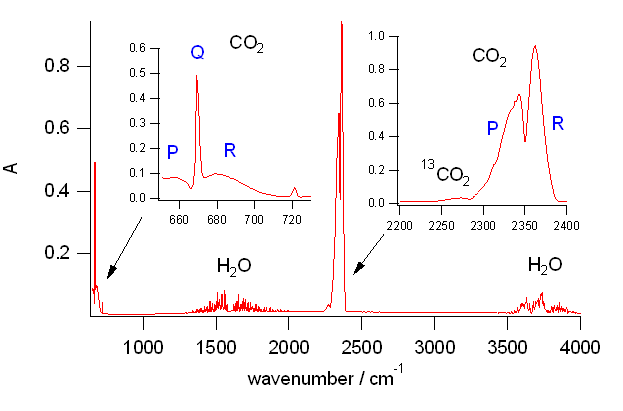
図3. 二酸化炭素の変角振動と逆対称伸縮振動のスペクトルの構造。 変角振動（700 cm^-1 付近）では中央にスパイクがあり、 逆対称伸縮振動（2300 cm^-1 付近）は中央が凹んでいる。 逆対称伸縮振動の吸収が大きいので、 ¹³C 由来の吸収ピークも検出可能。

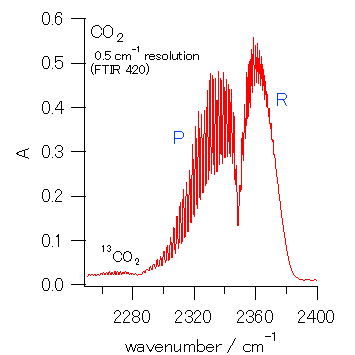
図4. スペックの高い FTIR 装置で分解能を上げて取った、 CO₂ の逆対称伸縮振動の吸収。

このように振動数が低くなる側（P 枝）、 高くなる側（R 枝）に吸収帯が伸びているのですが、 これをさる研究室で使っていたスペックの高い FT-IR 装置を用い、 分解能を上げて取った結果を図 4 に示します。 図 3 でも少しガタガタした様子がうかがえましたが、 それぞれの吸収帯は多数の吸収線から構成されています。 このような構造が生まれるのは、 回転運動が振動運動同様に量子化されている結果で、 その詳細はもっと回転線の構造が観察しやすい塩化水素について検討してもらうことになります。

課題にもありますが、 無論、振動数が低くなる側（P 枝）は回転エネルギーが減る吸収、 高くなる側（R 枝）に回転エネルギーが増える吸収です。 減る以上は最初分子が回転エネルギーを持っていたわけですが、 それは「熱エネルギー」として持っていたはずです。 熱エネルギー \(k_\mrm{B} T\) は先にエネルギーの換算で見たように、 1 K がおよそ 0.7 cm^-1 に対応しますから、 室温付近なら 200 cm^-1 程度です。 この巾程度の中のエネルギー遷移ですから、 P 枝がこの巾に収まっているのはまあ納得できるでしょう。 ではエネルギーの増える R 枝は青天井で、どんどん広がっていくのか？ ここは振動スペクトル同様、 量子数が 2 以上変化するような吸収が出てこないという制約が働いています （無論この制約は P 枝についても働いている）。

振動数が低くなる側（P 枝）の方が、 高くなる側（R 枝）に比べて吸収が弱いというのは、 詳細に議論し始めると難しい問題を含んでいます。 けれども大雑把にいうと、 エネルギーを投入して加熱するわけですから、 高温の状態が実現する方向、 より回転エネルギーの大きくなる吸収が強くなるのは期待してよいでしょう。

ここでは吸収の強い逆対称伸縮振動に注目しましたが、 変角振動（700 cm^-1 付近）の P 枝と R 枝についても同様の観察が成り立ちます。 ただし変角振動では、鋭いピーク、Q 枝がありました。 Q 枝は回転エネルギーが変化しない吸収に対応します。 逆対称伸縮振動で Q 枝が現れないのは、 回転軸と振動の方向が直交していることに由来しますが、 ちょっと議論は複雑になります。 また Q 枝のピークは P 枝と R 枝の中央ではなく、 R 枝の方に偏っています。 これはなぜでしょう？ これはさらに厄介な問題に発展していきます （CO₂ の基底状態では回転量子数は偶数）。 また P 枝に比べて R 枝は痩せています （全体の幅が狭く、ギザギザの幅も狭い）。 これはなぜでしょう？ といった具合に、 スルメを噛むように話がどんどん広がっていきます。 こうした話に ”共鳴” できる人は「分子分光学」のオタクになる資格十分です。 ぼくにはとても無理ですが・・・

同位体の存在

先にも指摘したように、 課題にある ¹³CO₂ 由来の吸収は、 図 3 や図 4 に示したように、 強い逆対称伸縮振動の少し低波数側にかすかに見えています。 補足の解説の式にあるように、 直線 X-Y-X 型分子の逆対称伸縮振動の角振動数 \(\omega_\mrm{asym}\)は、 ばね定数を \(k\) として次式で与えられます。

\begin{equation} \omega_\mrm{asym} = \sqrt{k (m_\mrm{Y} + 2m_\mrm{X})/m_\mrm{X} m_\mrm{Y}} \label{eq:XYXasym} \end{equation}

ですからばね定数が同じなら、 ¹³CO₂ と ¹²CO₂ の振動数の比は

\begin{equation} \frac{\omega_\mrm{asym}({}^{13} \mrm{CO_2})}{\omega_\mrm{asym}({}^{12} \mrm{CO_2})} = \sqrt{ \frac{m_\mrm{{}^{13} C} + 2m_\mrm{O}}{m_\mrm{O} m_\mrm{{}^{13} C}} \frac{m_\mrm{O} m_\mrm{{}^{12} C}}{m_\mrm{{}^{12} C} + 2m_\mrm{O}} } = \sqrt{\frac{13 + 2 \times 16}{13}\frac{12}{12 + 2 \times 16}} = 0.972 \label{eq:c13ratio} \end{equation}

逆対称伸縮振動の吸収には 2350 cm^-1 に吸収のくぼみがありますから、 ¹³CO₂ 由来の吸収のくぼみは 2350 cm^-1 × 0.972 = 2283 cm^-1 に出ることが期待され、 実際、低波数側のくぼみは 2283 cm^-1 にあるので、 計算通りです （¹³CO₂ の R 枝は¹²CO₂ の P 枝に隠れて見えない）。

この¹³CO₂ の吸光度から、 ¹³C の存在比を大雑把に評価すると、 5 %ぐらいになるでしょうか。 天然存在比として知られている 1.1 %よりかなり大きくなりますが、 これは背景にある¹²CO₂の P 枝の寄与を差し引く必要があるためで、 測定の際に差し引くバックグラウンドの問題もあって、存在比を精確に求めるのは困難です。

なお同位体としては酸素の同位体¹⁸O を持つ CO¹⁸O も興味あるところです。 ¹⁸O-C -O 分子については、対称伸縮振動なので見えなかった 1600 cm^-1 付近の振動も見えるはずです。 けれども天然存在比が 0.2 % と¹³C のさらに 1/5 で、 ちょっと Cary 630 で観測することは無理なようです。

温室効果との関り

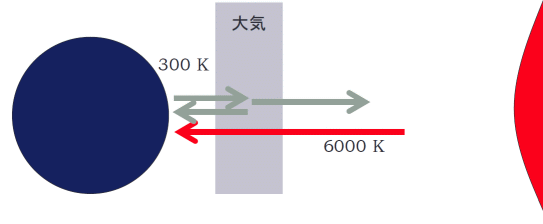
図5. 温室効果の概念図。 地球は太陽からのおよそ 6000 K の輻射を受け取って、 300 K 程度の輻射を放つ。 大気の 300 K の輻射の吸収・放射が増加すると、 宇宙空間への輻射が妨げられ地球は温暖化する。

二酸化炭素の赤外線の吸収というと、 一般にもなじみのある問題は地球温暖化でしょう。 まさにここでは二酸化炭素の赤外線吸収を測っているので、 課題の 4 番では、 今回の測定結果と地球温暖化、 黒体輻射との関りを調べてみようというわけです。 こうした計算をする時、まずエネルギーの換算をしておくのが便利です。 15 °C (= 288 K) の黒体輻射の式 \eqref{eq:bbrad} は次のように書けるでしょう。

\begin{equation} \frac{I_\mrm{bd} (\tilde{\nu})}{I_0} = A \frac{\tilde{\nu}^3}{\exp (hc\tilde{\nu}/k_\mrm{B} T) - 1} = A \frac{\tilde{\nu}^3}{\exp (1.44~ \tilde{\nu}~ \mrm{cm}/288) - 1 } \label{eq:bbrad_calc} \end{equation}

このように整理しておいて（288 が 1.44 で割り切れるのもありがたい）、 \(A\) を 5 × 10^-8 cm³ ぐらいに取って計算すると、 先の呼気の赤外吸収スペクトルの図にはめ込むのにいいぐらいのサイズになるでしょう。 実際に計算してみた結果を図 6 に示します。 地球からの黒体輻射に関わって、 観測される CO₂ の赤外吸収スペクトルの中では、 低波数側の変角振動の寄与が非常に大きいことが見て取れるでしょう。

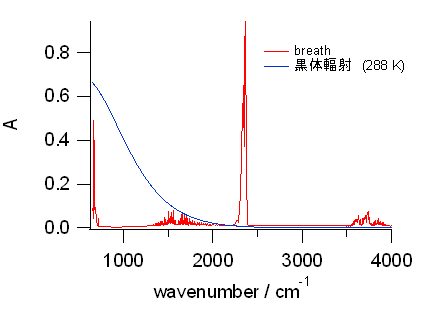
図6. 15 °C (= 288 K) の黒体輻射（青）。

このように温室効果への寄与が考えられるわけですが、 現在問題になっている温室効果の変動については、 ここでの測定結果やピーク位置の議論だけではまったく不十分です。 というのは、そもそも大気の厚みはおよそ 8 km ほどあると考えられます （大気圧が水柱にしておよそ 10 m ですから、 それに対応する 1 atm の空気の厚みは空気の密度を 1.2 mg/cm³ として（浮力補正の計算で出てきましたね） 10 m/0.0012 = 8 km）。 仮に測っている呼気中の二酸化炭素の濃度を多めに見積もって大気の 100 倍としても、 通過する距離が 10000 倍は優にありますから、 縦軸の吸光度は100 ～ 1000 倍に拡大しないといけません （ランベルト-ベールの法則）。 今回の測定で吸光度が 0.01 ぐらいの微々たる吸収でも、 大気の厚みを通せば透過率は 10 %以下、90 % 以上吸収されてしまうのです。 すでに透過率がほぼ 0 の強い吸収をさらに増しても事態に変化はありませんから、 問題はこのスペクトルではほとんど見えないような、 微妙な吸収ということになってくるのです。 また吸収量を考える上では、 吸収線の位置とともに、 その線幅も重要です。

調和振動子近似で届かない世界

「教科書的」にはこんなところまででいいのですが、 現実にはそんなに単純ではありません。 二酸化炭素の CO₂ 赤外吸収スペクトルを採録した、 NIST のデータベースから取った二酸化炭素の吸収スペクトルを図に示します。

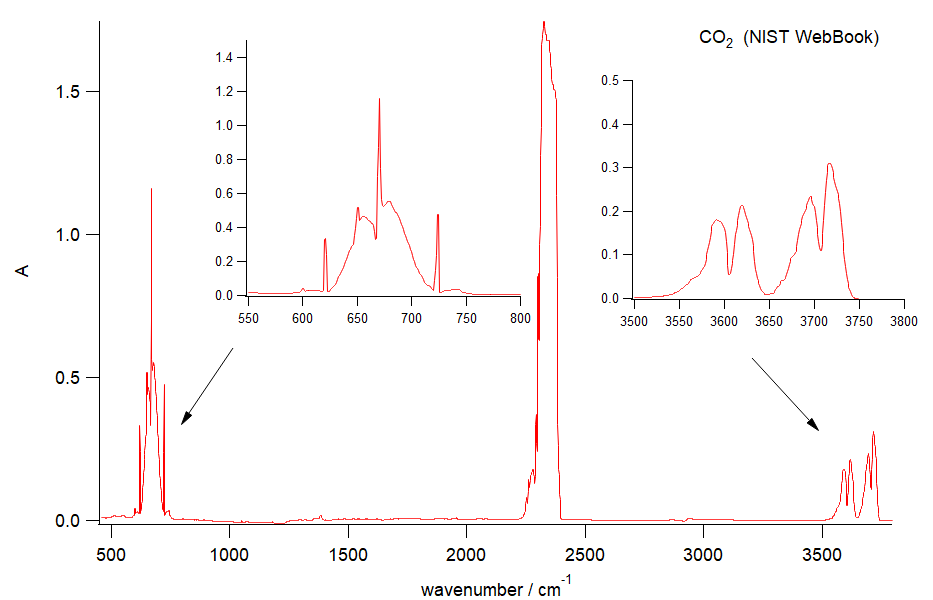
図7. NIST の WebBook の赤外スペクトルのデータから作成した、 CO₂ の赤外吸収スペクトル。 濃度が高めで、2300 cm^-1 付近の吸収は振り切れている。 Cary 630 では測れない、650 cm^-1 以下も見ると、 670 cm^-1 付近を中心にいびつな吸収があり、 3500 cm^-1 ～ 3800 cm^-1付近に２つ、 ２本に割れたピークがある。

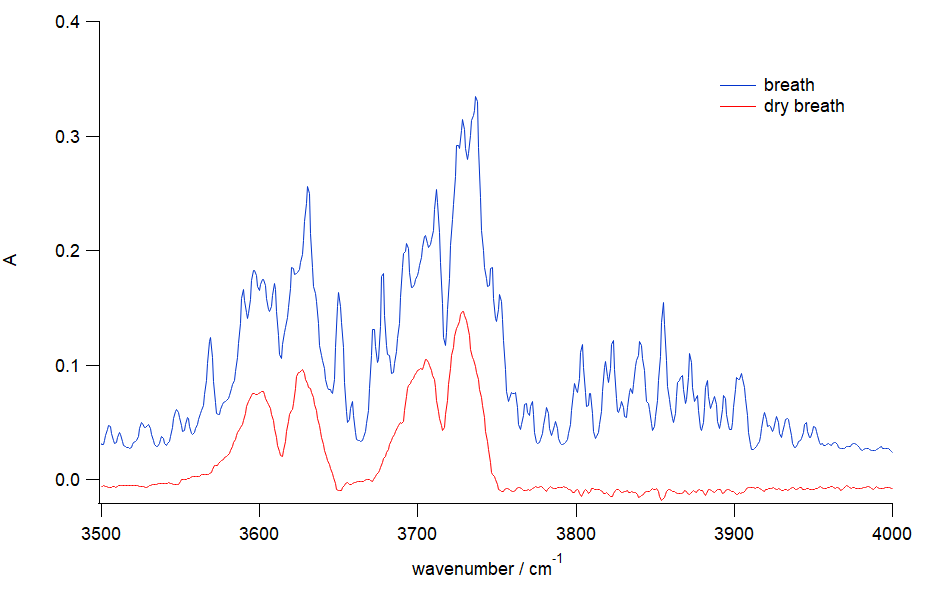
図8. 乾燥させた呼気の赤外吸収スペクトル（赤）。 乾燥させるとCO₂ による吸収がはっきり見えてくる。

実は赤外スペクトルで見られた3500 ～ 4000 cm^-1 付近の吸収には H₂O の伸縮振動（対称・逆対称）とともに、 CO₂ による吸収が共存しています。 図 8 には、ゴム管をバケツに入れた氷水に浸し、 呼気中の水分を凝縮、乾燥させて透過測定ユニットに吹き込んで得たスペクトルを示します。 得られたスペクトルには図 7 のNIST のスペクトルデータ同様、 3613 cm^-1 と 3715 cm^-1 に２つの吸収が現れています。

教科書で勉強する調和振動子モデルでは、こうした吸収は現れないはずですが、 現実の分子ではモデルにない挙動が現れてきます。 この２つの吸収にはそれ自体は表に出ていない CO₂ の対称伸縮振動も関与していて、 逆対称伸縮振動と対称伸縮振動あるいは変角振動の結合音であると帰属されています。 また地球温暖化に関わって重要なのですが、 960 cm^-1 付近、1060 cm^-1 付近にも、 同様の結合音による極めて弱い吸収が存在します。

また厄介なのは地球温暖化とも関わって重要な、 670 cm^-1 付近のいびつな吸収です。 中心のピークの周りに２本鋭いピークが見えています。 ここには CO₂ の対称伸縮振動の波数 1340 cm^-1 が変角振動の波数 666 cm^-1 のほぼ２倍になっているという事情が関わっています （いわゆるフェルミ Fermi 共鳴。 先の結合音でも、 基準振動の値の単純な足し算引き算では、 実測と合いません）。 こうした挙動は草創期の分子分光学で盛んに検討されたようです。

勉強家の皆さんの中には、参考書によって CO₂ の基準振動の値として、 ここのテキストといささか異なる値が記載されていることに悩む人がいるかもしれません。 そこにはすっきり割り切れない、 こうした事情が隠されていたりします。

いろいろな気体の赤外スペクトル

興味があれば、いろいろな気体のスペクトルを測ってみてください。 これまでに取られたスペクトルを紹介しておきましょう。

メタン・ブタン

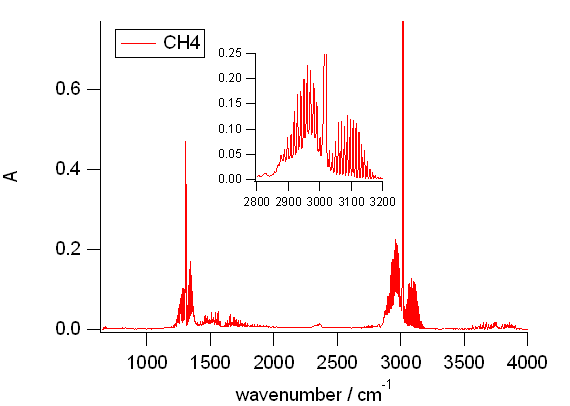
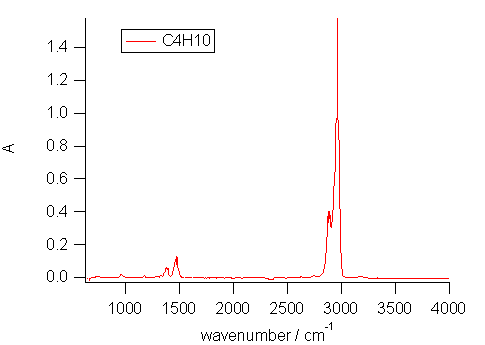
メタンとブタンのスペクトルを図 9 に示します。

実験室の都市ガスはメタンが主成分（90 %ぐらい）の天然ガス（13A型）なので、 都市ガスをポリ袋に集めて、 Cary 630 の透過型測定ユニットに流し込めば、 それでメタンの吸収が測れます （エタンなどもあるはずですが、ちょっとこのスペクトルから検出するのは難しい。 漏れ検知のために入っている付臭剤（ジメチルスルフィドなど）も同様に無理みたいです）。

ブタンは、気体の粘度の実験で使ったカセットコンロ用のボンベが残っていたので、 同様にガスを流し込んで測ってみました （ガスライターでも大丈夫）。 カセットボンベのブタンには、 蒸気圧を高めるために各社、ボンベの耐圧性も勘案しながらイソブタン（2-メチルプロパン）を配合しています （特に登山用など寒冷地仕様では比率が高く、プロパンを配合したものもある）。 今回使用したガスでは n-ブタンの比率がかなり高いようですが、 NIST のスペクトルデータを参考に調べてみると、 1480 cm^-1、1180 cm^-1 などにイソブタン（2-メチルプロパン）によるとみられる吸収がはっきり認められます。

メタンのスペクトルをもう少し見ておくと、 メタンの回転線は櫛状の構造が見え、 Q 枝に相当する鋭いピークが 1306 cm^-1 と 3018 cm^-1 に見えます。 ともに P 枝と R 枝をともなっていますが、 1300 cm^-1 付近の吸収では、先に CO₂ について見たように P 枝の方が R 枝より吸収が弱いのに、 3000 cm^-1 付近では、 逆に R 枝の方が P 枝より弱く出ているように見えます。 そこで 3000 cm^-1 付近を拡大してみると、 P 枝側に何か幅の広い吸収が重なっているように見えてきます。 といった具合に、 このあたり、分光学オタクにはたまらないところのようです。 やはりぼくには無理・・・

図9a. 都市ガス。 水上置換して採集したので水が少し出ている。	図9b. ブタン。 カセットコンロ用のボンベを使用。

エーテル

図10. 試薬瓶のキャップにエーテルを入れ、 透過測定ユニットの中に置いて、エーテル蒸気のスペクトルを測る。

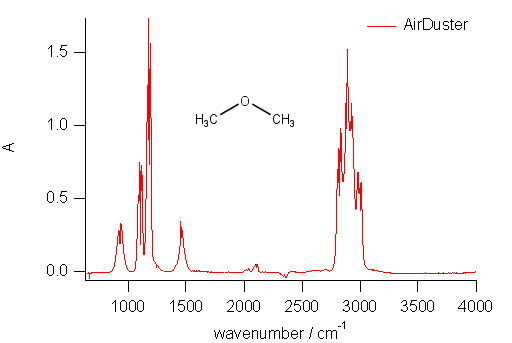
最近スプレー缶に充填するガスとして、 ジメチルエーテル（DME と略称されます。(CH₃)₂O。沸点 -24 °C）を使っているものが増えてきました （ここ10年ばかり、燃料としても注目され JIS 規格もあります： JIS K2180 燃料用ジメチルエーテル（ＤＭＥ））。 ここではエアダスターとして使用しているものを、 そのまま使って測ってみました。 市販品のエアダスターの中には燃えにくくするために二酸化炭素を配合したものもあるらしいですが、 これはほとんど純粋なジメチルエーテルのようです。

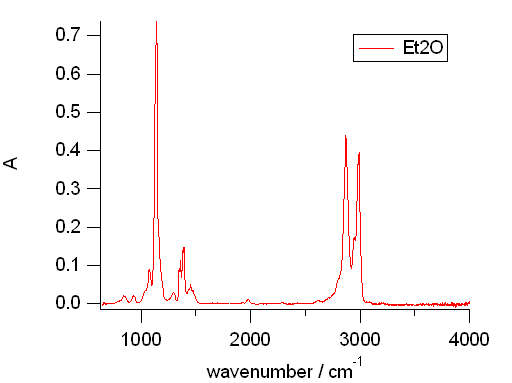
同じエーテルつながりでジエチルエーテルも、 実験室の古い在庫にあったので測ってみました。 測るのは簡単。 図 10 のように、キャップにジエチルエーテルを入れて透過測定ユニットに入れるだけです。

ちょっと見、構造の簡単なジメチルエーテルの方がにぎやかなスペクトルです。 吸収のピークが、 それぞれ回転線の影響で P Q R の３本に分裂しているように見え、 何かを物語ってくれているように見えます。 この一方、慣性モーメントの大きいジエチルエーテルの方は、 ちょっと落ち着いているようです。 こういうのもオタク心をくすぐるんでしょうね。 たぶん・・・

図11a. ジメチルエーテル。 エアダスターを使用（成分表示にはDME のみ）。	図11b. ジエチルエーテル。 小さいキャップにを入れたエーテルを測定ユニットに置いて測定。

いろいろ

有機化学の実験でも出てきた溶媒の赤外吸収スペクトルも、 エーテル同様にして測ってみました。

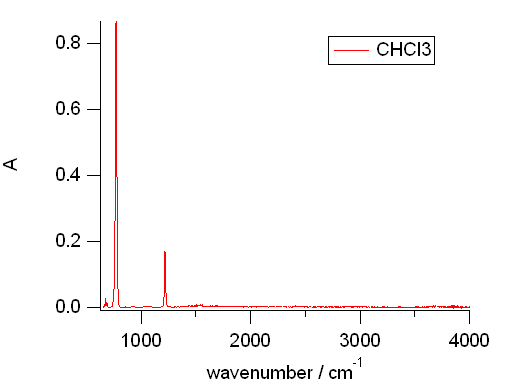
クロロホルムには目だった吸収は 773 cm^-1 と 1220 cm^-1 の２本ぐらい。 他に674 cm^-1 に小さいピークが見られます （CO₂ の変角振動のピークは 669 cm^-1）。 C-H の伸縮振動に相当する 3000 cm^-1 付近の吸収はちょっと見えません。

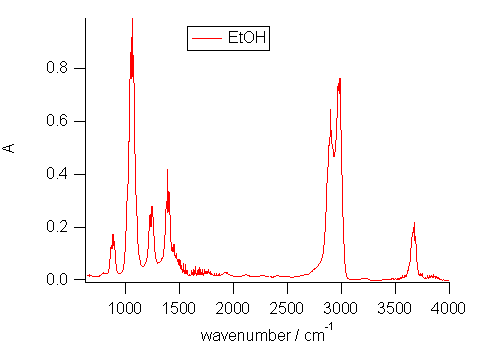
エタノールの方のスペクトルはもっと賑やかです。 有機化学で出会ったスペクトルを覚えている人は、 O-H 伸縮の吸収が 3670 cm^-1 付近に、 C-H 伸縮よりつつましやかに出ていることに驚くかもしれません。 ここら辺の話は、 後のメタノールの吸収スペクトルで取り上げることになります。

図12a. クロロホルム。	図12b. エタノール。

呼気の赤外吸収スペクトルのはなし

これまでは「教科書」で教えないことは、 見せない、見ないことにして赤外吸収の課題は実施されてきたように思います。 それは「講義」ではいいかもしれないが、 「実験」では好ましくないことでしょう。 そこでスペクトルを測って、見えること、 見えてしまうことと向き合う姿勢は持っていたいと、 こうした構成にしてみました。

何でもないことのようですが、 分光嫌いで通してきたぼくにとっては、 結構これは大変なことでした。 二酸化炭素の振動スペクトルに、 フェルミ共鳴の影響でラマンのピークが２本出るとかいう話題は、 分光嫌いの理由でありこそすれ、 およそ理解しようという対象でなかったのですが、 学生諸君相手にそうとばかり言ってはおられません。 また得られた赤外スペクトルと正面から向き合うことがなければ、 炭素の同位体に基づく吸収の存在を認識することすらなかったでしょう。 今もぼくは分光学は嫌いですが、 それでも以前よりは少し、 それに夢中になれるココロが理解できるようになったように感じています。

ともあれこの課題の中で、 学生諸君には、 赤外スペクトルの窓から見える世界を精一杯覗いてみて欲しいと思っています。 また容易にそうした世界を開いて見せてくれる、 われわれの学生時代には想像もできなかった、 この Cary 630 という装置に感謝しています。