last revised 2024.9 / 2020.10
吉村洋介
光吸収・発光と光化学反応
1.蛍光スペクトル
1.1 エネルギーの単位
分子のエネルギーは、一般に光を用いて測定されていることから、
光の真空中での波数(\(\tilde{\nu}\) )を単位として用いることも多い
(エネルギーの単位として用いられる場合、波数は媒質によらない扱いを受けることに注意)。
波数と波長 \(\lambda\) は逆数関係にあり(\(\tilde{\nu} = 1/\lambda\) )、
振動数 \(\nu\) との間には比例関係\(\nu = c\tilde{\nu}\) )(\(c\)は真空中の光速度)が成り立つ。
したがって、光量子のエネルギー\(E\)と波数 \(\tilde{\nu}\)の関係は、
\begin{equation}
E = h \nu = \hbar \omega = hc \tilde{\nu} = \frac{hc}{\lambda}
\label{eq:energy_rel}
\end{equation}
となる。ここで\(h\)はプランク定数(6.62607015 × 10-34 J s)であり、
\(\omega\) は角振動数(角速度の大きさ)で \(\hbar\) は\(h/2\pi\)(これをプランク定数とする流儀もある)。
波数は一定長さに含まれる光の波の数に対応し、単位としては通常 cm-1 が用いられる。
エネルギーの単位として用いる時には、\(hc ~\mrm{cm^{-1}}\)とするのが正確であるが、
単にcm-1と表記することが多い。
また電気的なエネルギーとの対応を見る場合には電子ボルトeV(1 eV = 1.602176634 × 10-19 J)
もよく用いられる(数値は新SIの定義による)。
1.2 蛍光スペクトル
ある試料が光を吸収し、電子基底状態(S0)から励起状態(S1)
へと遷移したとする(図1)。
この励起状態が失活するとき、そのエネルギーを光として放出したものが蛍光である。
試料に励起光を照射すると、蛍光は四方八方に放射され、蛍光測定では通常、
励起光と直角方向に放出される光を測定する。
試料溶液が清澄であれば励起光の散乱光は弱く、
光吸収・発光の効率の高い分子であれば蛍光による検出感度は非常に高く、
しばしば生理活性物質など微量成分の検出・分析に利用される。
この点、光吸収による測定は昼間の星を見るのにも似ていて検出感度は蛍光に及ばない。
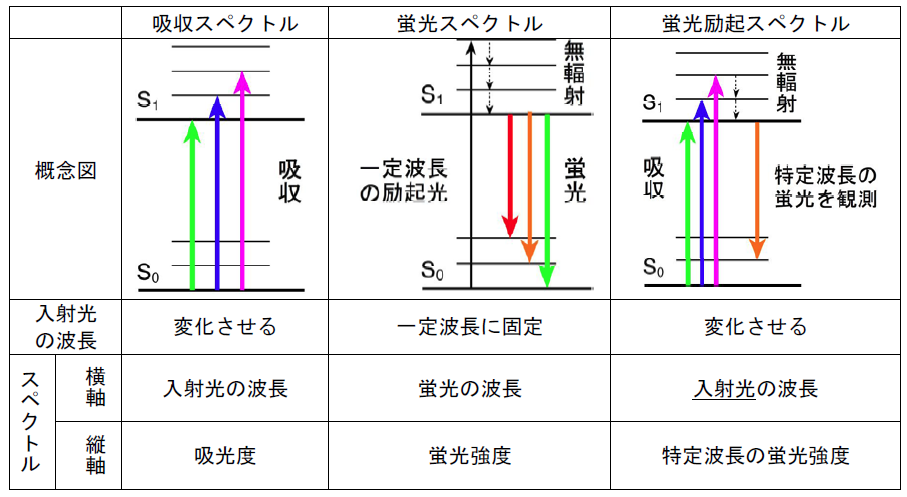
図1. 吸収スペクトル、蛍光発光スペクトル、蛍光励起スペクトルの比較
試料に光を吸収させ電子励起状態に遷移させた時、一般に分子振動等も励起されるが、
溶液などの凝縮相では周囲の分子との相互作用により、光を発せず速やかに緩和が生じる
(無輻射遷移。10-12秒程度)。
このためたいていの場合、始状態が第1励起状態(S1)の最低振動準位にほぼ限定された形で発光し(Kasha則)、
電子基底状態のいずれかの振動励起状態に達することになる。
したがって励起波長を変えても、たいていの場合、蛍光スペクトルの形状には変化が現れないし、
ある波長の蛍光強度を励起波長を変えながらモニターしたもの(蛍光励起スペクトル)は吸収スペクトルの形状と似たものとなる。
また観測される蛍光スペクトルの形状には、電子励起状態ではなく電子基底状態の振動準位がもっぱら反映される。
ある分子が発光しても、周りの分子によってその光が吸収されてしまうことがしばしば起きる。
特に励起された分子の発光が、
基底状態の同種の分子によって吸収されることによって蛍光スペクトルの形状が変化することには注意が必要である。蛍光スペクトルに対する蛍光の再吸収の影響は、
濃度を下げた測定を行うと明瞭になる。
1.3 蛍光スペクトルの表現と装置補正
蛍光スペクトルの強度\(F(\lambda)\)の表記には、いくつかの流儀がある。
特に (a) 波長\(\lambda\)を用いるか、波数 \(\tilde{\nu}\)(あるいは振動数\(\nu\))を用いるか、
(b) エネルギー強度を用いるか(以下で添え字e)、光量子数を用いるか(以下で添え字q)に注意する。
相互に次のような関係が成立する:
\begin{equation}
\lambda^3 F_\mrm{e}(\lambda) = \lambda^2 F_\mrm{q}(\lambda)
= \lambda F_\mrm{e}(\tilde{\nu}) = F_\mrm{q}(\tilde{\nu})
\label{eq:change_eq}
\end{equation}
ここで例えば\(F_\mrm{e}(\tilde{\nu})\)は波数に対するエネルギー強度分布を意味する。
吸収スペクトルについては、一般に吸光度 \(A\) あるいは透過率 \(T\) が用いられ、
たいていの場合式 \eqref{eq:change_eq} のような相互変換を要しない。
ある物質Xの吸収スペクトルと蛍光スペクトルを対比する時、
通常、吸収スペクトルについては吸光度を、蛍光スペクトルについては発光強度を取る。
これは吸光度・蛍光強度が、ともに存在するXの物質量に比例すると考えられるからである。
たとえば蛍光スペクトルの励起スペクトル(ある波長での蛍光強度を一定に保つ励起光の波長と強度の関係。
1.2参照)は、たいていの場合、吸光度のスペクトルと一致する。
一般に光の検出器の感度・回折格子の分光特性等は波長に依存する。
したがって測定結果からある程度定量的な議論をするには、
前もって標準とされる物質の蛍光スペクトルを用いて装置の較正を行う必要がある。
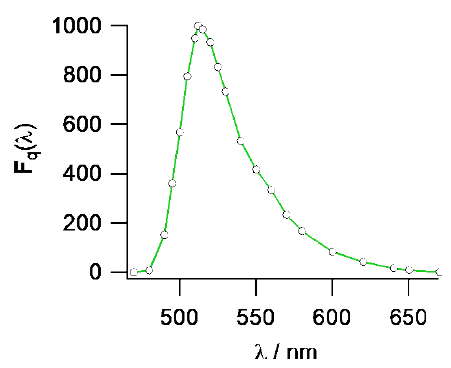
フルオレセインについては精密な測定によって、
図2のような相対蛍光スペクトル \(F_\mrm{q}(\lambda)\) を示すことが知られている。
フルオレセインの蛍光で直接較正できる範囲はおよそ500 nm~650 nmである。
蛍光スペクトルのこと
蛍光スペクトルの表示法と単位の変換公式
この課題では発光スペクトルを扱うことになります。
ここまで行ってきた光吸収による定量の課題や
赤外吸収の課題で扱ってきた吸収スペクトルと、
発光スペクトルでは大きな違いがあります。
吸収スペクトルでは、縦軸の量(吸光度あるいは透過率)は、横軸の量(波長あるいは波数)の次元が含まれませんでした。
けれども発光スペクトルで縦軸に取るのは、
単位波長(あるいは単位波数)当たりの光の強度です
(たとえば単位が W/nm になる。
さらに言えば光束か光度かといった問題もあるが以下では省略)。
また光の強度を光量子数で記述すると、
同じエネルギー量でも、波長に依存する形になります。
ですから波長を取るか波数(振動数)をとるか、
光の強度の単位をエネルギーでとるか光量子数でとるかで、
縦軸の単位、数値を変更する必要があるのです。
式 \eqref{eq:change_eq} はそうした変換をする上で、
記憶しやすい形をしています。
この変換に関わって、波長 \(\lambda\) と波数 \(\tilde{\nu}\) の変換はあまり問題ないと思いますが、
光強度の単位の変換("e" と "q")については少し暗黙の約束を考慮してもらう必要があるので、
すでに赤外分光の課題でもふれましたが、
少し(?)くどく解説しておきましょう。
確率分布関数に関わる変数変換は、次のように書くことができます
(\(X\)は\(x\)の、\(Y\)は\(y\)の確率分布関数で\(y\)は\(x\)の関数として与えられているとし、
簡単のため\(x\)と\(y\)は1対1の写像だと考える(\(y = x^2\)といったケースは考えない)):
\begin{equation}
X(x) = \left| \frac{\rmd y}{\rmd x} \right| Y(y)
\label{eq:var_chang}
\end{equation}
この関係は記号的には\(X(x) |\rmd x| = Y(y) |\rmd y|\)と書くことができ、
いわば“確率の保存”と考えればよいでしょう。
今回の波長と波数の関係式では、(暗黙のうちに)\(F(\lambda)\)は波長 \(\lambda\) の、
\(F(\tilde{\nu})\)は波数 \(\tilde{\nu}\)(\( = 1/\lambda\))のスペクトル強度を意味するとされており、
次のような関係が成り立つことになります:
\begin{equation}
F_{\mrm{e}}(\tilde{\nu}) = \left| \frac{\rmd \lambda}{\rmd \tilde{\nu}} \right| F_{\mrm{e}}(\lambda)
= \lambda^2 F_{\mrm{e}}(\lambda)
\label{eq:vl_chang}
\end{equation}
同様に\(F_{\mrm{q}}(\tilde{\nu}) = \lambda^2 F_{\mrm{q}}(\lambda)\) が成り立ちます。
さて今度は \(F_{\mrm{q}}(\lambda)\) と \(F_{\mrm{e}}(\lambda)\) の変換で、
赤外分光の課題で見たようにエネルギーを波数と同一視して取り扱うことになります。
真空中で波数 \(\tilde{\nu}\)の光の持つエネルギー\(E\)は、
光量子の数を\(Q\)とすれば次式で表わされます:
\begin{equation}
E = Qh\nu = Qhc\tilde{\nu}
\label{eq:planck}
\end{equation}
ここで \(h\) はプランク定数、\(\nu\) は振動数、\(c\) は真空中の光速です。
さて \(F_{\mrm{q}}(\lambda)\) ではエネルギー \(E\) の密度、
\(F_{\mrm{e}}(\lambda)\) では光量子数 \(Q\) の密度を扱っているので次の関係が成立します:
\begin{equation}
F_{\mrm{e}}(\lambda) = hc \tilde{\nu} F_{\mrm{q}}(\lambda)
\label{eq:eq_chang}
\end{equation}
さてここで \(hc = 1 [\mrm{E}] [\mrm{L}]\)となるような単位系を導入します。
ここで \([\mrm{E}]\) はエネルギーの単位、 \([\mrm{L}]\) は長さの単位です。
こうすることで式 \eqref{eq:eq_chang} は次のように書き換えることができます:
\begin{equation}
F_{\mrm{e}}(\lambda)/[\mrm{E}] = \tilde{\nu} F_{\mrm{q}}(\lambda) /[\mrm{L}]^{-1}
\label{eq:eq_changx}
\end{equation}
あからさまにエネルギー、長さの単位\([\mrm{E}]\) 、\([\mrm{L}]\) を書かないと約束すると次式が成立します:
\begin{equation}
F_{\mrm{e}}(\lambda) = \tilde{\nu} F_{\mrm{q}}(\lambda)
\label{eq:eq_changy}
\end{equation}
つまり \(F_{\mrm{q}}(\lambda) = \lambda F_{\mrm{e}}(\lambda)\) が成り立ち、
同様に \(F_{\mrm{q}}(\tilde{\nu}) = \lambda F_{\mrm{e}}((\tilde{\nu}))\)が成り立つこともわかります。
これらの関係をまとめたものが式 \eqref{eq:change_eq} というわけです。
式 \eqref{eq:change_eq} は \(hc = 1 [\mrm{E}] [\mrm{L}]\)となるような単位系を前提としており、
通常 \([\mrm{L}] = \mrm{cm}\) ととられるので、
波数の単位は \(\mrm{cm}^{-1}\) 、
エネルギーの単位としては\( [\mrm{E}] = hc/\mrm{cm} =~\mrm{1.986 \times 10^{-23}~ J} \)が用いられることになります
(よくある“エネルギー単位換算表”には、このあたりの事情を1 cm-1 = 1.986 × 10-23 J という風に表記してある)。
なおエネルギーを記述するのに用いられる場合、波数は媒質によらない量として扱われ、
振動数を用いて \(\nu/c\)で定義されることになります。
したがって厳密には空気中での測定で得られる波長の逆数を波数とする扱いは誤っているのですが、
空気の屈折率は1.0003でほぼ1とみなしてよいのでふつう考慮されません
(ちなみに分光器は通常、真空中の波長の値を与えるように較正される)。
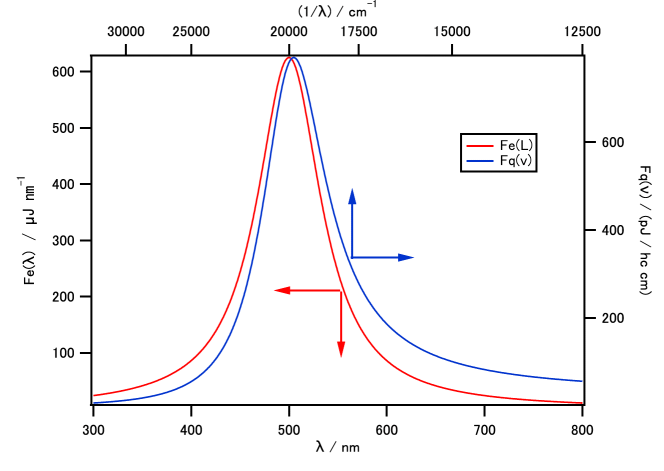
図 4. \(F_\mrm{e}(\lambda)\) を \(F_\mrm{q}(\tilde{\nu})\) に変更したことにともなう、
発光スペクトルの変化。
こうしたことを踏まえて、予習問題 1を考えると次のようになります:
\begin{equation}
F_{\mrm{q}}(\tilde{\nu})/[\mrm{L}]^{-1} = \lambda F_{\mrm{e}}((\tilde{\nu}))/[\mrm{E}]
= \lambda^3 F_{\mrm{e}}(\lambda)/[\mrm{E}]
\label{eq:pquestAx}
\end{equation}
\begin{eqnarray}
F_{\mrm{q}}(\tilde{\nu}) &=& \lambda^3 F_{\mrm{e}}(\lambda) /[\mrm{L}] [\mrm{E}] \\
&=& \frac{\lambda^3}{(\lambda - \mrm{500~ nm})^2 + \mrm{1600~ nm^2}} ~ \mrm{J~nm} / hc \nonumber \\
&=& \frac{40~ \tilde{\nu}^{-1} \mrm{cm}^{-1}}{(\tilde{\nu} - 20000 ~\mrm{cm}^{-1})^2 + 0.0064 ~\tilde{\nu}^2} ~ \mrm{J} / hc
\label{eq:pquestAy}
\end{eqnarray}
発光スペクトルをエネルギー-波長表示 \(F_\mrm{e}(\lambda)\) から、
光量子-波数表示 \(F_\mrm{q}(\tilde{\nu})\) に変換することによる発光スペクトルの変化を、
図 4 に示します。
変換にともなう発光スペクトルの極大波長(波数)の変化が分かるように、
波数表示の結果も波長軸上に合わせて表示していますが、
エネルギー-波長表示では発光極大が 500 nm (20000 cm-1)であったのが、
光量子-波数表示では 505 nm(19809 cm-1)と長波長側に移動することになります。
発光スペクトルの議論では、
極大波長(波数)を議論することが多いのですが、
詳細な議論ではこうした点も押さえておく必要があります。
表示の変換による極大波長(波数)のシフトは、
黒体輻射のようにスペクトルのピークがなだらかな場合には大きくなり、
ウィーン Wien の変位則で通常用いられるのはエネルギー-波長表示 \(F_\mrm{e}(\lambda)\) にもとづくもので
\(\lambda_\mrm{max} T = 2.90 ~\mrm{mm~ K}\)ですが、
エネルギー-波数表示 \(F_\mrm{e}(\tilde{\nu})\) であれば
\(T/\tilde{\nu}_\mrm{max} = 0.510 ~\mrm{cm~ K}\)になって
(赤外分光の課題ではこの形でした)、
\(\lambda_\mrm{max} \tilde{\nu}_\mrm{max} \ne 1\) です。
ただしアントラセンの蛍光スペクトルでも調べてもらいますが、
われわれが通常「ピーク」と呼ぶようなものについては、
たいていの場合、極大波長は極大波数の逆数と見なして問題はありません。
蛍光スペクトルの較正
取りあえず、分光光度計というのはある波長 \(\lambda\) の光を受け取った時、
受け取った光のエネルギー \(E(\lambda)\) に比例した電流 \(i(\lambda) = k(\lambda) E(\lambda)\) を出す装置だと思っていいでしょう
(光の強度が強くなりすぎると比例しなくなりますが・・・)。
吸光度の測定であれば、
入射光と透過光の強度比を取るので、
比例関係が満たされておればそれでよいのですが、
蛍光の場合、この光の強度自体を問題にするので、
この比例定数 \(k(\lambda) \) の波長依存性が問題になります。
そこで少し精密なスペクトルの検討、
あるいは異なる機種で得られた蛍光スペクトルとの比較をしたりする分には、
標準物質の蛍光スペクトルを測ることで装置の特性を調べ、
較正を行う必要があるのです。
ここではフルオレセインの蛍光を用いた、
較正操作の一端に触れてもらいます。
テキストに紹介している標準スペクトルのデータは CSV ファイルの形で提供します。
ここに与えられている標準スペクトルは0.1 mol/L水酸化ナトリウム溶液中で、
波長・光量子数表示 \(F_\mrm{q}(\lambda)\) を用いた相対強度になっています。
今回の実験はpH 10の炭酸塩緩衝液中で行いますが、スペクトルの形状に変化がないものとして取り扱うことにします。
今回の場合、較正曲線 \(C(\lambda)\) はこの標準スペクトル \(F^{*}_\mrm{q}(\lambda)\) が、
CHEMUSB4で観測されるフルオレセインの蛍光強度\(S^{*}(\lambda)\) と550 nmで一致するものとして描いてもらえばよいでしょう。
つまり
\begin{equation}
C(\lambda) = \frac{F^{*}_\mrm{q}(\lambda)}{S^{*}(\lambda)} \frac{S^{*}(550~\mrm{nm})}{F^{*}_\mrm{q}(550~\mrm{nm})}
\label{eq:FL_corr}
\end{equation}
を作っておけば、他の試料について観測される蛍光強度\(S(\lambda)\) について、
\(C(\lambda) S(\lambda)\)は波長・光量子数表示 \(F_\mrm{q}(\lambda)\) で表示した、
相対的な蛍光スペクトルを与えることになるわけです。
テキストにあるように、励起された分子の発光が、基底状態の分子によって吸収されることによって蛍光スペクトルの形状は変化します。
今回の装置較正に当たっては、510 nm以下の領域についてはこの点に留意する必要があります。
なお以降の実験でCHEMUSB4で得られる蛍光強度スペクトルには、
ここで得た \(C(\lambda) \) を用いて較正を行っておくのが望ましいのですが、
定性的なレベルの実験であり、
また較正できる波長範囲が限られているので較正しないでよいことにしています。
スプライン補間:データの内挿
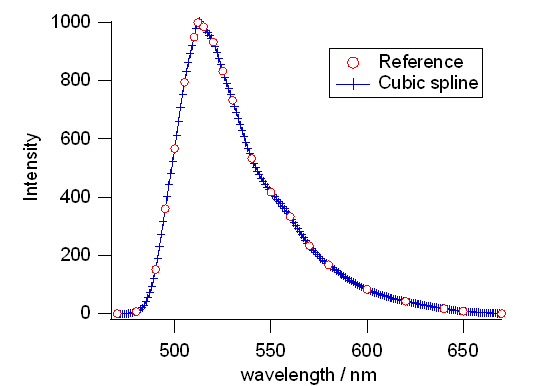
図 5. フルオレセインの標準蛍光スペクトルデータを、
スプライン補間して 1 nm 間隔のデータにした結果。
今回扱うフルオレセインの標準蛍光スペクトルのようにデータが飛び飛びの点で与えられ、
その中間地点のデータを推定する必要に迫られることがあります
(以下では等間隔ではない{(x[i], y[i])} (i = 1, 2, …, N)というデータを考えます)。
このようなデータの補間(内挿。interpolation)法として、今日一般に用いられるのはスプラインspline関数を用いる手法です。
よく用いられる単純なスプライン関数は、各データ区間[(x[i], y[i]), (x[i+1], y[i+1])]を3次関数で補間し、
各データ区間の間で1次と2次の微係数が一致するように定め、
両端点(i = 1, N)で2次の微係数が0となるようにします
(「3次の自然スプラインnatural cubic spline」と呼びます。
全部で4×(N - 1)の3次方程式の係数を決める必要があり、各区間2個のデータ点を通ることから2×(N - 1)、
区間の間で微係数が一致することから2×(N - 2)の条件式、
それに両端での条件2つを付加すれば、係数はすべて決まる)。
通常の科学技術用のソフトにはこうした補間手続きが組み込まれており、
IgorではメニューからAnalysis → Interpolate... を開き、Interpolation TypeでCubic Splineを選べばよいわけです。
なお実際に得られたフルオレセインのスペクトルと補間して得た標準スペクトルを比較する際には、
まず両者を1 nm間隔のデータにしておくのがよいでしょう
(標準スペクトルは470 nmから670 nmの範囲について与えられているので、補間する時にDestination Pointsを201にする)。
またフルオレセインの蛍光スペクトルデータは、用意されているマクロで正規化すると250 nmから800 nmまで1 nm間隔のデータ(ahとします)になっているはずです。
ここから470 nmから670 nmの範囲のデータを切り出すには、新しいwave(bkとします)を用意し、
Command Windowでbk = ah[220+p]としてやればよいのです
(p は bk の対応する行数を表す)。
実際の較正曲線
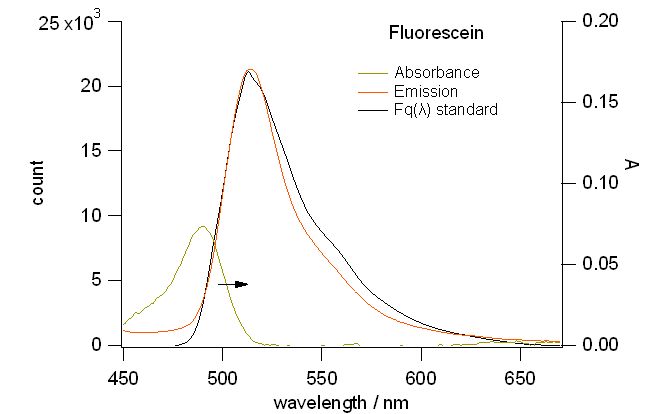
図6. CHEMUSB4 で得たフルオレセインの蛍光スペクトル(橙色)と、
文献に与えられた標準スペクトル \(F_\mrm{q}(\lambda)\) (黒線)。
440 nm 励起。光源が強かっため、迷光の影響が現れている。
この課題ではフルオレセインを用いて装置較正を行ってもらうわけですが、
ちょっと先回りして、えられたフルオレセインの蛍光スペクトルを、
図 6 に紹介しておきます。
CHEMUSB 4 で得られるフルオレセインの蛍光は、
標準スペクトル \(F_\mrm{q}(\lambda)\) とまずまず合致していますが、
長波長側で少し発光強度が弱めに出ているようです。
では他の波長領域ではどうか?
もう少し短波長側 400 ~ 500 nm について、
硫酸キニーネを用いて行った結果を図 7 に紹介しておきます。
硫酸キニーネは蛍光物質として古くから知られ
(有名な1852年のストークスの蛍光の研究は、
キニーネの蛍光に触発されたようです)、
フルオレセインなどとともに蛍光スペクトルの較正によく用いられます。
キニーネについて CHEMUSB 4 で得られる蛍光スペクトルは、
標準スペクトルからかなり外れていて、
蛍光の極大波長などもかなりずれた値となっています。
400 ~ 600 nm に蛍光が現れること自体はよいのですが、
鏡像関係やストークスシフトなど、少し踏み込んだ議論になると問題がでてきます。
ちなみにStokes の論文のタイトルは
「光の屈折率の変動について On the Change of Refrangibility of Light」。
当時はまだ光の波動説と粒子説がせっていたらしく、
蛍光現象を複屈折などの現象と関連付けて理解しようと試みてもいたようです。
さまざまな物質についての蛍光の検討や
(中にはクロロフィルの蛍光もある "solution of leaf-green in alcohol")、
蛍光では偏光が解消されるといった実験もすでに行われており、
興味深い内容なのですが、"internal dispersion" など、
ぼくにはそのあたりの論の進め方は読み込めませんでした。
専門の方のご教示を仰ぎたいところです。

|
|
|
図7a. 硫酸キニーネの蛍光。
Stokes の論文に "beautiful celestial blue colour"
とあるように、
400 nm ぐらいの波長のブラックライトの照射で、
「天空の青」と称したい美しい蛍光が現れる。
|
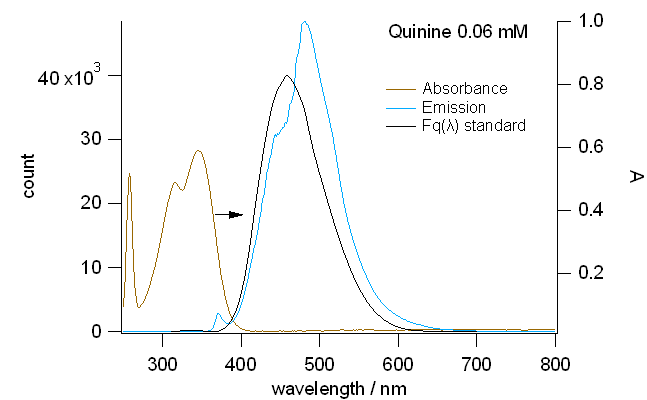
図7b. 硫酸キニーネの溶液の吸収スペクトル(ウグイス色)と CHEMUSB4 で得た蛍光スペクトル(水色。370 nm 励起)。
図中の黒線は文献に与えられた標準スペクトル \(F_\mrm{q}(\lambda)\) 。
CHEMUSB4 で得た蛍光スペクトルは、標準スペクトルより長波長側にピークがあり、
450 nm 付近に肩があるようには見えるけれども、
これでは吸収と発光の極大波長の差(ストークスシフト)が正しく出てこない。
|
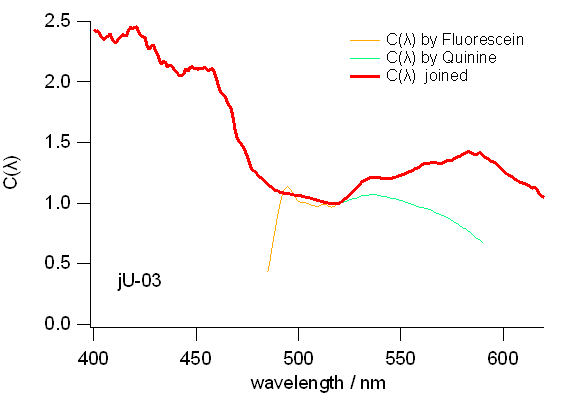
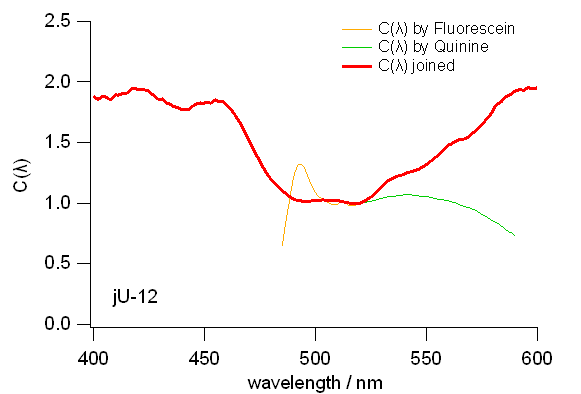
キニーネを用いて作成した較正曲線と、フルオレセインを用いて作成した較正曲線とを、
520 nm でつないで作成した較正曲線を、
jÜ-03 号機と jÜ-12 号機について図 8 に示します。
較正曲線の大まかなプロフィールは似通っていますが、
同じCHEMUSB 4 でも異なる機体では、較正曲線は若干違います。
また励起光の照射強度、照射方向によって迷光の強度が異なり、
標準物質の蛍光の極大から離れるにしたがって、
較正曲線は大きな影響を受けるようになります
(キニーネとフルオレセインで、それぞれの蛍光強度の弱いところで、
較正曲線の値が一致しないのはそのため)。
今回の蛍光の定性的な実験ではあまり本質的ではありませんが、
蛍光測定専門の装置では、
検出器の感度の高いことは無論、
こうした問題にも十分な配慮をしてあるわけです。
|
|
|
図8. キニーネを用いて作成した較正曲線と、フルオレセインを用いて作成した較正曲線とを、
520 nm でつないで作成した較正曲線。
左は jÜ-03 号機、右は jÜ-12 号機についてのもの。
同じ CHEMUSB 4 でも機体が異なると、
較正曲線は若干異なる。
また標準物質の蛍光の極大から離れるにしたがって、
迷光の影響で較正曲線の値は小さめになっていく。
|
光化学のページへ