| 図 1. 時計反応の様子。 8 mmol/L の亜硫酸水素ナトリウム溶液に、 4 mmol/L になるようにヨウ素酸カリウム溶液を加える。 ここでは 1 分弱で発色している。 |
時計反応 clock reaction というのは、いわば「時限爆弾」のような反応で、 一見変化の見られない静止期(誘導時間)を経た後、 突如、急激な変化を示す反応です。 さまざまな種類の時計反応が知られていますが、 反応の容易さ(普通の化学実験室なら備えている試薬を2種類混ぜるだけ)、 変化の明瞭さを考えると、 元祖ランドルト Landolt の研究したヨウ素酸-亜硫酸系にまず指を屈するところで (ランドルト反応とも呼ばれます)、 単に時計反応と呼べば、(ぼくの世代ぐらいは)たいていこのヨウ素酸-亜硫酸の反応を指します。
ぼくが実験課題について説明する時に使っていた時計反応(ランドルト反応)の動画を、図 1 に示しましょう。 1 分弱、反応の背景を簡単に述べ終わったころ発色するのですが、 時計反応を初めて見るという学生も多く、結構受けが良いです。 時計反応は手軽にできて廃液処理もかんたん。 高校の授業でやるとすれば 30 分もあれば収まり、 高校レベルの化学反応速度の実験の定番で、 みんなおなじみかと思っていたら意外に知られていないようです。 時計反応は一見、無から有を生じるもののようにも見えます。 けれどもその背後では、種々の反応が起きています。 この実験課題では、何も起きていないように見える最初の静止期にも、 また発色した後も、 着々と反応が進行していることを、電気伝導度を測ることで調べてもらうことになります。
テキストの解説にもありますが、 時計反応(ランドルト反応)の構成要素として、次の3つの反応式を挙げることができます ((3) の反応の量論係数は、取り扱いが簡単になるように通常の表記より 3 倍してあります)。
| IO3- + 3 HSO3- → I- + 3 HSO4- | (1) |
| IO3- + 6 H+ + 5 I- → 3I2 + 3 H2O | (2) |
| 3I2 + 3 HSO3- + 3 H2O → 6I- + 6 H+ + 3 HSO4- | (3) |
このように3つの反応を挙げているわけですが、 最初にヨウ化物イオン I- を加えていないので、 (2) の反応、そして (3) の反応は起きようがありません。 でも一旦 (2) の反応が進みだすと、(3) の反応でヨウ化物イオン I- と硫酸水素イオン HSO4- が生み出されます。 (3) の反応は速やかに進行し、 (2) の反応の反応物であるヨウ化物イオン I- と水素イオン H+(硫酸水素イオン HSO4-)が拡大再生産されていき、 (2) → (3) → (2) …… というプロセスが進行します。 こうした反応を自己触媒反応と呼びます。 (1) の反応は、この自己触媒反応の初動となる反応(開始反応と呼ぶことにします)になっていて、 ヨウ素酸の還元反応はもっぱら、(2)+(3) の自己触媒反応で進行します。 そして亜硫酸水素イオン HSO3- が反応し尽くすと (3) の反応は停止、 時計反応の誘導期が終わり、ヨウ素 I2 が生成して発色が起きます。 この (2)+(3) の自己触媒反応で進行することが、急激な発色という時計反応としての性格を与え、 また反応物(亜硫酸水素イオン HSO3- )を多く投入するほど、 反応物が急速に消失する(誘導時間が短くなる)という一見不思議な現象をもたらします。 なお硫酸水素イオン HSO4- は解離して、水素イオンH+ と硫酸イオン SO42- になります(硫酸水素イオンの pKa は 2.0 )。 また亜硫酸水素イオン HSO3- は中和されて亜硫酸 H2SO3(H2O + SO2)になります (亜硫酸の pKa は 1.9)。 こうした酸解離反応も時計反応の重要な要素ですが、 まずは置いておきます。
時計反応でヨウ素による発色が現れるまでの誘導時間について、ちょっと詳細に(くどく)ぼくなりの説明をしておきましょう。 まず (1) の反応式の持つ意味合いに注意してください。 ここでは (1) の反応は、(2) + (3) の自己触媒反応を起動する開始反応を意味していますが、 見た目に変化のない静止期(誘導期)の反応を総体的に捉えたもの((2) + (3) が (1) になる)とみることもできます。 このことがしばしば混乱のもとになります。 事態をはっきりさせるには、各反応それぞれの反応進行度を考えるのがよいでしょう。 体積一定とみなしてよいので、 (1)、(2)、(3) の各反応の反応進行度を体積で割ったものを、それぞれ z1、z2、z3 とすると、 ヨウ素酸イオン、硫酸水素イオン、ヨウ化物イオン、ヨウ素の濃度について、次のような関係が成り立ちます (ヨウ化物イオン、ヨウ素の初濃度を 0 にとっています [I-]0 = [I2]0 = 0):
| [IO3-] = [IO3-]0 - z1 - z2 | (4) |
| [HSO3-] = [HSO3-]0 - 3z1 - 3z3 | (5) |
| [I-] = z1 - 5z2 + 6z3 | (6) |
| [I2] = 3z2 - 3z3 | (7) |
こうすると時計反応で発色するまでの段階、 誘導期における反応進行度の関係を次のように整理できます。 まず発色しておらずヨウ素がないわけですから([I2] = 0)
| z2 = z3 | (8) |
亜硫酸水素イオン HSO3- が存在する限り、誘導期は続きます。 ですから誘導時間 tC は、次の関係が満たされるまでの時間ということになります( 実験で初濃度は [IO3-]0 > 3[HSO3-]0 となるように設定します)。
| [HSO3-]0 = 3z1 + 3z2 ≈ 3z2 | (9) |
ここで 発色の時点(誘導時間)で (1) の開始反応の反応進行度は (2) より十分小さい z1 ≪ z2 としています。
量論について整理したので、 反応速度のプロフィルを少し具体的に見ておきましょう。 誘導期においては、(1) の誘導反応について次のような速度則が
\begin{equation} \frac{\rmd z_1}{\rmd t} = k_1 \mrm{[H^{+}]}~\mrm{[IO_3^{-}]}~\mrm{[HSO_3^{-}]} \tag{10} \label{eq:rate_ini} \end{equation}
また (2) の反応については、次のような速度則が成り立つことが知られています。
\begin{equation} \frac{\rmd z_2}{\rmd t} = k_2 \mrm{[H^{+}]^2}~\mrm{[IO_3^{-}]}~\mrm{[I^{-}]^2} \tag{11} \label{eq:rate_dush} \end{equation}
ここで k1、 k2 はそれぞれの反応の速度定数です。 ここで注意しておくべきは、(2)+(3) の自己触媒反応について、 反応速度が、生成物である水素イオン H+(硫酸水素イオン HSO4-)、 ヨウ化物イオン I- の濃度に依存することになることです。 原因(反応)が結果(生成物)に依存するというのはいささか奇妙ですが、 こうしたところが「化学反応論 chemical kinetics」の面白いところです。 また亜硫酸水素イオンの減少速度が、 亜硫酸水素イオンの濃度に依存しないこと(0 次反応)も注意しておいてよいでしょう (z3 = z2 なので 3 dz3/dt = 3 dz2/d t )。
ヨウ素の発色が起きるまでの誘導期は、 最初 (1) の開始反応がもっぱら起きている期間と (2)+(3) の自己触媒反応がもっぱら起きている期間に分けて考えることができます。 この切り替えが起きる時間を tX、またその時の (2) 反応の反応進行度を zX とします。 (2)+(3) の自己触媒反応は反応生成物が反応を促進するので、爆発的に反応が進行することになりますが、 その様子を見てみましょう。
|
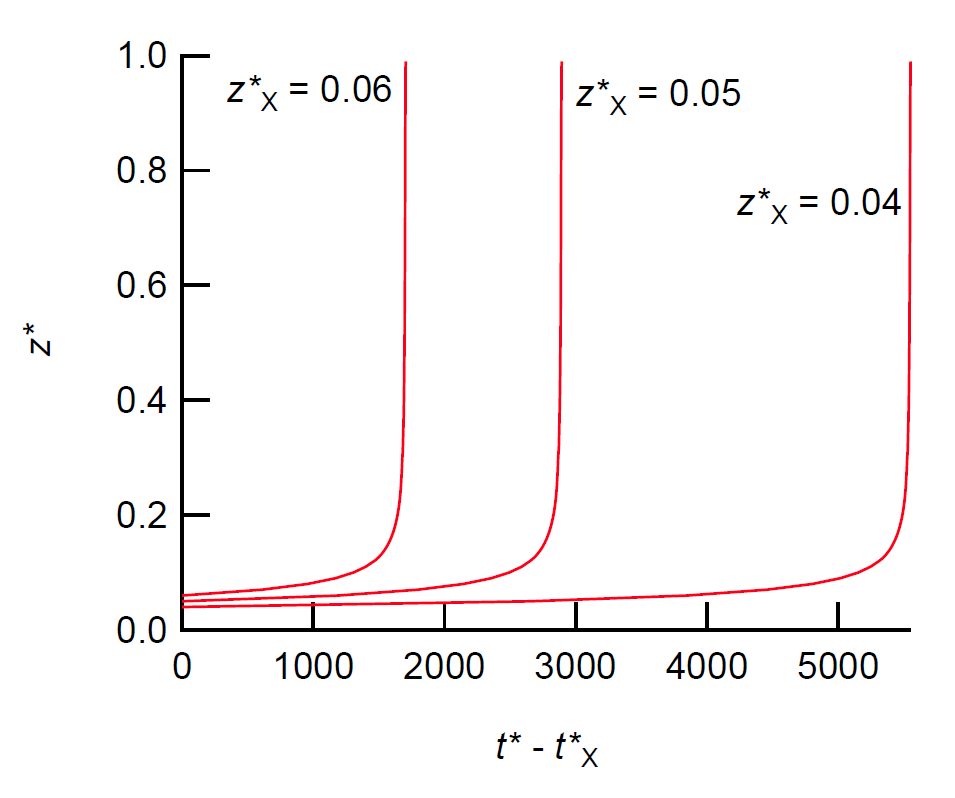
| 図 2. 自己触媒反応による反応進行度 \(z^* = z_2/a\) の時間変化。 \(t^{*} = 9k_2 a^4 t\) で \(a = \mrm{[IO_3^{-}]}_0\) としています。 時間経過とともに反応速度が急増し、 誘導反応から自己触媒反応への乗り換えが起きる時点での反応進行度 z*X によって、反応進行度が急増する時間は大きく変化します。 |
自己触媒反応が支配的な期間では、z1 ≪ z2 であり、 水素イオン濃度が生成する硫酸水素イオン濃度とほぼ等しいとすると(\(\mrm{[H^{+}]} \approx 3z_2\))、 先の式 \eqref{eq:rate_dush} の速度則 は次のように書けます:
\begin{equation} \frac{\rmd z_2}{\rmd t} \approx 9k_2 ~(a - z_2)~z_2^4 \tag{12} \label{eq:rate_autox} \end{equation}
ここで簡単のため \(a = \mrm{[IO_3^{-}]}_0\) としました。 \(z^{*} = z_2/a\)、 \(t^{*} = 9k_2 a^4 t\) として、 この微分方程式を解くと、次のような自己触媒反応による反応進行度の時間変化の表現が得られます。
\begin{equation} t^* - t^*_{\mrm{X}}= \left[ \ln \frac{z^*}{1-z^*} - \frac{1}{z^*} - \frac{1}{2{z^*}^2} - \frac{1}{3{z^*}^3} \right]^{z^*}_{z^*_{\mrm{X}}} \tag{13} \label{eq:rate_autoy} \end{equation}
式 \eqref{eq:rate_autoy} に従って、反応進行度 \(z^{*} = z_2/a\) の時間依存性を図示すると、 図 2 のようになります。 自己触媒反応への乗り換えが起きた後、 しばらく時間が経過すると、急激な反応の進行が起きます。 時計反応で硫酸水素ナトリウムの初濃度([HSO3-]0)は、 ヨウ素酸カリウム(a = [HIO3-]0)の半分から2倍くらいなものですから、 (9) 式より誘導時間までの反応進行度 z* は 0.2 以上です。 図 2 を参照すると、この程度の反応進行度であるなら、自己触媒反応への切り替えが起きる反応進行度 \(z^*_{\mrm{X}}\) が同じなら、 誘導時間にはほとんど差がありません。 自己触媒反応への切り替えが十分小さい進行度で起きるとした時、 誘導時間 t*C は式 \eqref{eq:rate_autoz} のように表すことができます。
\begin{equation} t^*_{\mrm{C}} \approx \frac{1}{3{z^*_{\mrm{X}}}^3} \tag{14} \label{eq:rate_autoz} \end{equation}
ここで切り替え時間 t*X は誘導時間 t*C に比べて無視でき、 z*X = zX/a は 1 より十分小さいとしました。 式 \eqref{eq:rate_autoz} は、元の表式に直すと次のようになります:
\begin{equation} 9k_2 a t_{\mrm{C}} \approx \frac{1}{3{z_{\mrm{X}}}^3} \tag{15} \label{eq:rate_autou} \end{equation}
さてここで問題なるのが (1) の開始反応から (2)+(3) の自己触媒反応に移行する時点での反応進行度 z*X ですが、 おおまかに (1) の反応速度と (2)+(3) の反応速度が等しくなるところだと考えてよいでしょう。 そこで大胆に次のように仮定します。
\begin{equation} k_1 z_{\mrm{X}} a \mrm{[HSO_3^{-}]_0} \approx 9 k_2 a z_{\mrm{X}}^4 \tag{16} \label{eq:rate_autov} \end{equation}
この式と先の自己触媒反応の式 \eqref{eq:rate_autou} から、 誘導時間 \(t_{\mrm{C}}\) は次式で評価できます。
\begin{equation} t_{\mrm{C}} \approx \frac{1}{3 k_1 \mrm{[IO_3^{-}]_0} ~\mrm{[HSO_3^{-}]_0}} \tag{17} \label{eq:rate_autow} \end{equation}
きわめて単純化した乱暴なお話ですが、誘導時間はヨウ素酸カリウム、 亜硫酸水素ナトリウムの初濃度にそれぞれ反比例するという結果となります (というか、そうなるように式を ”誘導” しています)。 加えた亜硫酸水素ナトリウムが多いほど、 自己触媒反応が支配的となる反応進行度 z*X が大きく、 誘導時間が短くなるのです。
log [IO3-]e + 5 log [I-]e = 6 pH - 55.73
平衡は pH に強く依存し、時計反応の条件では溶液の pH が 4.5 ぐらいなので反応が進行しますが、 pH 7 ぐらいになると、反応はほとんど進みません。
反応 (2) の反応速度については、 古くダッシュマンの研究があり、反応 (2) はダッシュマン Dushman 反応とも呼ばれます。 一方逆反応の速度が遅いため、一度ヨウ素が生成すると、塩基を加えて pH を上げても、ヨウ素は容易には消失しません。 このことを利用して、 近年、マイクロリアクターでの反応溶液の混合の効率を評価するモデル反応として注目され、 その道ではビラモー Villermaux・ダッシュマン反応と呼ばれることが多いようです。
この時計反応の実験の準備で重要なのは、 0.1 mol/L の亜硫酸水素ナトリウム NaHSO3 溶液を作り置きしないことです。 調製したての pH は、(pK1 + pK2)/2 ≈ 4.5 程度になります。 それが空気酸化を受けて pH が下がり、半年ぐらいも置いておくと、pH 2.0 ぐらいになっていることもありました。 時計反応は pH に敏感で、 pH の低下は、異様に短い誘導時間として現れます。 ですから 0.1 mol/L 亜硫酸水素ナトリウム NaHSO3 溶液は、 実験のたびに 100 mL 調製するだけに止めるようにしています。 この点、ヨウ素酸カリウム KIO3 溶液は安定で、 数年分を作り置きしておいても問題ありません。
| 図 3. 時計反応の誘導時間の測定の様子。 混合後 3 分経った当たりから発色まで。 混合後、静置するグループもあれば、 試験管を振りながら辛抱強く調べるグループもあります。 |
誘導時間の測定は例によって、思い思いの趣向で挑戦してもらっています。 図 3 に典型的な観察の様子を示します。 テキストに設定してある、それぞれ 0.02 mol/L のヨウ素酸カリ KIO3・亜硫酸水素ナトリウム NaHSO3 溶液と水の混合比 1:1:3 の場合、 典型的には誘導時間は 3 分を超え、このあたりが、 だいたい我慢の限界のようです。 誘導時間の測定は、テキストには試験管でやることになっていますが、 ポリカップでやってみるのも別に止めません。 デンプン溶液は特に入れる必要はありませんが、 濃度が低い場合、誘導時間の出現がはっきりします。 また変色後放置しておくと、色が青紫から褐色に変わるというのも、 面白いところです (ヨウ素デンプン反応は、ヨウ化物イオンがないと発色しません)。
ただし誘導時間を事細かに、0.1 s まで測ろうというのは、 あまり意味がありません (ストップウォッチまで用意して ”煽って” いますが・・・)。 そもそも混合の際に、瞬時に均一にすることはできません。 たとえばヨウ素酸カリ KIO3 溶液・亜硫酸水素ナトリウム NaHSO3 溶液と水を 2 : 2 : 1 で混合する時、 最初にヨウ素酸カリ溶液と亜硫酸水素ナトリウム溶液を混ぜてから水を入れるのと、 水にヨウ素酸カリ溶液と亜硫酸水素ナトリウム溶液を入れるのとでは結果が大きく違ってきます。
誘導時間の測定は目視で行ってもらいますが、 吸収スペクトルを測定することも考えられます。 図 4 には、希薄なケースについて、 吸収スペクトルの時間変化を調べた結果を示します。 誘導時間が過ぎると、目視での発色に対応して、 吸光度の急速な増加が起きていることが分かります。 また紫外部の吸収に注目すると、 吸光度の急速な増加の後、ゆるやかな減少が見られます。 これは三ヨウ化物イオン I3- の、 ヨウ素 I2 の生成にともなう増加と、 ヨウ化物イオン I- の消失にともなう減少に対応しています。

|

|
| 図 5a. 電気伝導度測定装置の作成例。 電極は電気分解の実験でも使ったステンレス線を適当に切って作りましょう。 | 図 5b. 電気伝導度の測定の様子。 これからヨウ素酸カリウム溶液を投入するところ。 いささか雑然としていますが、測れればそれが正解。 |
反応の追跡は、電気伝導度を測定することで行ってもらいます。 電気伝導度の測定は、図 5 のような簡単な装置で行います。 実験の詳細は3回生実験の物理化学・物性化学実験の準備の中で紹介していますので、 参照してください。 この実験の反応の濃度設定は、 誘導時間の実験のヨウ素酸カリウム溶液、硫酸水素ナトリウム溶液、水が 1:1:5 というのと同じですから、 試験管で行った実験と同じ誘導時間を示すと期待していると、たいてい 1 分くらいずれます。 先に触れましたが、時計反応の誘導時間は、濃度が低くなると、 再現性が乏しくなります。 特にここでの実験のように、容器が違ったり、液量が違ったりすると、 混合初期の状況が変化し、再現性がよくないようです。
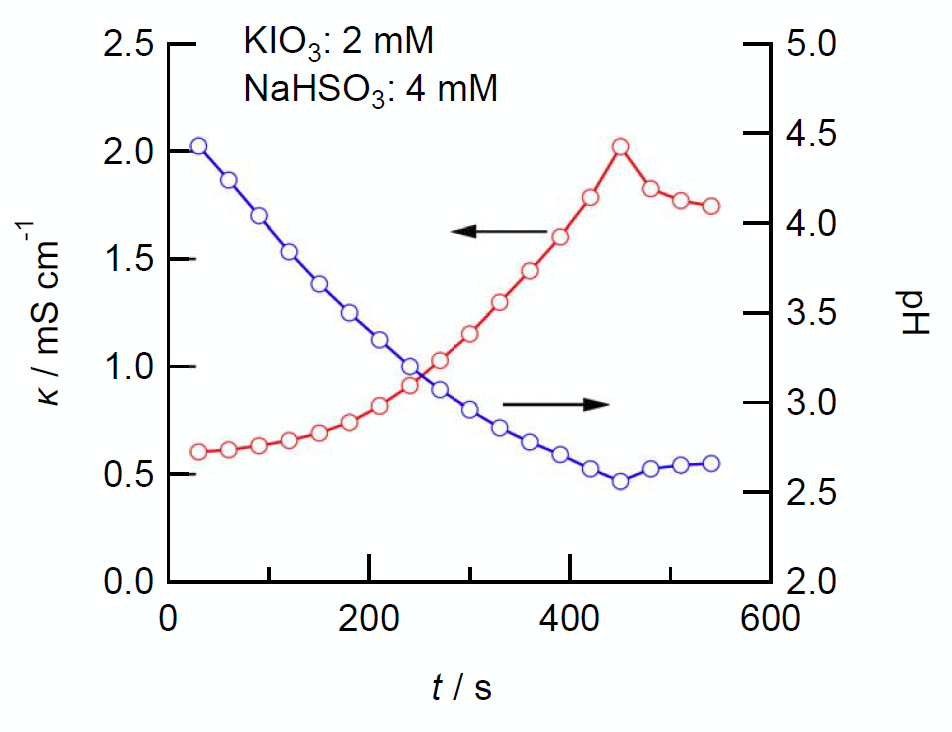
実際のセットアップでの電気伝導度の測定例はテキストに載せたので、 ここでは実験室のイオン交換水のチェックに使っている簡易な電気伝導度計を使って行った測定結果を図 6 に紹介しましょう。 図には pH の結果も載せてあります。 pH に見る水素イオン濃度の増減が、電気伝導度にそのまま反映されている様子が見て取れるでしょう。 誘導期の終了、ヨウ素の発色が起きるまで (2)+(3) (あるいは (1) )の反応による水素イオン濃度の増加が起き、 そこから (2) の反応による水素イオンの減少に転じます。 また誘導期間の終了に向けて加速度的に反応が進行するという、 先の「時計反応のしくみ 」の節でみた、 自己触媒反応の特徴が見て取れます。 ただし図 2 で見るような、 極端な反応の加速は起きていません。 これは自己触媒反応が支配的になるのが、図 2 で見るより、 もっと反応が進行してから(z*X = 0.2 など)であるためと考えられます。 ともあれ式 \eqref{eq:rate_autox} を導くにあたっての大胆な仮定も含め、 もっとスマートで突っ込んだ議論ができればいいんですが・・・。
|
|
| (a) | (b) |
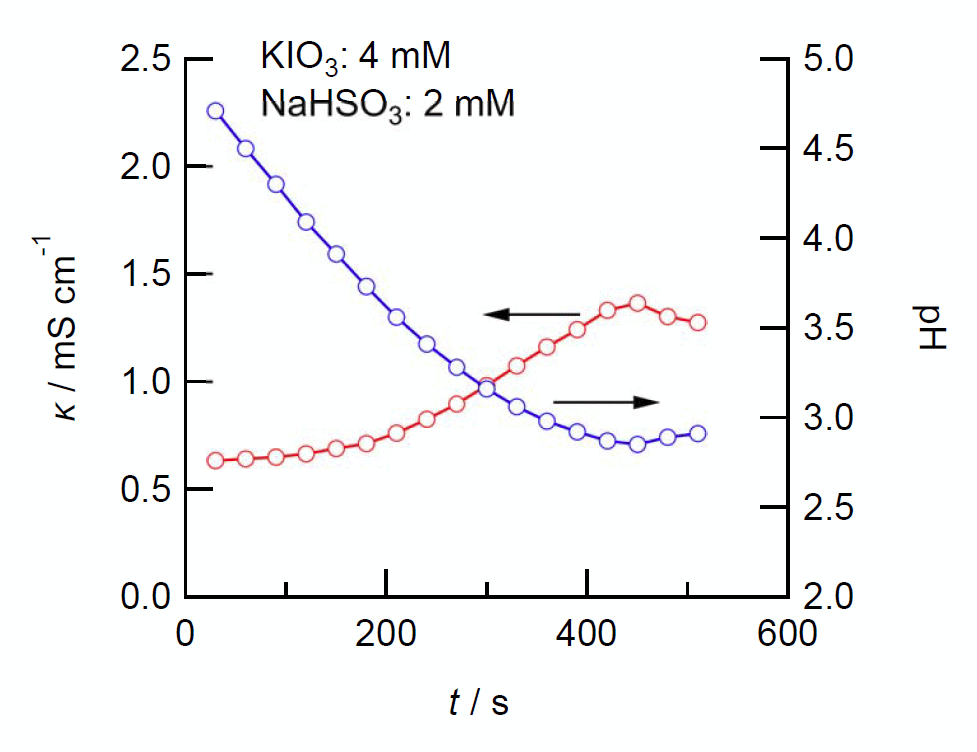
| 図 6. 電気伝導度 κ と pH の変化。 (a) は [KIO3]0 =2.0 mmol/L, [NaHSO3]0 = 4.0 mmol/L, (b) は [KIO3]0 =4.0 mmol/L, [NaHSO3]0 = 2.0 mmol/L での実験。 共に電気伝導度の極大になるところで pH が極小を示し、 ヨウ素の発色が観察されます。 | |
この節の最後に、以前、キンヒドロンの実験を行っていたころ、 学生さんたちと酸化還元電位(ORP)の変化を調べてみた結果を紹介しておきましょう。 実験はヨウ素酸カリウムと硫酸水素ナトリウムの濃度が同じになる条件で行い、 酸化還元電位はお手軽な ORP メータ(図 7a。HANNA HI-98120「高機能 ORP/°C テスター」)を用いて測っています (電位は Ag/AgCl に対するものが表示され、電極は白金のようです)。
興味深いのは、 ヨウ素による発色が現れるのに先んじて ORP の急上昇が現れることです。 ORP メータでどのような酸化還元反応の電位を検知しているかは難しいところですが、 I3-/3 I- の還元反応を想定すると、 図 7b の3つのケースでは亜硫酸水素イオンがほぼ失われる時点で、 ヨウ化物イオンの濃度が [HSO3-]0/3 ≈ 1 mmol/L なので、 還元電位はおよそ次式のように表されます(Ag/AgCl に対して):
| E / V = 0.34 + 0.030 log [I3-]/[I-]3 ~ 0.6 + 0.03 log [I3-] | (18) |
ヨウ素(三ヨウ化物イオン I3-)が視認できるのは 0.1 mmol/L 程度ぐらいまでですが、 その時の電位は式 (18) からおよそ 0.5 V。 図 7b で発色が観測される電位と合致します。 一方、実験的に急速に ORP が上昇しているのは 0.4 V ぐらいで、 発色が確認される1分ほど前にヨウ素の生成が 0.1 ~ 1 μmol/L ぐらいのオーダーで急速に起きていることになります。 ここまで誘導時間として見てきた、 ヨウ素の色が出現し pH や電気伝導度変化が反転する時点は、 亜硫酸水素イオンが反応し尽くした時点と見なしてよいものです。 一方 ORP が急上昇している時点は、 亜硫酸水素イオンがまだ残っているものの、 ヨウ素がわずかだが現れた状況ということになるでしょう。 このあたりは誘導時間というものをどう考えるかとも関わって、興味深いところです。
| d xA/d t = k xC - k xA | (19a) |
| d xB/d t = k xA - k xB | (19b) |
| d xC/d t = k xB - k xC | (19c) |
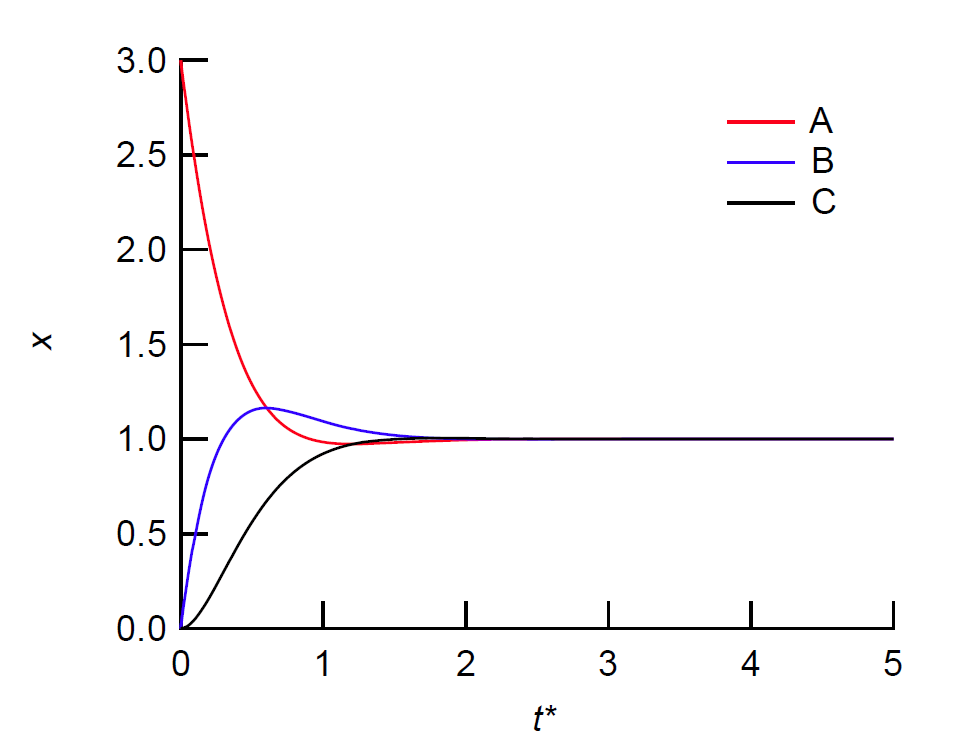
ここで k は速度定数です。 この反応系は、最終的に xA = xB = xC という平衡状態に達しますが、 その道のりは単純ではありません。 図 9a に、xA = 3、xB = xC = 0、 という条件から出発して平衡状態に至る、 A、B、C それぞれの物質量の変化を示しました。 簡単のため t* = kt としています。 A、B、C ともに平衡値 1 に収斂していくのですが、それぞれに様相がちがっています。 A の量は急速に減少していき、平衡値を若干下回った後増加に転じます。 B は最初、大きく増加した後、平衡値上回った後減少に転じます。 C は最初の増加は緩やかですが、その後順調に増加を続けます。 こうした挙動は興味深いものの、 ここからは振動的な挙動はちょっと見て取れません。
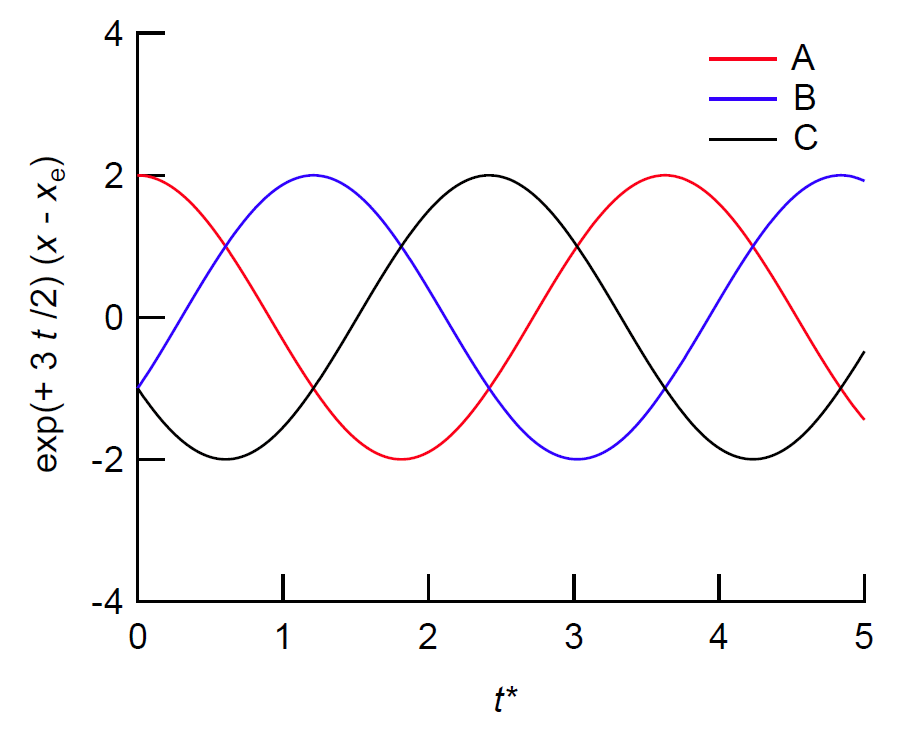
けれどもこれを平衡値からの偏倚(x - xe = x - 1)に注目し、 拡大してみると、図 9b のように(e+1.5 kt 倍しています)、 振動的な振る舞いが存在しています。 注意してみてもらうと、図 9a で xA、xB、xC の大小関係が、最初 xA > xB > xC だったのが時間経過とともに、 xB > xA > xC、 xB > xC > xA … と変わっているのがわかるでしょう。 それが図 9b ではあからさまに見えているわけです。 けれどもそうした挙動は、時間とともに指数関数的に減少(減衰)していくので、 図 9a では振動と見えないのです。 いずれ平衡に近づくというのは熱力学の言うところですが、 その近づき方にはいろいろなシナリオがあり、 ここで見た減衰振動も一つのシナリオです。 それを「化学振動」として歴然と見せるには、 先の時計反応でみた自己触媒反応のような、 増幅過程が必要となります。 無論、それだけで化学振動が起きるわけではありませんが・・・
|
|
| 図 9a. 図 8 のモデル反応系での、A、B、C の物質量 x の変動の様子。 t = 0 で、 xA = 3、xB = xC = 0 としています。 t* = kt です。 | 図 9b. 図 9a で平衡値からの偏倚(x - xe = x - 1) に注目し、e+1.5 kt 倍したものです。 振動的な挙動が存在し、図 9a の挙動が減衰振動であることが分かります。 |
\begin{eqnarray} x_{\mrm{A}}(t) &=& 1 + 2 \rme^{-3t/2} \cos \sqrt{3} t/2 \tag{XA} \\ x_{\mrm{B}}(t) &=& 1 + \rme^{-3t/2} \left( -\cos \sqrt{3} t/2 + \sqrt{3} \sin \sqrt{3} t/2 \right) \tag{XB} \\ x_{\mrm{C}}(t) &=& 1 + \rme^{-3t/2} \left( -\cos \sqrt{3} t/2 - \sqrt{3} \sin \sqrt{3} t/2 \right) \tag{XC} \end{eqnarray}
解の重ね合わせができるので、他の初期値でも同様の減衰振動の挙動が得られます。なお図 8 の化学反応系は微視的可逆性の原理を満たしていません。 微視的可逆性を要請すると、図 9b で見た振動的な挙動はなくなります。 このあたりは理屈好きの人にはたまらないところのようです。

|
| 図 10. 振動反応には3種類の試薬の混合が必要。 それぞれに 1 ml のディスポのスポイトを用意し、 混乱が起きないように色分けしてあります。 右方のトレイにはフェロイン溶液を入れたスポイト瓶 (油さし(オイラー)を流用)とルテニウム錯体溶液のサンプル瓶、 そしてこの時のお楽しみ課題だった、タンニン酸を用いた振動反応用の試薬が入っています。 |
実験に当たって、 必要試薬は図 10 のように用意して、全グループで分け取るようにしてもらっています。 テキストにあるように溶液はすべて 1 mol/L(2 N)硫酸溶液の形で提供しています。 これは溶液調整の手間を省いたためで(多分普通はセリウム溶液に硫酸濃度を 3 mol/L ぐらいにしているでしょう)、 このため臭素酸カリウム溶液は強酸性になって還元されやすく、 臭素の褐色を帯びていますが、 化学振動を起こす上では問題ありません(写真の試薬溶液は前年に調製して、冷蔵庫で保管していたもの)。 むしろ最初の誘導時間が短くなって好都合です (通常はマロン酸の溶液に臭化カリウム KBr を加えておくのですが、 これを省略しています)。
試薬を混合して、振動が起きるまで少し時間がかかります。 二酸化炭素の発泡が始まると、まもなく振動も始まります (BZ 反応は振動の起きるパラメータ領域が広く、少々混合比が違っても振動が起きます)。 何も指示薬を入れなくても、色の変動は分かりますが(セリウムの Ce(IV)(黄色)と Ce(III)(無色))、 フェロイン(鉄(II) のフェナントレン錯体 [Fe(phen)3]2+。 3回生の光吸収の実験で使用するのでフェナントレンの在庫が結構あり、 モール塩と混ぜてフェロイン溶液は自作しています。濃度は 0.01 mol/L で調製)を加えておくと、 赤と青の変化でより明瞭になります (図 11b)。 フェロインの標準還元電位 [Fe(phen)3]3+/[Fe(phen)3]2+ は 1.1 V ぐらいで、 Fe(II) では赤、Fe(III) では青を示します (セリウムの Ce(IV)/Ce(III) の標準還元電位は 1.72 V)。 振動の様子が分かりやすいように、さまざまな手法が知られており、 ルテニウムのビピリジン錯体 [Ru(bpy)3]2+ の蛍光を使う手法は、 ちょっと神秘的な感じで面白いので、 興味のある学生さんにはやってもらっています(図 11c)。 ルテニウムのビピリジン錯体の標準還元電位 [Ru(bpy)3]3+/[Ru(bpy)3]2+ は 1.24 V でフェロイン同様の酸化還元反応が期待でき、 蛍光を示す Ru(II) と 無蛍光の Ru(III) の間の変化が観察されます (ルテニウムのビピリジン錯体は光合成反応のモデル物質として有名です。 ここで使っているルテニウム錯体は、とある研究室からの放出品です)。
| 図 11a. フェロインを加えた化学振動の様子。 振動が始まるまで、数分、10 分ぐらい待つこともあります。 気泡が発生していることにも注意してください。 | 図 11b. フェロインを加えたもの(左手前)と加えないもの(右奥)の化学振動の様子。 フェロインを加えなくとも、無色と黄色の交代で、振動のようすは分かります。 このケースではフェロインの赤への変色は図 11a ほど鮮明ではありません。 | 図 11c. ルビジウムのビピリジン錯体を指示薬にした場合の BZ 反応。 赤い蛍光の有無で振動を検知します。 励起光は 400 nm ぐらいのランプで十分です。 |
なおこの実験で溶液の攪拌は重要です。 少しの温度の差などで振動の周期がずれると、 場所による色むらができて、色の変動が判然としない状態になったりします。 シャーレのような平たい容器に広げると、 こうして変化の様子がきれいに展開されたりするのですが(図 12)、 試験管などではうまくいきません。
ここでは元祖ベロウソフ-ザボチンスキー(BZ)反応を取り上げていますが、 化学振動反応を実施する立場からいうと、 ブリッグズ・ラウシャー Briggs-Rauscher(BR)反応の方が強酸性溶液を扱う必要がないので楽です (こぼして服についてもあまり心配なし。ただし過酸化水素には注意)。 以前、高校の文化祭でやってみたかったという学生さんが、 科学クラブの先輩から受け継いだという実験のメモを教えてくれたので、 その通りにやってみたことがありました。 メモの手法は Shakhashiri の "Chemical Demonstrations" 所載の手順(Procedure A)をなぞったものになっています。 スケールはほぼ 1/10 にしてあって、下記の A、B、C 3種類の溶液を調製し、それぞれ等量混合し、デンプン溶液を数滴加えます。
この反応の模様を図 12a に示します。 振動は混合して数分もたたないうちに速やかに起き、 振動の周期も 10 ~ 20 秒というところで BZ 反応より短く、 ちょっとやってみる分には飽きさせません。 振動の持続時間は BZ 反応より短いですが、20 分ぐらいは持ちます。 また変色の際に、 ヨウ素デンプンの藍色ではなくヨウ素の薄黄色(黄金色。図 12b)が現れて、 振動に色を添えたりしてくれることがあります。 ただ反応が終わった後、ヨウ素の沈殿ができてヨウ素臭いのはちょっと残念か(図 12b)。 これはこれで趣きがありますが・・・

| |
| 図 12a. ブリッグズ・ラウシャー(BR)反応の様子。 ヨウ素デンプン反応の藍色が、現れたり消えたりしています。 | 図 12b. BR 反応が終息した時点の様子。 ヨウ素デンプン反応の藍色の呈色はなくなり、 ヨウ素の褐色の溶液となり、ヨウ素の沈殿ができています。 |
ブリッグズ・ラウシャー(BR)反応はやって見る分には興味深いのですが、その内実はかなり複雑です。 元になっているのはヨウ素酸を触媒とする過酸化水素の分解反応の振動的な挙動(Bray 1921)ですが、 ここにベロウソフ-ザボチンスキー(BZ)反応の役者(マロン酸とセリウム改めマンガン)に共演願う形になっているからです。 このあたりが、学生実験で正規の課題として取り上げるのをためらわせるところです。
| 図 13. タンニン酸の臭素酸による酸化にともなう化学振動の様子。 フェロインを添加しています。 |
なおここまでは3種の溶液の混合を必要とする振動反応ですが、 2種の溶液の混合で振動する系も知られています。 実験を実施する上では、操作が単純で、混ぜる溶液の種類が少ないに越したことはありません。 Shakhashiri の "Chemical Demonstrations" に紹介されていますが、 タンニン酸の臭素酸による酸化にともなう化学振動を試みていたこともありました。 タンニン酸は麗々しく、没食子酸(3,4,5-トリヒドロキシ安息香酸)のエステルの形で分子式が与えられたりしていることがありますが、 実のところは、水によく溶けるタンニン(ポリフェノール)と言ってよいもののようです (薬局方では「通例、五倍子又は没食子から得たタンニンである」とされています)。
タンニン酸 1.3 mass% の溶液 2 mL に、4.0 mol/L の硫酸に臭素酸カリウム KBrO3 を濃度が 0.17 mol/L になるように溶かした溶液 2 mL を加えると、最初タンニン酸の沈殿ができます。 そこにフェロイン溶液を数滴加え、攪拌しながら観察していると、 図 13 のような振動が観察できます ( Shakhashiri の "Chemical Demonstrations" では臭化カリウム KBr も加えることになっていますが、 加えなくても化学振動は起きました)。 振動は 30 分ぐらい続き、最後、溶液は透明になっていきます。
この化学振動はあまり安定に起きないのが問題で、 同じように試薬を加えても振動しないケースがありました。 振動の起きるパラメータ領域がかなり狭いようです。 また何より溶液が濁っていて、あまり美しくありません。 ただ BZ 反応などで、セリウム塩(あるいはマンガン塩)を加えるわけですが、 それが必要不可欠というわけではないことを教えてくれている点で有意義かと思います。